Основные формулы комбинаторики

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно со­ставить из элементов, безразлично какой природы, задан­ного конечного множества. При непосредственном вычис­лении вероятностей часто используют формулы комбина­торики.

Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возмож­ных перестановок

Р_п = п!

Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

Р₈ = 3!= 1.2-3 = 6.

Размещениями называют комбинации, составленные из п различных элементов по т элементов, которые от­личаются либо составом элементов, либо их порядком. Число всех возможных размещений

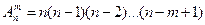
Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

Решение. Искомое число сигналов

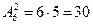
Сочетаниями называют комбинации, составленные из п различных элементов по т элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний

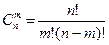
Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов

 

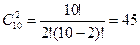
Число упорядоченных выборок с возвращением из п по к

п^к

Число упорядоченных выборок без возвращения из п по к

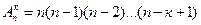, при п = к  – п!

Число неупорядоченных выборок без возвращения из п по к

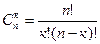
Число неупорядоченных выборок с возвращением из п по к

 

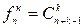
При решении задач комбинаторики используют сле­дующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов т способами, а другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т + п способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов т способами и после каждого такого выбора объект В можно выбрать п спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.

 

 

Примеры непосредственного вычисления вероятностей

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим через А событие — набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует собы­тию А лишь один исход (нужная цифра лишь одна). Искомая веро­ятность равна отношению числа исходов, благоприятствующих со­бытию, к числу всех элементарных исходов:

Р(А)=1/10.

Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их на­удачу. Найти вероятность того, что набраны нужные цифры.

Решение. Обозначим через В событие — набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. А²₁₀= 10×9 = 90. Таким образом, общее число возможных элементар­ных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благо­приятствующих событию, к числу всех элементарных исходов:

Р (А) = 1/90.

Пример 3. Указать ошибку «решения» задачи: «Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие А)».

Решение. Всего возможны 2 исхода испытания: сумма выпав­ших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход; общее число исходов равно двум. Сле­довательно, искомая вероятность

Р (А) = 1/2.

Ошибка этого решения состоит в том, что рассматриваемые ис­ходы не являются равновозможными.

Правильное решение. Общее число равновозможных ис­ходов испытания равно 6×6 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность

Р(А) = 3/36 =1/12.

Пример 4. В партии из 10 деталей 7 стандартных. Найти вероят­ность того, что среди шести взятых наудачу деталей 4 стандартных.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. числу сочетаний из 10 элементов но 6 элементов (C⁶₁₀).

Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых детален 4 стандартных). Четыре стандартные детали можно взять из семи стандартных деталей С⁴₇ спо­собами; при этом остальные 6—4 = 2 детали должны быть нестан­дартными; взять же 2 нестандартные детали из 10 — 7 = 3 нестандарт­ных деталей можно способами. Следовательно, число благоприя­тствующих исходов равно С⁴₇ × С²₃

Искомая вероятность раина отношению числа исходов, благо­приятствующих событию, к числу всех элементарных исходов:

Р(А) = С⁴₇ × С²₃/ C⁶₁₀  =1/2

 

Контрольные вопросы

1. Что является предметом теории вероятностей?

2. Что такое «испытание»?

3. Что такое «событие»?

4. Что такое «случайное событие»?

5. Что такое «вероятность события»?

6. В чем заключается статистическое определение вероятности?

7. При каких условиях можно применять классическое определение вероятности?

8. Какова формулировка классического определения вероятности?

9. Приведите несколько примеров достоверных, невозможных и случайных событий.

10.Чему равна вероятность невозможного и достоверного событий?

11.Дайте определение суммы и произведения событий. Примеры.

12.Как понимают равенство двух событий? Примеры.

13.Какие события называют противоположными? Примеры.

14.Что обозначают слова “наугад”, ”произвольно”? Примеры.

15.Что такое перестановки? Число всех возможных перестановок?

16.Что такое размещение? Число всех возможных размещений?

17.Что такое сочетания? Число всех возможных сочетаний?

18.В чем заключается «правило суммы»?

19.В чем заключается «правило произведения»?

 

Лекция № 2

Тема: «Теорема сложения и умножения вероятностей»

План лекции

1. Сумма и произведение событий.

2. Теорема сложения вероятностей.

3. Понятие условной вероятности.

4. Теорема умножения вероятностей.

5. Решение задач.

 

Теорема сложения вероятностей несовместных событий

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из ору­дия произведены два выстрела и А — попадание при пер­вом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при вто­ром, или в обоих выстрелах.

В частности, если два события А и В—несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, кото­рое состоит в появлении хотя бы одного из этих собы­тий. Например, событие А + В + С состоит в появлении одного из следующих событий: А; В; С; А и В; А и С; В и С; А и В и С.

Пусть события А и В—несовместные, причем вероят­ности этих событии известны. Как найти вероятность того, что наступит либо событие А, либо событие В? Ответ на этот вопрос дает теорема сложения.

Теорема. Вероятность появления одного из двух несов­местных событий, безразлично какого, равна сумме веро­ятностей этих событий:

Р(А + В) = Р(А) + Р(В).

Следствие. Вероятность появления одного из не­скольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A_l + A₂+... + A_п) = P(A₁) + P(A₂)+...+P(A_п).

Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие А)

Р(А) =10/30= 1/3.

Вероятность появления синего шара (событие В)

Р(В) = 5/30= 1/6.

События А и В несовместны (появление шара одного цвета исклю­чает появление шара другого цвета), поэтому теорема сложения при­менима.

Искомая вероятность

Р(А + В) = Р(А) + Р(В) = 1/3 + 1/6 = 1/2.

Пример 2. Стрелок стреляет по мишени, разделенной на 3 об­ласти. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Решение. События А — «стрелок попал в первую область» и В — «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность

Р (А + В) = Р (А) + Р(В) = 0,45 + 0,35 = 0,80.

 

Полная группа событий

Теорема. Сумма вероятностей событий А₁, А₂, ..., А_п, образующих полную группу, равна единице:

P (A_l + A₂+... + A_п) = P(A₁ ) + P(A₂)+...+P(A_п) = 1

Пример. Консультационный пункт института получает пакеты с контрольными работами из городов А, В к С. Вероятность полу­чения пакета из города А равна 0,7, из города В — 0,2. Найти веро­ятность того, что очередной пакет будет получен из города С.

Решение. События «пакет получен из города А», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице:

0,7 + 0,2 + p =l. Отсюда искомая вероятность

р = 1— 0,9 = 0,1.

 

Противоположные события

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать Ā.

Пример 1. Попадание и промах при выстреле по цели — противо­положные события. Если А — попадание, то Ā — промах.

Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противо­положные.

Теорема. Сумма вероятностей противоположных собы­тий равна единице:

Р(А) + Р(Ā)=1.

Замечание 1. Если вероятность одного из двух противопо­ложных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы

р + q = l .

Пример 3. Вероятность того, что день будет дождливым, р = 0,7. Найти вероятность того, что день будет ясным.

Решение. События «день дождливый» и «день ясный» — про­тивоположные, поэтому искомая вероятность

4 =1—р = 1—0,7 = 0,3.

Замечание 2. При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность события Ā, а затем найти искомую вероятность по формуле

Р(А) = 1 - Р(Ā).

Пример 4. В ящике имеется п деталей, из которых т стандарт­ных. Найти вероятность того, что среди k наудачу извлеченных дета­лей есть хотя бы одна стандартная.

Решение. События «среди извлеченных деталей есть хотя бы одна стандартная» и «среди извлеченных деталей нет ни одной стан­дартной» - противоположные. Обозначим первое событие через А, а второе—через Ā,

Очевидно,

Р(А) = 1 - Р(Ā).

Найдем Р (Ā). Общее число способов, которыми можно извлечь к деталей из п деталей, равно Число нестандартных деталей равно п—т; из этого числа деталей можно С^к_п-т способами извлечь к не­стандартных деталей. Поэтому вероятность того, что среди извлечен­ных к деталей нет ни одной стандартной, равна Р (Ā)= С^к_п-т / С^к_п.

Искомая вероятность

Р (А) =1 -Р (Ā) = 1 - С^к_п-т / С^к_п.

 

Теорема умножения вероятностей

Произведение событий

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совме­щении) этих событий. Например, если А—деталь годная, В—деталь окрашенная, то АВ—деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С—появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то ABC — выпадение «герба» во всех трех испытаниях.

Условная вероятность

Во введении случайное событие определено как событие, которое при осуществлении совокупности усло­вий S может произойти или не произойти. Если при вы­числении вероятности события никаких других ограни­чений, кроме условий S, не налагается, то такую вероят­ность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность собы­тия В при дополнительном условии, что произошло со­бытие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S.

Условной вероятностью Р_А(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило, и по определению, равна

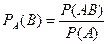, (Р (А) > 0).

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероят­ность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

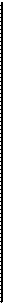
Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность

Ра(В) =3/5. Этот же результат можно получить по формуле

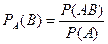, (Р (А) > 0).                                       

Действительно, вероятность появления белого шара при первом ис­пытании      

Р (А) = 3/6 = 1/2.

Найдем вероятность Р(АВ) того, что в первом испытании по­явится черный шар, а во втором—белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений А²₆= 6 ∙ 5 = 30. Из этого числа исходов событию АВ благоприятствуют 3 ∙ 3 = 9 исходов. Следовательно,

Р(АВ) =9/30 = 3/10. Искомая условная вероятность

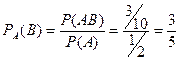
Как видим, получен прежний результат.

 

Теорема умножения вероятностей

Рассмотрим два события: А и В; пусть вероят­ности Р(А) и Р_а(В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.

Теорема. Вероятность совместного появления двух со­бытий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предпо­ложении, что первое событие уже наступило:

Р(АВ) = Р(А)Р_А(В) или Р(АВ) = Р(В)Р_В(А).

 

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появи­лись: для трех событий

 

Р(АВС) = Р(А)Р_А(В)Р_АВ(С).

 

Заметим, что порядок, в котором расположены собы­тия, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д.

Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероят­ность того, что первый из взятых валиков —конусный, а второй — эллиптический.

Решение. Вероятность того, что первый валик окажется ко­нусным (событие А),

Р (А) =3/10.

Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность

Р_А (В) = 7/9.

По теореме умножения, искомая вероятность

Р (АВ)=Р (А)Р_А (В) = (3/10) ∙ (7/9) = 7/30.

Заметим, что, сохранив обозначения, легко найдем: Р (В) = 7/10, Рв (А) = 3/9,

Р (В) Р_В (А) = 7/30, что наглядно иллюстрирует спра­ведливость равенства.

 

Пример 2. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не воз­вращая его обратно. Найти вероятность того, что при первом испы­тании появится белый шар (событие А), при втором — черный (собы­тие В) и при третьем—синий (событие С).

Решение. Вероятность появления белого шара в первом испытании

Р (А) = 5/12.

Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность

Р_А (В) = 4/11.

Вероятность появления синего шара в третьем испытании, вы­численная в предположении, что в первом испытании появился белый шар, а во втором—черный, т. е. условная вероятность

Р_АВ(С) = 3/10.

Искомая вероятность

Р (ABС) =Р (А) Р_А (В) Р_АВ (С) = (5/12) ∙ (4/11) ∙ (3/10) = 1/22.

 

Независимые события. Теорема умножения для независимых событий

 

Пусть вероятность события В не зависит от по­явления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

Р_А(В) = Р(В) или Р_В(А) = Р(А),

т. е. условная вероятность события А в предположении, что наступило событие В, равна его безусловной вероят­ности. Другими словами, событие А не зависит от со­бытия В.

Итак, если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения Р (АВ) = Р (А) Р_А (В) имеет вид

Р(АВ) = Р(А)Р(В),

т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависи­мыми.

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» неза­висимы.

Пример 1. Имеется 3 ящика, содержащих по 10 деталей. В пер­вом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти веро­ятность того, что все три вынутые детали окажутся стандартными.

Решение.

Вероятность того, что из первого ящика вынута стандартная деталь (событие А),

Р (А) = 8/10 = 0,8.

Вероятность того, что из второго ящика вынута стандартная деталь (событие В),

Р (В) = 7/10 = 0,7.

Вероятность того, что из третьего ящика вынута стандартная деталь (событие С),

Р (С) =9/10 = 0,9.

Так как события А, В и С независимые в совокупности, то ис­комая вероятность (по теореме умножения) равна

Р (ABC) = Р (А) Р (В) Р (С) = 0,8 ∙ 0,7 ∙ 0,9 = 0,504.

Приведем пример совместного применения теорем сложения и умножения.

Пример 4. Вероятности появления каждого из трех независимых событий А₁, А₂, А₃ соответственно равны p_l,  р₂, Р₃. Найти вероят­ность появления только одного из этих событий.

Решение. Заметим, что, например, появление только первого события A₁ равносильно появлению события А₁Ā₂Ā₃ (появилось пер­вое и не появились второе и третье события). Введем обозначения:

В₁ — появилось только событие А₁, т. е. В₁ = А₁Ā₂Ā₃;

В₂— появилось только событие А₂, т. е. В₂ = А₂Ā₁Ā₃;

В₃ — появилось только событие А₃, т. е. В₃=А₃Ā₁Ā₂.

Таким образом, чтобы найти вероятность появления только одного из событий А₁, А₂, А₃, будем искать вероятность Р (В₁ + В₂ + В₃) появления одного, безразлично какого из событий B₁, B₂, В₃.

Так как события В₁, В₂, В₃ несовместны, то применима теорема сложения

Р (В₁ + В₂+ В₃) = P (В₁)+Р (В₂) + Р (В₃).

Остается найти вероятности каждого из событий B₁, B₂, В₃.

События А₁, А₂, А₃ независимы, следовательно, независимы события A_l,  Ā₂, Ā₃, поэтому к ним применима теорема умножения

Р (В₁) =P (A_lĀ₂Ā₃) =Р (A₁) Р (Ā₂) Р (Ā₃) = р_lq₂q₃. Аналогично,

Р (В₂) =Р(А₂Ā₁Ā₃) = Р (А₂) Р (Ā₁) Р (Ā₃) = p₂q₁q₃;

Р (В₃) = Р(А₃Ā₁Ā₂)= Р(А₃) Р (Ā₁) Р (Ā₂) = р₃q₁q₂.

Найдем искомую вероятность появ­ления только одного из событий A_l, А₂, А₃:

Р (В₁ + В₂ + В₃) = р₁q₂q₃ + p₂q₁q₃ + р₃q₁q₂.

---

Дата добавления: 2019-09-13; просмотров: 208; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!