Вероятность появления хотя бы одного события

 

Пусть в результате испытания могут появиться п событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий A ₁ , A ₂ , ..., А_п, независимых в совокупности, равна разности между единицей и произведением вероят­ностей противоположных событий Ā₁, Ā₂, ..., Ā_п:

P ( A )= 1 — q ₁ q ₂ ... q_n .

Частный случай. Если события A ₁ , A ₂ , ..., А_п имеют одинаковую вероятность, равную р, то вероят­ность появления хотя бы одного из этих событий

P ( A ) = 1 — qⁿ .

Пример 1. Вероятности попадания в цель при стрельбе из трех орудии таковы: р₁ = 0,8; р₂ = 0,7; р₃ = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рас­сматриваемые события А₁ (попадание первого орудия), А₂ (попадание второго орудия) иА₃ (попадание третьего орудия) независимы в со­вокупности.

Вероятности событий, противоположных событиям А₁, A₂ и A₃ (т. е. вероятности промахов), соответственно равны:

q₁ = l - р₁ =1- 0,8 = 0,2; q₂ = l – р₂ = 1-0,7 = 0,3; q₃ = l – р₃ = 1—0,9 = 0,1.

Искомая вероятность

Р (А) = 1 - q₁q₂q₃= 1 —0,2∙0,3∙0,1 =0,994.

 

Пример 2. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не рабо­тает» (в данный момент)—противоположные, поэтому сумма их веро­ятностей равна единице:

р + q=l.

Отсюда вероятность того, что машина в данный момент не работает равна

q=1—р = 1—0,9 = 0,1. Искомая вероятность

Р(А) = 1 — qⁿ = 1 -0,1⁴=0,9999.

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности мало­вероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

 

Пример 3. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы един раз». События, состоящие в попадании в цель при первом, втором выстрелах и т.д., независимы в совокупности, поэтому применима формула

Р(А) = 1 — qⁿ

Приняв во внимание, что, по условию, Р(А)≥0,9, р=0,4

1—0,6^п ≥0,9; отсюда 0,6^п ≤ 0,1.

Прологарифмируем это неравенство по основанию 10:

nlg0,6≤lg0,l.

Отсюда, учитывая, что lg0,6 < 0, имеем

п ≥ lg 0,1/lg 0,6 =—1/1,7782 =—1/(—0,2218) = 4,5.

Итак, n=5, т. е. стрелок должен произвести не менее 5 вы­стрелов.

 

Пример 4. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании (предпо­лагается, что во всех испытаниях вероятность появления события одна и та же).

Решение. Так как рассматриваемые события независимы в совокупности, то применима формула

Р(А) = 1 — qⁿ

По условию, Р (А) =0,936; п = 3. Следовательно,

0,936=1 —q ³ или q³= 1—0,936 = 0,064.

Отсюда 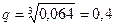 Искомая вероятность

р =1— q =1—0,4 = 0,6.

 

Контрольные вопросы.

1. Что такое множество элементарных событий?

2. Что такое сумма случайных событий?

3. Что такое произведение случайных событий?

4. Что такое разность событий?

5. Что такое множество случайных событий?

6. Что такое противоположное событие?

7. Что такое несовместные события?

8. Какова вероятность суммы двух совместных событий?

9. Какие события образуют полную группу?

10. Какова вероятность противоположного события?

11. Что такое условная вероятность?

12. Как выражается условная вероятность через безусловную?

13. Как связаны условные вероятности двух независимых событий?

14. Какова формула произведения событий?

15. Чему равна вероятность появления хотя бы одного события из независимых в совокупности событий?

 

Лекция № 3

 

Тема: «Формула полной вероятности. Теорема Бейеса»

План лекции

1. Формула полной вероятности

2. Вероятность гипотез. Формулы Бейеса

3. Решение задач.

 

Формула полной вероятности

Пусть событие А может наступить при условии появления одного из несовместных событий B_1, В₂,..., В_n, которые образуют полную группу. Пусть известны веро­ятности этих событий и условные вероятности Рв₁(А), Рв₂(А) , …, Рв_n(А) события А. Как найти вероятность событияA? Ответ на этот вопрос дает следующая теорема.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несо­вместных событий B_l, B₂, ..., В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероят­ность события А:

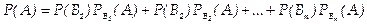
Эту формулу называют «формулой полной вероятности».

 

Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго—0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) — стандартная.

Решение. Обозначим через А событие «извлеченная деталь стандартна».

Деталь может быть извлечена либо из первого набора (собы­тие В₁), либо из второго (событие В₂).

Вероятность того, что деталь вынута из первого набора, Р(В₁) = 1/2.

Вероятность того, что деталь вынута из второго набора, Р(В₂) = 1/2.

Условная вероятность того, что из первого набора будет извле­чена стандартная деталь, Pв₁(A)=0,8.

Условная вероятность того, что из второго набора будет извле­чена стандартная деталь, Pв₂(A)=0,9.

Искомая вероятность того, что извлеченная наудачу деталь - стандартная, по формуле полной вероятности равна

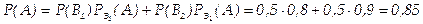
Пример 2. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке—10 ламп, из них 9 стандарт­ных. Из второй коробки наудачу взята лампа и переложена в пер­вую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.

Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа».

Из второй коробки могла быть извлечена либо стандартная лампа (событие B₁), либо нестандартная (событие B₂).

Вероятность того, что из второй коробки извлечена стандартная лампа, Р (В₁) =9/10.

Вероятность того, что из второй коробки извлечена нестандарт­ная лампа, Р (В₂) = 1/10.

Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна Pв_l(A)= 19/21.

Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна Рв₂(А)=18/21.

Искомая вероятность того, что из первой коробки будет извле­чена стандартная лампа, по формуле полной вероятности равна

 

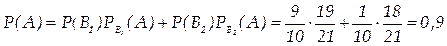
Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий B_1, В₂,..., В_n, образующих полную группу. Поскольку заранее не из­вестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А опреде­ляется по формуле полной вероятности:

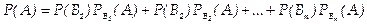
Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что собы­тие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

Р_А(В₁), Р_А(В₂),…, Р_А(В_n),

Условная веро­ятность любой гипотезы В_і (i = 1, 2, ..., n) может быть вычислена по формуле

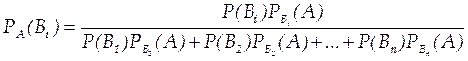
Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как ста­новится известным результат испытания, в итоге кото­рого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Веро­ятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет приз­нана стандартной первым контролером, равна 0,94, а вторым — 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предполо­жения:

1) деталь проверил первый контролер (гипотеза В₁);

2) деталь проверил второй контролер (гипотеза В₂).

Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:

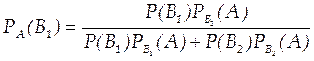
По условию задачи имеем:

Р(В₁) = 0,6 (вероятность того, что деталь попадает к первому конт­ролеру);

Р (В₂) = 0,4 (вероятность того, что деталь попадет ко второму конт­ролеру);

Рв₁(А) = 0,94 (вероятность того, что годная деталь будет признана первым контролером стандартной);

Р в₂ (А) = 0,98 (вероятность того, что годная деталь будет признана вторым контролером стандартной).

Искомая вероятность

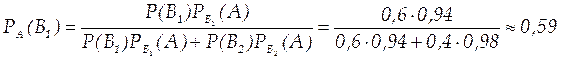
Как видно, до испытания вероятность гипотезы В₁ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала рав­ной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.

 

Контрольные вопросы.

1. Каковы условия задачи, определяемой формулой полной вероятности?
2. Напишите формулу полной вероятности
3. Каковы условия задачи, определяемой формулой Бейеса?
4. Напишите формулу Бейеса.
5. Что такое множество случайных событий?
6. Что такое противоположное событие?
7. Что такое несовместные события?
8. При каких условиях можно применять классическое определение вероятности?
9. Какова формулировка классического определения вероятности?
10. Как понимают равенство двух событий? Примеры.
11. Какие события называют противоположными? Примеры.

 

 

Лекция № 4

Тема: «Повторение испытаний»

План лекции

1. Формула Бернулли

2. Локальная теорема Лапласа

3. Интегральная теорема Лапласа

 

Формула Бернулли

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Формула Бернулли. Вероятность одного слож­ного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п— k раз, по теореме умножения вероятностей независимых событий равна p^kq^{n - k}. Таких сложных событий может быть столько, сколько можно составить сочетаний из п эле­ментов по k элементов, т. е. С^к_п. Так как эти сложные события несовместны, то по теореме сложения вероятно­стей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз со­бытия А в п испытаниях) равна вероятности одного сложного события, умноженной на их число:

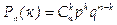
Полученную формулу называют формулой Бернулли.

Пример. Вероятность того, что расход электроэнергии в продол­жение одних суток не превысит установленной нормы, равна р= 0,75. Найти вероятность того, что в ближайшие 6 суток расход электро­энергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р=0,75. Сле­довательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 – р = 1- 0,75 = 0,25.

Искомая вероятность по формуле Бернулли равна

 

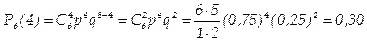
Локальная теорема Лапласа

Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испы­таний достаточно велико.

Заметим, что для частного случая, а именно для р = 1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому тео­рему, о которой здесь идет речь, иногда называют теоремой Муавра—Лапласа.

Локальная теорема Лапласа. Если вероятность р появ­ления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_п (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

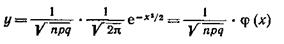
при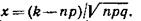

Имеются таблицы, в которых помещены значения функции 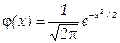, соответствующие положитель­ным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция φ(х) четна, т. е. φ (—х) = φ(х).

Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна

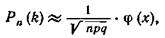
где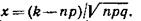

Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию, n = 400; к = 80; р = 0,2; q = 0,8. Вос­пользуемся асимптотической формулой Лапласа:

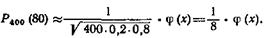
Вычислим определяемое данными задачи значение х:

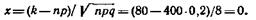
По таблице приложения 1 находим φ (0) = 0,3989. Искомая вероятность

Р₄₀₀ (80) = (1 /8) ∙ 0,3989 = 0,04986.

Формула Бернулли приводит примерно к такому же результату Р400 (80) =0,0498

Пример 2. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. По условию, п=10; к= 8; p=0,75; q = 0,25. Воспользуемся асимптотической формулой Лапласа:

Вычислим определяемое данными задачи значение х:

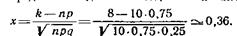
По таблице приложения 1 находим φ (0,36) = 0,3739. Искомая вероятность

Р₁₀ (8) = 0,7301 ∙ 0,3739 = 0,273.

Формула Бернулли приводит к иному результату, а именно Р₁₀ (8) =0,282. Столь значительное расхождение ответов объясняется тем, что в настоящем примере п имеет малое значение (формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п).

 

Интегральная теорема Лапласа

Вновь предположим, что производится п испы­таний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычис­лить вероятность Р_п ( k_x , k ₂ ) того, что событие А появится в п испытаниях не менее k ₁ и не более k ₂ раз (для крат­кости будем говорить «от k₁ до k₂ раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.

Теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_п ( k ₁ , k ₂ ) того, что событие А появится в п испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу

 

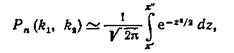
где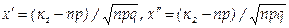

При решении задач, требующих применения интеграль­ной теоремы Лапласа, пользуются специальными табли­цами, так как неопределенный интеграл 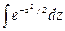 не выражается через элементарные функции. Таблица для интеграла 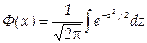приведена в методичке для самостоятельного изучения. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х<0 пользуются той же таблицей [функция Ф(х) нечетна, т.е. Ф(—х) = —Ф(х)]. В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф(х) часто называют функцией Лапласа.

Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразовывают соотношение

 

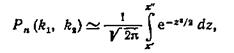
Итак, вероятность того, что событие А появится в п независимых испытаниях от k₁ до k₂ раз,

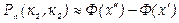
где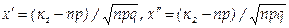

Приведем примеры, иллюстрирующие применение ин­тегральной теоремы Лапласа.

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно ото­бранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию, р = 0,2; q = 0,8; n = 400; k₁ = 70; k₂=100. Воспользуемся интегральной теоремой Лапласа:

Р₄₀₀ (70, 100) = Ф (x")-Ф (х'). Вычислим нижний и верхний пределы интегрирования:

 

Таким образом, имеем

Р₄₀₀(70, 100) = Ф(2,5) - Ф(-1,25) = Ф(2,5) + Ф(1,25). По таблице приложения 2 находим:

Ф (2,5) =0,4938; Ф (1,25) =0,3944. Искомая вероятность

Р₄₀₀ (70, 100) = 0,4938 + 0,3944 = 0,8882.

 

Контрольные вопросы.

1. Объясните условие независимых испытаний
2. Запишите формулу Бернулли
3. Сформулируйте локальную предельную теорему Муавра-Лапласа
4. Сформулируйте интегральную предельную теорему Муавра-Лапласа
5. Какова вероятность суммы двух совместных событий?
6. Какие события образуют полную группу?
7. Какова вероятность противоположного события?
8. Что такое условная вероятность?
9. Как выражается условная вероятность через безусловную?
10. Как связаны условные вероятности двух независимых событий?
11. Какова формула произведения событий?

 

Лекция № 5

Тема: «Виды случайных величин. Математическое ожидание и дисперсия»

План лекции

1. Случайная величина. Виды случайных величин

2. Закон распределения вероятностей дискретной случайной величины

3. Математическое ожидание дискретной случайной величины

4. Дисперсия дискретной случайной величины

5. Среднее квадратическое отклонение дискретной случайной величины

 

Случайная величина

Уже в первой части приводились события, со­стоящие в появлении того или иного числа. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа 1, 2, 3, 4, 5 и б есть возможные значения этой величины.

 Случайной называют величину, которая в результате испытания примет одно и только одно возможное значе­ние, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, ..., 100.

Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принад­лежат некоторому промежутку (а, Ь).

Будем далее обозначать случайные величины пропис­ными буквами X, Y, Z, а их возможные значения — соот­ветствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значе­ния, то они будут обозначены так: x₁, x₂, х₃.

---

Дата добавления: 2019-09-13; просмотров: 811; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!