Дискретные и непрерывные случайные величины

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

Вернемся к примерам, приведенным выше. В первом из них случайная величина X могла принять одно из следующих возможных значений: 0, 1, 2, ..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений X. Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. Во втором примере случайная величина могла принять любое из значений промежутка (а, Ь). Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.

Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Замечание. Настоящее определение непрерывной случайной величины не является точным. Более строгое определение будет дано позднее.

Закон распределения вероятностей дискретной случайной величины

На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их — различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично. Аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х	х₁	х₂	…	х_п
Р	р₁	р₂	…	р_п

События х₁, х₂, …, х_п образуют полную группу, следовательно, сумма вероятностей этих событий равна единицы.

Числовые характеристики дискретных случайных величин

Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных; числовых характеристик относится математическое ожидание.

Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическое ожидание дискретной случайной величины

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только значения х₁, х₂, ..., х_п, вероятности которых соответственно равны р₁, р₂, .. ., р_п. Тогда математическое ожидание М(X) случайной величины X определяется равенством

М(Х) = х₁р₁ + х₂р₂+...+х_пр_п.

Если дискретная случайная величина X принимает счетное множество возможных значений, то

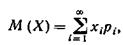
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Пример 1. Найти математическое ожидание случайной величины X, зная закон ее распределения:

Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

М (Х) = 3 ∙ 0,1 +5 ∙ 0,6 + 2 ∙ 0,3 = 3,9.

Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.

Решение. Случайная величина X— число появлений события А в одном испытании — может принимать только два значения: х₁= 1 (событие А наступило) с вероятностью р и х₂= 0 (событие А не наступило) с вероятностью q = 1—р. Искомое математическое ожидание

M(X) = l ∙ p + 0 ∙ q = p

Дата добавления: 2019-09-13; просмотров: 940; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!