Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку [0, 1]:

0 < F (х) < 1.

Свойство 2. F (х)—неубывающая функция, т. е. F (х₂) > F (х₁), если х₂ > х₁.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

P(a < X < b) = F(b)—F(a)

Пример . Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу (0, 2):

Р (0 < X < 2) = F (2) — F (0).

Решение. Так как на интервале (0, 2), по условию, F(x) = x/4 + l/4, то

F(2) - F(0) = (2/4+l/4) - (0/4 + l/4) = l/2. Итак,

Р(0< X <2) = 1/2.

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот фак полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером. Заметим, что было бы неправильным думать, что равенство нулю вероятности Р (X =х₁) означает, что событие Х=х₁ невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений; в частности, это значение может оказаться равным х₁.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, Ь), то: 1) F(х) = 0 при х ≤ а; 2) F(x) =l при х ≥ b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

График функции распределения

Доказанные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми у = 0, у=1 (первое свойство).

При возрастании х в интервале (а, Ь), в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство).

При х ≤ а ординаты графика равны нулю; при х ≥ b ординаты графика равны единице (третье свойство).

Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере

Пример. Дискретная случайная величина X задана таблицей распределения

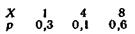
Найти функцию распределения и начертить ее график.

Решение. Если х ≤ 1, то F (х) = 0 (третье свойство).

Если 1≤ x ≤ 4, то F(x) = 0,3. Действительно, X может принять значение 1 с вероятностью 0,3.

Если 4 < х ≤ 8, то F (х) =0,4. Действительно, если х₁ удовлетворяет неравенству 4 <x₁≤8, то F(x₁) равно вероятности события X<х₁, которое может быть осуществлено,
когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события X<х₁ равна сумме вероятностей 0,3 + 0,1=0,4.

Если х > 8, то F(x) = l. Действительно, событие Х ≤ 8 достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

График этой функции приведен на рисунке

Дата добавления: 2019-09-13; просмотров: 162; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒

Мы поможем в написании ваших работ!