Вопросы к экзамену по дисциплине «Высшая математика»

(часть 3)

1. Определение случайной величины. Вероятностное пространство, образованное случайной величиной.

2. Функция распределения и ее свойства.

1. Дискретные случайные величины. Закон распределения дискретной случайной величины.

4. Непрерывные случайные величины. Плотность распределения вероятностей случайной величины. ЕЕ свойства.

5. Математическое ожидание и его свойства. Мода и медиана.

6. Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение.

7. Моменты распределения случайных величин. Асимметрия и эксцесс.

8. Биномиальное распределение. Числовые характеристики. Функция распределения.

9. Наивероятнейшее число появления событий в независимых испытаниях.

10. Распределение Пуассона. Простейший поток событий. Числовые характеристики. Функция распределения.

11. Геометрическое распределение. Числовые характеристики. Функция распределения.

12. Гипергеометрическое распределение. Числовые характеристики. Функция распределения.

13. Равномерное распределение. Его числовые характеристики. Функция распределения.

14. Нормальное распределение. Его числовые характеристики. Функция распределения. Вероятность попадания случайной величины, подчиненной нормальному закону распределения, на заданный интервал.

15. Показательное распределение. Его числовые характеристики. Функция распределения.

16. Неравенства Чебышева, Колмогорова.

17. Теорема Чебышева, Хинчина, Маркова.

18. Теоремы, устанавливающие связь между частью события и его вероятностью.

19. Центральная предельная теорема в формулировке Линдерберга-Леви, Ляпунова. Нормальное распределение как предельное для биномиального и пуассоновского распределения.

20. Предельные теоремы Муавра-Лапласа.

21. Вероятность отклонения относительной частоты от постоянной вероятности.

22. Генеральная совокупность. Выборка.

23. Распределение выборки. Графическое представление распределений.

24. Эмпирическая функция распределения и ее свойства.

25. Основные числовые характеристики выборки: среднее арифметическое, мода, медиана, стандартная ошибка, вариационный размах, среднее линейное отклонение, коэффициенты вариации, начальные и центральные моменты, асимметрия, эксцесс.

26. Точечное оценивание. Свойства точечных оценок. Оценки математического ожидания, дисперсии.

27. Метод наибольшего правдоподобия и метод моментов нахождения оценок параметров распределений.

28. Доверительный интервал и доверительная вероятность. Методы построения доверительных интервалов.

29. Доверительные интервалы для математического ожидания и для дисперсии нормально распределенной случайной величины.

30. Определение статистической гипотезы, критерия, ошибок первого и второго рода; определение критической области, мощности критерия; схема проверки статистической гипотезы.

31. Проверка гипотез о математическом ожидании и дисперсии случайной величины, распределенной по нормальному закону.

32. Проверка гипотез о равенстве математических ожиданий и дисперсий.

33. Критерии согласия Пирсона, Романовского, Колмогорова.

34. Построение законов распределения экономических процессов.

     Математическая запись задачи математического программирования.

35. Различные эквивалентные формы записи задачи линейного программирования.

36. Геометрическая интерпретация задачи линейного программирования. Графический метод решения.

37. Применение задач линейного программирования в экономических исследованиях: «Модель минимизации затрат на перевозку грузов» и другие модели.

38. Опорные планы задачи линейного программирования.

39. Основная теорема линейного программирования.

40. Сущность симплексного метода. Геометрическая интерпретация симплексного метода.

41. Построение начального опорного плана. Симплексные преобразования.

42. Признаки неограниченности целевой функции, неограниченности множества оптимальных планов.

43. Применение симплексного метода в экономических исследованиях: «Определение плана выпуска продукции, максимизирующего прибыль» и другие модели.

44. Понятие двойственности. Построение двойственных задач.

45. Соответствие между переменными пары взаимно двойственных задач.

46. Основное неравенство теории двойственности.

47. Достаточный признак оптимальности планов.

48. Теоремы существования оптимальных планов и их экономическая интерпретация.

49. Постановка задач целочисленного программирования:

общая задача о расписании, задача коммивояжера, задача о разбиении, покрытии и упаковке, задача о размещении оборудования, задача раскроя.

49. Методы ветвей и границ.

50. Методы отсечений.

51. Постановка задачи нелинейного программирования и ее геометрическая интерпретация. Метод множителей Лагранжа.

52. Выпуклое программирование. Задачи выпуклого программирования. Выпуклые и вогнутые функции. Теорема Куна-Таккера. Понятие о глобальном и о локальном оптимуме.

53. Квадратичное программирование.

54. Вычислительная схема метода динамического программирования.

55. Динамические задачи выбора наиболее экономичного маршрута доставки груза, оптимального распределения средств на расширение производства, определения оптимальной стратегии замены оборудования, формирования оптимальной программы производства с учетом запасов (в зависимости от специальности).

 

 

Вспомогательный раздел

ГЛОССАРИЙ

Матрица – прямоугольная таблица, состоящая из m – строк и n - столбцов, элементами которой являются действительные числа

Обратная матрица – матрица А^-1, при умножении которой на данную матрицу А справа или слева в результате получается единичная матрица Е

Минор элемента аij матрицы А n - го порядка – определитель (n-1) – го порядка, полученный путем вычеркивания i – ой строки и j – го столбца в матрице А

Ранг матрицы – наивысший порядок отличного от нуля минора матрицы

Коллинеарные векторы – векторы, лежащие на одной или параллельных прямых

Компланарные векторы – три вектора, лежащие на одной плоскости или на параллельных плоскостях

Векторное пространство – множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножение вектора на число, удовлетворяющее свойствам 1°-8°

Линейно-зависимые векторы – это такие векторы 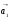, ,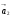…, 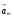векторного пространства, для которых существуют такие числа 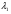, , 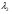…, , не равные одновременно нулю, что

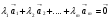
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов

Базис пространства – это совокупность n-линейно независимых векторов n-мерного пространства

Прямая на плоскости – геометрическое место точек, удовлетворяющих уравнению первой степени Ах +Ву + С = 0, где х, у – координаты текущей точки

Плоскость – геометрическое место точек, удовлетворяющих уравнению первой степени 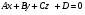, где x,y, z – координаты текущей точки

Скалярное произведение векторов 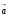и 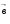- число, полученное в результате произведения длин этих векторов на косинус угла между ними

Функция – это соответствие, согласно которому каждому элементу х из некоторого множества Х отвечает вполне определенное число у из множества У

Элементарные функции – это функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции

Пределом функции у = f(х) при х, стремящемся к 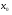, называется число А, если для любого числа Е>0 существует число 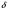>0 такое, что для всех х, удовлетворяющих неравенству 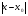< 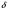выполняется неравенство |f(x) - A|<E

Первым замечательным пределом называется

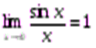
Вторым замечательным пределом называется предел числовой последовательности

Производная функции у = f(х) – это предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

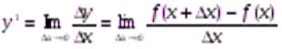
Точкой максимума функции y = f(x) называется такая точка х₀, что в некоторой окрестности точки х₀выполняется неравенство

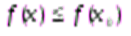
Точкой минимума функции y = f(x) называется такая точка х₀, что в некоторой окрестности точки х₀выполняется неравенство

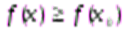
Критическая точка – это точка 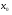, в которой производная равна нулю или не существует

Выпуклой вниз на промежутке Х называется такая функция y =f (x), что для любых двух значении 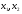Є Х из этого промежутка выполняется неравенство

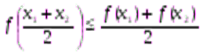
Выпуклой вверх на промежутке Х называется такая функция y =f (x), что для любых двух значении 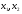Є Х из этого промежутка выполняется неравенство

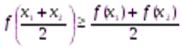
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх

Асимптота графика функции – это прямая, обладающая тем свойством, что расстояние от точки графика (х, f(х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат

Дифференциал функции – это главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной

dy=f''(x)*Dx

Первообразной функцией для функции y=f(x) на промежутке Х называется такая функция F(x), если в каждой точке х на промежутке Х выполняется условие

F'(x)=f(x)

Неопределенный интеграл от функции f(x) на промежутке Х – совокупность всех первообразных для функции f(x). Записывают:

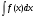=F(x)+C, где С – произвольная постоянная

Определенный интеграл от функции y=f(x) на [а, в] – это предел интегральной суммы 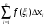при стремлении max 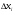к нулю. Записывают:

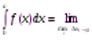
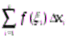
Функция нескольких переменных – это соответствие, при котором каждому набору значений ( 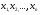) из некоторого множества Х соответствует одно вполне определенное значение переменной величины Z

Дифференциальные уравнения – это уравнения, связывающие искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции

Числовой ряд – это бесконечная последовательность чисел 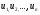,…, соединенных знаком сложения:

Сходящий ряд – это ряд, для которого существует конечный предел последовательности его частичных сумм, т.е.

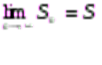
Степенный ряд – это ряд, членами которых являются функции

Ряд Маклорена – это ряд

---

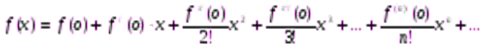
Дата добавления: 2019-09-13; просмотров: 224; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!