Последовательность преобразований при построении графиков.
Пусть задан график функции y = f(x) и нужно построить график функции y = m·f(kx + l) + n, где k, l, m, n - числа.
1. Записываем формулу функции в виде y = m·f(k·(x + l/k)), т.е. выносим за скобки коэффициент при х в аргументе функции.
2. Производим сжатие с коэффициентом k вдоль оси Ох к оси Oy. (Если k < 1, то получится растяжение от оси Oy.)
3. Если k < 0, то симметрично отображаем график относительно относительно оси Oy.
4. Осуществляем параллельный перенос (сдвиг) полученного графика на l/k единиц влево или вправо (в зависимости от знака, для положительного числа влево).
5. Производим растяжение с коэффициентом m от оси Oх (вдоль оси Оy). (Если m < 1, то получится сжатие к оси Ox.)
6. Если m < 0, то симметрично отображаем график относительно оси Ox.
7. Осуществляем параллельный перенос (сдвиг) полученного графика на n единиц вверх или вниз (в зависимости от знака, при n >0 вверх).
Лекция по теме «Производная»
Производная суммы равна сумме производных
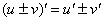
Пример 3
Найти производную функции 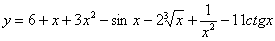
Пример 4
Найти производную функции 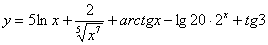
Производная произведения функций
Вроде бы по аналогии напрашивается формула 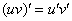 …., но неожиданность состоит в том, что:
…., но неожиданность состоит в том, что:
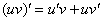
Пример 5
Найти производную функции 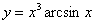
Пример 6
Найти производную функции 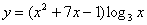
Пример 7
Найти производную функции 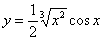
Производная частного функций
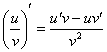
Пример 8
Найти производную функции 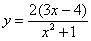
Пример 9
Найти производную функции 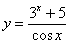
Пример 10
|
|
|
Найти производную функции 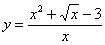
В данном случае можно почленно поделить числитель на знаменатель.
Преобразуем функцию:
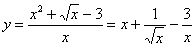
Пример 11
Найти производную функции 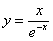
Здесь ситуация похожа, превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак:
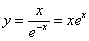
Произведение все-таки дифференцировать проще:
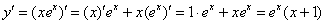
Пример 12
Найти производную функции 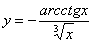
Производная сложной функции. Примеры решений
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
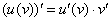
Функцию 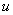 я буду называть внешней функцией, а функцию
я буду называть внешней функцией, а функцию 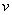 – внутренней (или вложенной) функцией.
– внутренней (или вложенной) функцией.
Пример 1
Найти производную функции 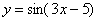
Пример 2
Найти производную функции 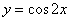
Пример 3
Найти производную функции 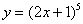
Пример 4
Найти производную функции 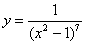
Пример 5
а) Найти производную функции 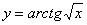
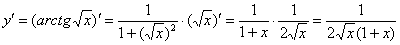
б) Найти производную функции 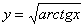
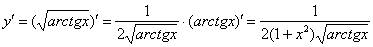
Пример 6
Найти производную функции 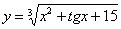
Пример 7
Найти производную функции 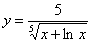
Пример 8
Найти производную функции 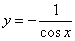
Здесь можно использовать правило дифференцирования частного 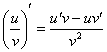 , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
, но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
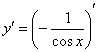
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
|
|
|
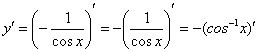
Пример 9
Найти производную функции 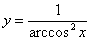
Пример 10
Найти производную функции 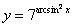
Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:

Пример 11
Найти производную функции 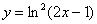
Пример 12
Найти производную функции 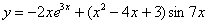
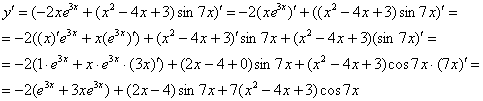
Пример 13
Найти производную функции 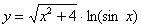
Вторая производная
Всё очень просто. Вторая производная – это производная от первой производной: 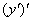
Стандартные обозначения второй производной: 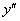 ,
, 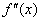 или
или 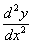
Аналогично можно найти вторую и третью производную.
Числовые ряды.
Определение 1: Числовым рядом называется
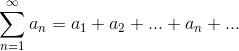 Например,
Например,
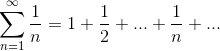 Определение 2: Числовой ряд
Определение 2: Числовой ряд 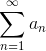 называется сходящимся, если последовательность частичных сумм этого ряда: называется сходящимся, если последовательность частичных сумм этого ряда:
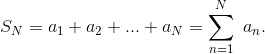 конечна.
Суммой числового ряда в этом случае называется предел конечна.
Суммой числового ряда в этом случае называется предел
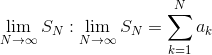 Если предел не существует либо бесконечен, то ряд расходится.
Пример. Исследуем на сходимость следующий ряд
Если предел не существует либо бесконечен, то ряд расходится.
Пример. Исследуем на сходимость следующий ряд 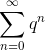
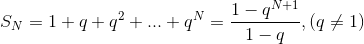 При
При 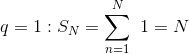 Если
Если  , то , то 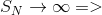 ряд расходится.
Если ряд расходится.
Если 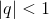 , то , то 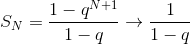 .
Ряд сходится и .
Ряд сходится и 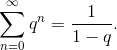 Если
Если 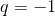 или или 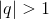 , то поскольку , то поскольку 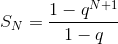 не имеет конечного предела, ряд расходится.
Итак, не имеет конечного предела, ряд расходится.
Итак, 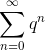 сходится при сходится при 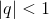 При остальных q ряд расходится.
Теорема 1: Необходимое условие сходимости ряда.
Если ряд
При остальных q ряд расходится.
Теорема 1: Необходимое условие сходимости ряда.
Если ряд 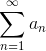 сходится, то сходится, то 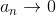 (при (при 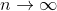 ).
Обратное утверждение неверно, у ряда ).
Обратное утверждение неверно, у ряда 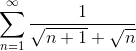 общий член общий член 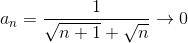 , но ряд расходится.
Простейшие свойства числовых рядов.
1. Линейность.
Если ряды , но ряд расходится.
Простейшие свойства числовых рядов.
1. Линейность.
Если ряды 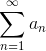 и и 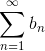 сходятся (и их суммы соответственно равны сходятся (и их суммы соответственно равны 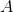 и и  ), то линейная комбинация ), то линейная комбинация 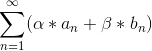 тоже сходится (к сумме тоже сходится (к сумме  ).
Это свойство вытекает из линейности предела:
2. На сходимость ряда не влияет изменение первых членов ряда: ).
Это свойство вытекает из линейности предела:
2. На сходимость ряда не влияет изменение первых членов ряда:
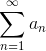 и и 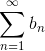 сходятся или расходятся одновременно, если сходятся или расходятся одновременно, если 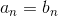 при при 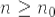 (конечно, суммы, в которые сходятся ряды разные).
Дело в том, что частичные суммы при (конечно, суммы, в которые сходятся ряды разные).
Дело в том, что частичные суммы при 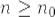 этих рядов отличаются на постоянную величину: этих рядов отличаются на постоянную величину: 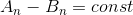 (при (при 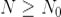 ). Следовательно, если ). Следовательно, если 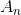 имеет предел, то и имеет предел, то и 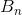 имеет его (и наоборот).
Знакоположительные числовые ряды.
Рассмотрим один из частных случаев числовых рядов так называемые знакоположительные числовые ряды. Для них верно следующее неравенство имеет его (и наоборот).
Знакоположительные числовые ряды.
Рассмотрим один из частных случаев числовых рядов так называемые знакоположительные числовые ряды. Для них верно следующее неравенство 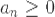 .
Теорема 2: Критерий сходимости знакоположительных рядов.
Ряд .
Теорема 2: Критерий сходимости знакоположительных рядов.
Ряд 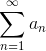 сходится сходится 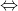 последовательность частичных сумм последовательность частичных сумм 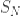 ограничена.
Теорема 3: Первый признак сравнения.
Пусть ограничена.
Теорема 3: Первый признак сравнения.
Пусть 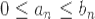 . Тогда:
1. Если . Тогда:
1. Если 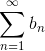 сходится, то сходится, то 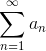 сходится.
2. Если сходится.
2. Если 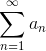 расходится, то расходится, то 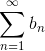 расходится.
Теорема 4: Второй признак сравнения.
Пусть расходится.
Теорема 4: Второй признак сравнения.
Пусть 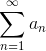 и и 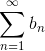 - знакоположительные ряды, причём - знакоположительные ряды, причём 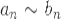 при при 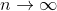 . Тогда эти два ряда сходятся или расходятся одновременно.
Теорема 5: Признак Даламбера.
Пусть . Тогда эти два ряда сходятся или расходятся одновременно.
Теорема 5: Признак Даламбера.
Пусть 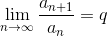 . Тогда:
1. Если . Тогда:
1. Если 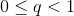 , то ряд сходится.
2. Если , то ряд сходится.
2. Если 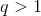 , то ряд расходится.
Теорема 6: Радикальный признак Коши.
Пусть , то ряд расходится.
Теорема 6: Радикальный признак Коши.
Пусть 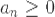 и существует предел и существует предел 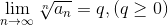 . Тогда:
1. Если . Тогда:
1. Если 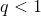 , то ряд сходится.
2. Если , то ряд сходится.
2. Если 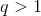 , то ряд расходится.
Теорема 7: Интегральный признак Коши.
Пусть , то ряд расходится.
Теорема 7: Интегральный признак Коши.
Пусть 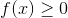 определена на определена на 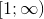 , непрерывна там и является невозрастающей. Тогда ряд , непрерывна там и является невозрастающей. Тогда ряд 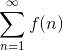 сходится сходится 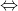 сходится интеграл сходится интеграл  .
Пример. Исследование ряда Дирихле .
Пример. Исследование ряда Дирихле  . .
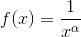 монотонно убывает, непрерывна. монотонно убывает, непрерывна.
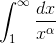 сходится при сходится при 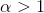 и расходится при и расходится при 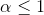 .
Следовательно: {tex}\sum_{n=1}^{\infty}\frac{1}{n^{\alpha }} сходится при .
Следовательно: {tex}\sum_{n=1}^{\infty}\frac{1}{n^{\alpha }} сходится при 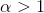 и расходится при и расходится при 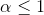 .
Оценить частичные сумма ряда можно следующим способом (следует из доказательства теоремы об интегральном признаке Коши): .
Оценить частичные сумма ряда можно следующим способом (следует из доказательства теоремы об интегральном признаке Коши):
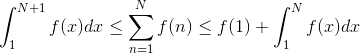 .
Знакопеременные и знакочередующиеся ряды.
Рассмотрим ещё два интересных частных случая числовых рядов - это знакопеременные и знакочередующиеся ряды.
Определение 3. Ряд называется знакочередующимся, если он имеет вид: .
Знакопеременные и знакочередующиеся ряды.
Рассмотрим ещё два интересных частных случая числовых рядов - это знакопеременные и знакочередующиеся ряды.
Определение 3. Ряд называется знакочередующимся, если он имеет вид:
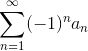 (или (или 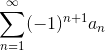 ), где ), где 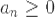 .
Ряды, не являющиеся знакопостоянными ( .
Ряды, не являющиеся знакопостоянными ( 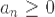 или или 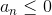 ) называются знакопеременными.
Например, ) называются знакопеременными.
Например, 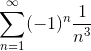 - знакочередующийся ряд, - знакочередующийся ряд, 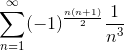 - знакопеременный ряд.
Признак Даламбера и оба признака Коши в случае знакопеременных и знакочередующихся рядов не работают!
Определение 4. Ряд - знакопеременный ряд.
Признак Даламбера и оба признака Коши в случае знакопеременных и знакочередующихся рядов не работают!
Определение 4. Ряд 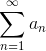 называется абсолютно сходящимся, если называется абсолютно сходящимся, если 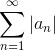 сходится.
Определение 5. Ряд называется условно сходящимся, если он сходится, но не является абсолютно сходящимся.
Теорема 8: Абсолютно сходящийся ряд сходится.
Теорема9: Признак Лейбница.
Пусть сходится.
Определение 5. Ряд называется условно сходящимся, если он сходится, но не является абсолютно сходящимся.
Теорема 8: Абсолютно сходящийся ряд сходится.
Теорема9: Признак Лейбница.
Пусть 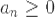 монотонно невозрастает и монотонно невозрастает и 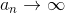 . Тогда ряд . Тогда ряд 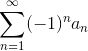 сходится.
Из этой статьи Вы узнали:
· числовые ряды: свойства числовых рядов, сходимость числовых рядов и необходимый признак сходимости числового ряда
· знакоположительные числовые ряды: признаки сходимости(интегральный , Коши, Даламбера, сравнения)
· знакопеременные и знакочередующиеся ряды: абсолютная сходимость и условная сходимость. признак Лейбница. сходится.
Из этой статьи Вы узнали:
· числовые ряды: свойства числовых рядов, сходимость числовых рядов и необходимый признак сходимости числового ряда
· знакоположительные числовые ряды: признаки сходимости(интегральный , Коши, Даламбера, сравнения)
· знакопеременные и знакочередующиеся ряды: абсолютная сходимость и условная сходимость. признак Лейбница.
|
|
|
|
|
|
|
Задача 1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 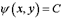 .)
.)
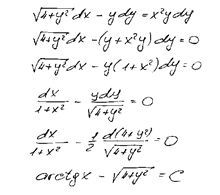
Задача 2. Найти общий интеграл дифференциального уравнения 
Задача 3. Найти общий интеграл дифференциального уравнения 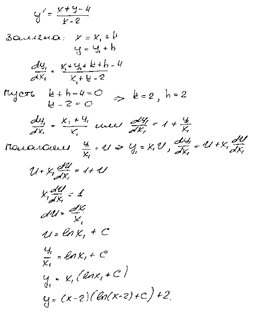 Задача 4.Найти решение задачи Коши
Задача 4.Найти решение задачи Коши

Задача 5. Найти решение задачи Коши 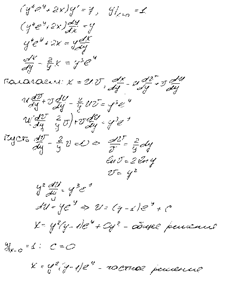
Задача 6. Найти решение задачи Коши 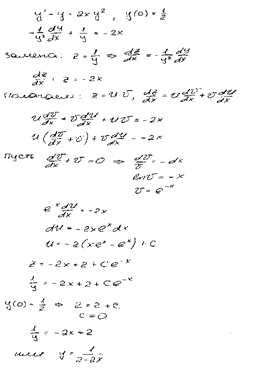
Задача 9. Найти линию, проходящую через точку 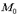 и обладающую тем свойством, что в любой ее точке
и обладающую тем свойством, что в любой ее точке 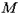 касательный вектор
касательный вектор 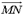 с концом на оси
с концом на оси 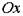 имеет проекцию на ось
имеет проекцию на ось 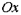 , обратно пропорциональную абсциссе точки
, обратно пропорциональную абсциссе точки 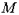 . Коэффициент пропорциональности равен
. Коэффициент пропорциональности равен 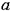

Задача 10. Найти общее решение диф. уравнения. 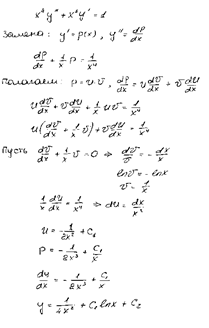
Задача 11. Найти решение 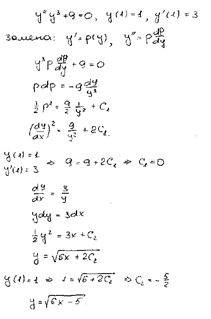
Задача 12Найти общее решение дифференциального уравнения. 
Задача 13Найти общее решение 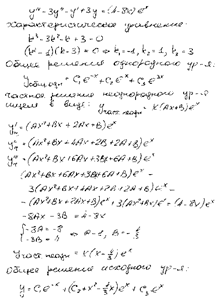
Задача 14 Найти общее решение дифференциального уравнения. 
Задача15. Найти общее решение диф. 
Задача 16. Найти решение задачи Коши  Задача 7. Найти общий интеграл Дифференциального уравнения
Задача 7. Найти общий интеграл Дифференциального уравнения  .
.
Практический раздел
ТЕМЫ СЕМИНАРСКИХ ЗАНЯТИЙ
| Название темы | Содержание |
| 1.1. Векторная алгебра | Векторы. Алгебраические операции над векторами и их свойства. Линейно зависимые векторы. Скалярное произведение векторов. |
| 1.2.Аналитическая геометрия на плоскости | Уравнение прямой в векторной форме; различные уравнения прямой. Взаимное расположение прямых. Расстояние от точки до прямой. Угол между прямыми |
| Кривые второго порядка: окружность, эллипс, гипербола, парабола. | |
| 1.3. Элементы аналитической геометрии в пространстве | Простейшие задачи аналитической геометрии в пространстве. Основные виды уравнений плоскости и прямой в пространстве. Угол между плоскостями, между прямыми, между прямой и плоскостью. Расстояние от точки до плоскости. |
| 1.4. Матицы | Основные арифметические операции над матрицами и их свойства. Матричный метод и его применение в экономических исследованиях. |
| Вычисление определителей. Вычисление обратной матрицы. Определение ранга матрицы. Элементарные преобразования матриц. Собственные числа и собственные векторы матрицы. | |
| 1.5. Системы линейных уравнений и неравенств | Элементарные преобразования системы. Метод Гаусса. Базисные и свободные неизвестные. Правило Крамера. |
| Межотраслевой баланс производства и выпуска продукции. Однородные системы линейных уравнений. Графический метод решения системы линейных неравенств с двумя переменными. | |
| 2.1. Числовая последовательность и ее предел | Вычисление пределов последовательностей. Бесконечно малые и бесконечно большие последовательности |
| 2.2. Предел функции одной переменной | Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций.
Раскрытие неопределенностей 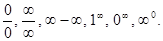
|
| 2.3. Непрерывные функции одной переменной | Непрерывность функции в точке. Арифметические операции над непрерывными функциями. Точки разрыва и их классификация. Непрерывность сложной и обратной функций. Непрерывность элементарных функций. |
| 2.4. Производная и дифференциал функции одной переменной | Определение производной функции в точке. Односторонние производные. Геометрический, механический и экономический смысл производной. Непрерывность функции, имеющей производную. Правила дифференцирования. Производная сложной и обратной функций. Производные основных элементарных функций. Логарифмическая производная. |
| Дифференциал функции одной переменной. Инвариантность формы записи первого дифференциала. Применение дифференциала в приближенных вычислениях. Производные высших порядков. Неявные функции. Дифференциалы высших порядков. | |
| 2.6. Приложения дифференциального исчисления | Условия постоянства функции. Критерий монотонности. Экстремум функции. Необходимое и достаточные условия экстремума. |
| Выпуклость вверх и вниз. Точки перегиба. Асимптоты графика функции. функций Построение графиков функций. Наименьшее и наибольшее значение функции на отрезке. Решение задач с экономическим содержанием | |
| 2.7.Функции нескольких переменныъх | Производственные функции. Линии изоквант и изокост. Предел функции двух переменных. Частные производные первого и высшего порядков. Производная по направлению. Градиент функции и его свойства. |
| Необходимые и достаточные условия экстремума функции двух переменных. Условный экстремум. Наибольшее и наименьшее значения функции двух переменных в замкнутой области. Оценка параметров функций, используемых в экономических исследованиях, при помощи метода наименьших квадратов. | |
| 2.8. Первообразная и неопределенный интеграл | Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Неопределённый интеграл с логарифмической производной. |
| Интегрирование при помощи подстановки. Интегрирование по частям. Интегрирование простейших рациональных дробей; рациональных функций; иррациональных функций; выражений, содержащих тригонометрические функции. | |
| Определенный интеграл | Формула Ньютона-Лейбница. Вычисление определенного интеграла заменой переменной. Вычисление определенного интеграла по частям. Приближенное вычисление определенных интегралов: формулы прямоугольников, трапеций, Симпсона |
| Геометрические приложения определенных интегралов: вычисление площадей плоских фигур, объемов тел вращения. Применение определенного интеграла в экономических исследованиях Несобственные интегралы. Несобственные интегралы по бесконечному промежутку.Несобственные интегралы от неограниченных функций. Их сходимость. | |
| 2.10. Кратные интегралы | Определение двойного интеграла. Геометрический смысл двойного интеграла. Сведение двойного интеграла к повторному. Тройной интеграл. Приложения кратных интегралов |
| 2.11. Обыкновенные дифференциальные уравнения | Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными и их применение в экономических исследованиях Линейные дифференциальные уравнения первого порядка и их применение в экономических исследованиях. Однородные дифференциальные уравнения первого порядка и их применение в экономических исследованиях. |
| Линейные однородные дифференциальные уравнения второго порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения второго порядка.. | |
| Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами со специальной правой частью. Метод Лагранжа вариации произвольной постоянной. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. | |
| 2.12. Ряды | Свойства сходящихся рядов. Необходимый признак сходимости. Достаточные признаки сходимости числовых знакоположительных рядов: признаки сравнения; признаки Даламбери и Коши; интегральный признак. Знакочередующиеся числовые ряды. Признак Лейбница. Оценка остатка знакочередующегося ряда. |
| Разложение основных элементарных функций ех , cos x, sin x, (1+x)m , ln (1+x) в ряд Маклорена. Применение степенных рядов в приближенных вычислениях. | |
| Ряды Фурье. Разложение функций в ряды Фурье. | |
| 3.1. Основные понятия и теоремы теории вероятностей | Пространство элементарных событий. Соотношения между событиями. Вероятность. Методы вычисления вероятностей |
| Свойства вероятностей. Теорема сложения. Условная вероятность и ее свойства. Независимость событий. Теорема умножения. | |
| Формула полной вероятности и формулы Байеса. Байесовский анализ возможных решений в экономике. | |
| 3.2. Повторные независимые испытания | Последовательность независимых повторных испытаний. Формула Бернулли. Наивероятнейшее число успехов в формуле Бернулли. Теорема Пуассона. Локальная и интегральная формулы Муавра-Лапласа. |
| 3.3. Случайные величины. Основные законы распределения случайных величин | Функция распределения и ее свойства. Дискретные случайные величины. Закон распределения дискретной случайной величины. |
| Непрерывные случайные величины. Числовые характеристики случайных величин. Математическое ожидание и его свойства. Мода и медиана. Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение. Моменты распределения случайных величин. Асимметрия и эксцесс. | |
| Важнейшие распределения дискретных случайных величин. Биномиальное распределение. Распределение Пуассона. Геометрическое и гипергеометрическое распределения. Важнейшие распределения непрерывных случайных величин. Равномерное распределение. Нормальное распределение. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный интервал. Показательное распределение. | |
| Зависимые и независимые случайные величины. Корреляционный момент и коэффициент корреляции. | |
| 3.4. Закон больших чисел | Неравенства Маркова, Чебышева, Колмогорова. Теоремы Чебышева, Хинчина, Маркова и Бернулли. Центральная предельная теорема в формулировке Линдеберга-Леви, Ляпунова. Нормальное распределение как предельное для биномиального и пуассоновского распределения. |
| 3.5. Основы математической статистики | Статистические распределения. Графическое представление распределений. Эмпирическая функция распределения. Основные числовые характеристики выборки: среднее арифметическое, мода, медиана, стандартная ошибка, вариационный размах, среднее линейное отклонение, коэффициенты вариации, начальные и центральные моменты, асимметрия, эксцесс. |
| Точечное оценивание. Свойства точечных оценок. Оценки математического ожидания, дисперсии. Интервальное оценивание. Доверительный интервал и доверительная вероятность. Методы построения доверительных интервалов. | |
| Определение статистической гипотезы, критерия, ошибок первого и второго рода; определение критической области, мощности критерия; схема проверки статистической гипотезы. Проверка гипотез о математическом ожидании и дисперсии случайной величины, распределенной по нормальному закону. Проверка гипотез о равенстве математических ожиданий и дисперсий. Критерии согласия Пирсона, Романовского, Колмогорова. | |
| Однофакторный и двухфакторный дисперсионный анализ. Линейная корреляционная зависимость и линии регрессии. Проверка значимости уравнения и коэффициентов уравнения регрессии. Ранговая корреляция. | |
| 4.1. Линейное программирование | Геометрическая интерпретация задачи линейного программирования. Графический метод решения. задач линейного программирования. Опорные планы задачи линейного программирования. |
| Симплексный метод решения задач линейного программирования. | |
| Двойственность в линейном программировании Транспортная задача. Метод потенциалов для решения транспортной задачи. Применение пакета прикладных программ QSBR и Excel для решения задач линейного программирования. | |
| 4.2. Целочисленное программирование | Задачи целочисленного программирования: общая задача о расписании, задача коммивояжера, задача о разбиении, покрытии и упаковке, задача о размещении оборудования, задача раскроя. |
| Методы ветвей и границ. Методы отсечений. | |
| 4.3. Нелинейное программирование | Постановка задачи нелинейного программирования и ее геометрическая интерпретация. Метод множителей Лагранжа. Выпуклое программирование. Задачи выпуклого программирования. Выпуклые и вогнутые функции. Теорема Куна-Таккера. Понятие о глобальном и о локальном оптимуме. Квадратичное программирование. |
| Приближенные методы решения задач нелинейного программирования с сепарабельными функциями. | |
| 4.4. Динамическое программирование | Примеры задач, решаемых методом динамического программирования. Вычислительная схема метода динамического программирования. |
| Динамические задачи выбора наиболее экономичного маршрута доставки груза, оптимального распределения средств на расширение производства, определения оптимальной стратегии замены оборудования, формирования оптимальной программы производства с учетом запасов (в зависимости от специальности). |
СПИСОК ЛИТЕРАТУРЫ
Основная литература
2. Гусак А.А. Высшая математика. Том 1, 2. – Мн.: ТетраСистемс, 2001г.
3. Булдык Г.М. Курс лекций по высшей математике. – Мн.: ФУАинформ, 2009 г.
4. Булдык Г.М. Сборник задач и упражнений по высшей математике. – Мн.: ФУАинформ, 2009 г.
5. Булдык Г.М. Высшая математика. Задания для самостоятельной работы студентов всех специальностей (РГР № 1).
6. Булдык Г.М. Высшая математика. Задания для самостоятельной работы студентов всех специальностей (РГР № 2).
7. Чумаков Ф.В. Высшая математика: в 3 ч.Ч. 1. Линейная алгебра и аналитическая геометрия: учеб. пособие. – Мн.: Тесей, 2008 г.
8. Чумаков Ф.В., Василец С.И. Интегрирование: учебно-методическое пособие – Мн.: БГПУ, 2008г.
9. Булдык Г.М. Теория вероятностей и математическая статистика. Мн.: Выш. школа, 1989г.
10. Боровков А.А. Курс теории вероятностей. – М.: Наука, 1972г.
11. Булдык Г.М. Высшая математика. Теория вероятностей и математическая статистика. События и вероятности. \ Уч. пособие. – Мн., ИПД, 2005г.
12. Булдык Г.М. Руководство к решению задач и упражнений по теории вероятностей и математической статистике. – Мн.: ФУАинформ, 2009 г.
13. Булдык Г.М., Серебрякова Н.Г. Теория вероятностей. Случайные величины. Системы случайных величин. \ Уч. пособие. – Мн., ИПД, 2006г.
14. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001г.
15. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1999г.
16. Гусак А.А., Бричикова Е.А. Теория вероятностей. Справочное пособие к решению задач. – Мн.: ТетраСистемс, 2002г.
17. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию. Мн.: Выш. шк., 2001г.
18. Кузнецов А.В., Новикова Г.И., Холод Н.И. Сборник задач по математическому программированию. Мн.: Вышэйшая школа, 2003г.
19. Кузнецов А.В.,Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. Мн.: Выш. шк., 1994г.
Дополнительная литература
1. Кремер Н.Ш. и др. Высшая математика для экономистов – М., 1997 г
2. Кузнецов А.В., Кузнецова Д.С. и др. Сборник задач и упражнений по высшей математике: Общий курс. – Мн.: Выш.школа, 1994г.
3. Гусак А.А. Задачи и упражнения по высшей математике. Мн.: Вышэйшая школа, 1988г.
4. Кудрявцев Л.Д. Курс математического анализа. В 2 т. М.: Высшая школа, 1969г.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1.
1.
Пять занумерованных шаров расставляются в случайном порядке. Рассматриваются события A={шарик с номером 1 оказался третьим слева} и B={шарик с номером 2 оказался левее шарика с номером 1}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [0, 1], и независимо от нее точка с координатой h выбирается наудачу на отрезке [0, 2]. Проверить, являются ли три события {x+h < 1}, {x > h} и {h = 1} независимыми в совокупности.
3.
Четырнадцать раз подбрасывается пара игральных костей. Какова вероятность того, что сумма очков, равная 4, выпадет не менее пяти раз?
4.
В первой урне 7 белых и 2 черных шара, во второй - 4 белых и 5 черных. Из первой урны наудачу выбирают три шара и перекладывают во вторую, после чего из второй урны берут один шар. Найти вероятность того, что этот последний шар окажется белым.
5.
Один стрелок попадает по мишени с вероятностью 0.4, другой — с вероятностью 0.7 независимо от первого. Стрелки делают по одному выстрелу. С какой вероятностью хотя бы один из них попадет по мишени?
6.
Игральную кость подбрасывают до первого выпадения шестерки. Найти вероятность того, что при этом ни разу не выпадет единица.
1.
Четыре занумерованных шара раскладываются в три ящика (красный, синий и зеленый) так, что для каждого шара равновозможно попасть в любой ящик. Рассматриваются события A={шарик с номером 1 попал в синий ящик} и B={шарики с номерами 1 и 2 оказались в разных ящиках}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [0, 2], и независимо от нее точка с координатой h выбирается наудачу на отрезке [0, 3]. Проверить, являются ли три события {x+h < 2}, {h = 1} и {x > h} независимыми в совокупности.
3.
Семь раз подбрасываются три игральные кости. Какова вероятность того, что сумма очков, равная 17, выпадет не более трех раз?
4.
В первой урне 8 белых и 3 черных шара, во второй - 5 белых и 3 черных. Из первой урны наудачу выбирают два шара, а из второй — один шар. После этого из выбранных трех шаров наудачу берут один шар. Найти вероятность того, что этот последний шар окажется белым.
5.
Первая лампочка перегорает с вероятностью 2/3, вторая — с вероятностью 3/5 независимо от первой. С какой вероятностью перегорит хотя бы одна лампочка?
6.
На 10 полях лотерейного билета скрыто слово «автомобиль», остальные 10 полей пусты. Игрок может открыть от 10 до 13 полей. Найти вероятность того, что игроку удалось вскрыть слово «автомобиль», но для этого ему понадобилось открыть 13 полей.
1.
Подбрасываются три игральные кости. Рассматриваются события A={на третьей кости выпало 3 очка} и B={на второй кости выпало меньше очков, чем на третьей}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [0, 1], и независимо от нее точка с координатой h выбирается наудачу на отрезке [-1, 1]. Проверить, являются ли три события {h = 0}, {x < h} и {x+h < 1} независимыми в совокупности.
3.
Девять раз подбрасывается пара игральных костей. Какова вероятность того, что сумма очков, равная 10, выпадет не менее двух раз?
4.
В первой урне 2 белых и 5 черных шаров, во второй — 7 белых и 5 черных. Из первой урны наудачу выбирают три шара и перекладывают во вторую, после чего из второй урны берут один шар. Найти вероятность того, что этот последний шар окажется черным.
5.
Устройство содержит два независимо работающих элемента. Первый отказывает с вероятностью 0.7, второй — с вероятностью 0.5. С какой вероятностью откажет хотя бы один из этих двух элементов?
6.
Из полной колоды вынимается одна карта, которая затем возвращается обратно в колоду. Эксперимент прекращается при первом появлении пиковой карты. Найти вероятность того, что при этом ни разу не будет вынута бубновая карта.
1.
Из полной колоды в 52 карты Вася, Петя и Коля выбирают по очереди наугад по одной карте. Рассматриваются события A={у Пети — дама пик} и B={у Васи — пиковая карта достоинством выше, чем у карты Пети}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [-1, 1], и независимо от нее точка с координатой h выбирается наудачу на отрезке [0, 2]. Проверить, являются ли три события {x+h < 0}, {x = 0} и {x+1 > h} независимыми в совокупности.
3.
Пять раз подбрасываются три игральные кости. Какова вероятность того, что сумма очков, равная 4, выпадет не более четырех раз?
4.
В первой урне 8 белых и 3 черных шара, во второй — 5 белых и 3 черных. Из первой урны наудачу выбирают один шар, а из второй — два шара. После этого из выбранных трех шаров наудачу берут один шар. Найти вероятность того, что этот последний шар окажется черным.
5.
Два орудия делают по одному выстрелу. Вероятность попадания в цель для первого орудия равна 3/4, для второго — 5/6 независимо от первого. С какой вероятностью произойдет хотя бы одно попадание?
6.
На 10 полях лотерейного билета скрыто слово «автомобиль», остальные 10 полей пусты. Игрок может открыть от 10 до 13 полей. Найти вероятность того, что игроку удалось вскрыть слово «автомобиль», но для этого ему понадобилось открыть 12 полей.
1.
Шесть томов энциклопедии расставляются на полке в случайном порядке. Рассматриваются события A={том номер 3 окажется предпоследним} и B={том номер 1 окажется правее тома номер 3}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [0, 2], и независимо от нее точка с координатой h выбирается наудачу на отрезке [0, 1]. Проверить, являются ли три события {x-1 > h}, {x+h < 2} и {x = 1} независимыми в совокупности.
3.
Двенадцать раз подбрасывается пара игральных костей. Какова вероятность того, что сумма очков, равная 11, выпадет не менее десяти раз?
4.
В первой урне 3 белых и 5 черных шаров, во второй — 5 белых и 6 черных. Из первой урны наудачу выбирают три шара и перекладывают во вторую, после чего из второй урны берут один шар. Найти вероятность того, что этот последний шар окажется белым.
5.
При обжиге тонкостенных деталей в одной печи доброкачественная продукция получается с вероятностью 0.9, в другой печи — с вероятностью 0.8 независимо от первой. С какой вероятностью из двух вышедших из обжига в разных печах деталей хотя бы одна будет доброкачественной?
6.
На отрезок [0,1] наудачу и независимо друг от друга бросаются 6 точек с координатами x1,...,x6. Доказать, что события {min(x1,...,x6) > 1/2} и {max(x1,...,x6) < 3/4} зависимы.
1.
В сплошном тумане для каждой из трех биатлонисток (L. Poire, U. Disl, O. Пылёва) равновозможно сделать от одного до пяти промахов. Рассматриваются события A={L. Poire промахнулась трижды} и B={О. Пылёва сделала меньше промахов, чем L. Poire}.
а) Описать пространство W элементарных исходов, найти число элементов в множестве W и вероятность P(AЗB);
б) привести примеры трех различных элементарных исходов w1, w2 и w3, благоприятствующих событиям A, B и AЗB соответственно.
2.
Точка с координатой x выбирается наудачу на отрезке [0, 3], и независимо от нее точка с координатой h выбирается наудачу на отрезке [0, 2]. Проверить, являются ли три события {x < h}, {x = 1} и {x+h < 2} независимыми в совокупности.
3.
Восемь раз подбрасываются три игральные кости. Какова вероятность того, что сумма очков, равная 17, выпадет не менее пяти раз?
4.
В первой урне 4 белых и 4 черных шара, во второй — 2 белых и 3 черных. Из первой урны наудачу выбирают два шара, а из второй — один шар. После этого из выбранных трех шаров наудачу берут один шар. Найти вероятность того, что этот последний шар окажется белым.
5.
Два стеклянных шарика бросают с 9 этажа. Первый разбивается с вероятностью 5/6, второй — с вероятностью 7/8. С какой вероятностью хотя бы один шарик из этих двух разобьется?
6.
Колода карт (52 карты) раздается поровну четырем игрокам — по 13 карт каждому. Найти вероятность того, что хотя бы у одного из игроков соберутся все карты одной масти.
2.
Найдите следующие пределы:
1.
а) 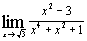 ; ;
| б) 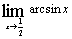 ; ;
| в) 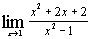 ; ;
|
г) 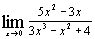 ; ;
| д) 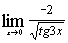 ; ;
| е) 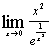 ; ;
|
ж) 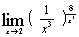 ; ;
| з) 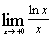 ; ;
| и) 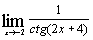 . .
|
2.
а) 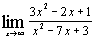 ; ;
| б) 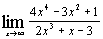 ; ;
|
в) 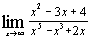 ; ;
| г) 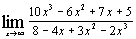 ; ;
|
д) 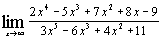 ; ;
| е) 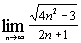 ; ;
|
ж) 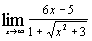 ; ;
| з) 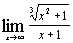 ; ;
|
и) 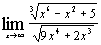 ; ;
| к) 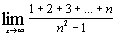 ; ;
|
л) 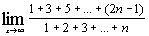 ; ;
| м) 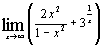 . .
|
3.
а) 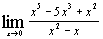 ; ;
| б) 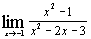 ; ;
|
в) 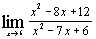 ; ;
| г) 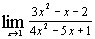 ; ;
|
д) 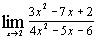 ; ;
| е) 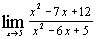 ; ;
|
ж) 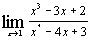 ; ;
| з) 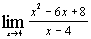 ; ;
|
и) 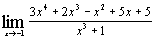 ; ;
| к) 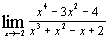 ; ;
|
л) 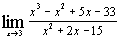 . .
|
4.
а) 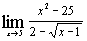 ; ;
| б) 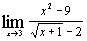 ; ;
|
в) 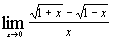 ; ;
| г) 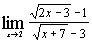 ; ;
|
д) 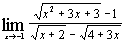 ; ;
| е) 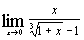 ; ;
|
ж) 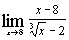 ; ;
| з) 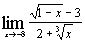 ; ;
|
и) 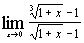 ; ;
| к) 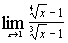 . .
|
5.
а) 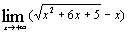 ; ;
| б) 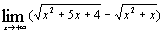 ; ;
|
в) 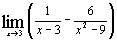 ; ;
| г) 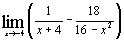 . .
|
6.
а) 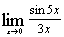 ; ;
| б) 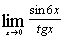 ; ;
|
в) 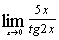 ; ;
| г) 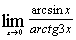 ; ;
|
д) 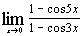 ; ;
| е) 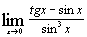 ; ;
|
ж) 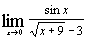 ; ;
| з) 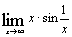 ; ;
|
и) 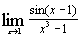 ; ;
| к) 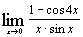 ; ;
|
л) 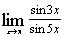 ; ;
| м) 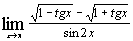 ; ;
|
н) 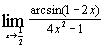 ; ;
| о) 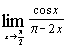 ; ;
|
п) 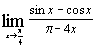 . .
|
7.
а) 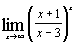 ; ;
| б) 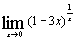 ; ;
|
в) 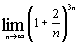 ; ;
| г) 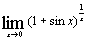 ; ;
|
д) 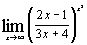 ; ;
| е) 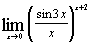 ; ;
|
ж) 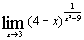 ; ;
| з) 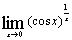 ; ;
|
и) 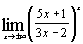 ; ;
| к) 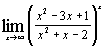 . .
|
8.
а) 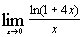 ; ;
| б) 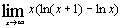 ; ;
|
в) 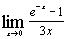 ; ;
| г) 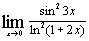 ; ;
|
д) 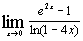 ; ;
| е) 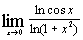 ; ;
|
ж) 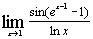 . .
|
Ответы. 1. а) 0; б) 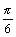 ; в)
; в) 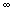 ; г) 0; д)
; г) 0; д) 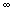 ; е) 0; ж)
; е) 0; ж) 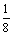 ; з)
; з) 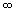 ; и) 0. 2. а) 3; б)
; и) 0. 2. а) 3; б) 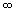 ; в) 0; г) –5; д) 0; е) 1; ж) 6; з) 0; и)
; в) 0; г) –5; д) 0; е) 1; ж) 6; з) 0; и) 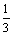 ; к)
; к) 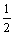 ; л) 2; м) –1.3. а) 0; б)
; л) 2; м) –1.3. а) 0; б) 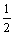 ; в)
; в) 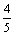 ; г)
; г) 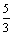 ; д)
; д) 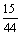 ; е)
; е) 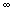 ; ж)
; ж) 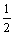 ; з) 2; и)
; з) 2; и) 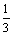 ; к) –
; к) –  ; л)
; л) 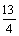 .4. а) –40; б) 24; в) 1; г) 6; д) –
.4. а) –40; б) 24; в) 1; г) 6; д) – 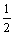 ; е) 3; ж) 12; з) –2; и)
; е) 3; ж) 12; з) –2; и) 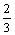 ; к)
; к) 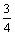 . 5. а) 3; б) 2; в)
. 5. а) 3; б) 2; в) 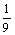 ; г) –
; г) – 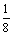 .6. а)
.6. а) 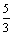 ; б) 6; в)
; б) 6; в) 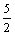 ; г)
; г) 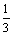 ; д)
; д) 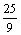 ; е)
; е) 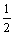 ; ж) 6; з) 1; и)
; ж) 6; з) 1; и) 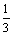 ; к) 8; л)
; к) 8; л) 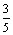 ; м) –
; м) – 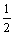 ; н) –
; н) – 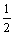 ; о)
; о) 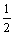 ; п) –
; п) – 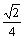 .7. а) е
.7. а) е 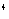 ; б) е
; б) е 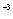 ; в) е
; в) е 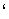 ; г) е; д) 0; е) 9; ж) е
; г) е; д) 0; е) 9; ж) е 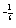 ; з) 1; и) +
; з) 1; и) + 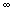 ;0; к) е
;0; к) е 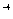 .8. а) 4; б) 1; в) –
.8. а) 4; б) 1; в) – 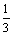 ; г)
; г) 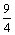 д) –
д) – 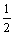 ; е) –
; е) – 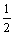 ; ж) 1.
; ж) 1.
3.
Найдите неопределенные интегралы, применяя основные правила интегрирования:
1. 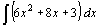 . .
| 2. 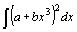 . .
| |
3. 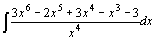 . .
| 4. 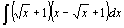 . .
| |
5. 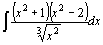 . .
| 6. | |
7. 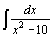 . .
| 8. | |
9. 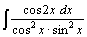 . .
| 10. | |
11. 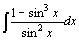 . .
| 12. | |
13. 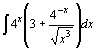 . .
| 14. | |
Найдите неопределенные интегралы, используя свойство дифференциала 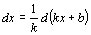 :
:
15. 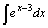 . .
| 16. 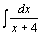 . .
| 17. 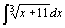 . .
|
18. 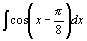 . .
| 19. 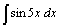 . .
| 20. 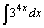 . .
|
21. 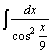 . .
| 22. 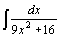 . .
| 23. 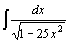 . .
|
24. 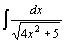 . .
| 25. 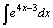 . .
| 26. 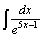 . .
|
27. 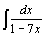 . .
| 28. 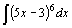 . .
| 29. 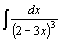 . .
|
30. 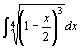 . .
| 31. 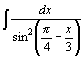 . .
| 32. 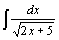 . .
|
Найдите неопределенные интегралы, используя подведение под знак дифференциала:
33. 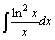 . .
| 34. 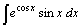 . .
| 35. 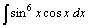 . .
|
36. 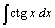 . .
| 37. 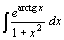 . .
| 38. 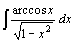 . .
|
39. 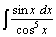 . .
| 40. 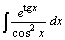 . .
| 41. 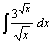 . .
|
42. 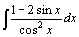 . .
| 43. 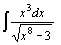 . .
| 44. 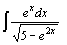 . .
|
45. 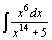 . .
| 46. 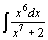 . .
| 47. 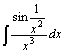 . .
|
48. 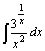 . .
| 49. 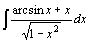 . .
| 50. 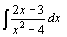 . .
|
51. 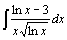 . .
| 52. 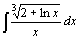 . .
| 53. 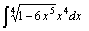 . .
|
54. 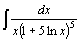 . .
| 55. 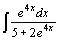 . .
| 56. 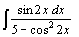 . .
|
Найдите неопределенные интегралы, используя метод интегрирования по частям:
57. 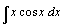 . .
| 58. 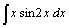 . .
| 59. 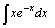 . .
|
60. 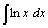
| 61. 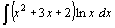 . .
| 62. 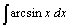 . .
|
63.  . .
| 64. 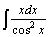 . .
| 65. 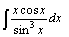 . .
|
66. 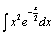 . .
| 67. 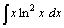 . .
| 68.  . .
|
Найдите неопределенные интегралы от рациональных дробей:
69. 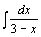 . .
| 70. 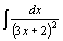 . .
| 71. 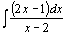 . .
|
72. 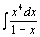 . .
| 73. 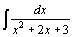 . .
| 74. 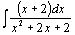 . .
|
75. 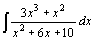 . .
| 76. 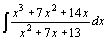 . .
| 77. 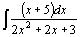 . .
|
78. 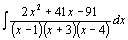 . .
| 79. 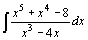 . .
| 80. 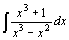 . .
|
81. 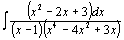 . .
| 82. 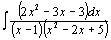 . .
| 83. 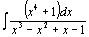 . .
|
Найдите неопределенные интегралы от иррациональных функций:
84. 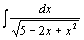 . .
| 85. 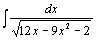 . .
| 86. 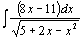 . .
|
87. 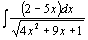 . .
| 88. 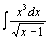 . .
| 89. 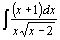 . .
|
90. 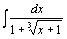 . .
| 91. 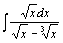 . .
| 92. 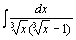 . .
|
93. 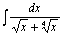 . .
| 94. 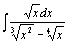 . .
| 95. 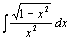 . .
|
96. 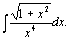
| 97. 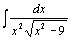 . .
| 98. 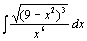 . .
|
Найдите неопределённые интегралы от тригонометрических функций:
99. 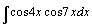 . .
| 100. 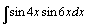 . .
| 101. 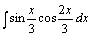 . .
|
102. 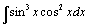 . .
| 103. 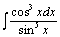 . .
| 104. 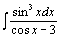 . .
|
105. 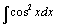 . .
| 106. 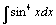 . .
| 107. 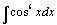 . .
|
108. 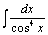 . .
| 109. 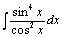 . .
| 110. 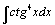 . .
|
111. 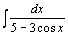 . .
| 112. 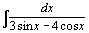 . .
| 113. 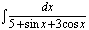 . .
|
Ответы. 1. 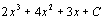 . 2.
. 2. 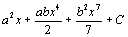 . 3.
. 3. 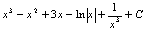 . 4.
. 4. 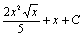 . 5.
. 5. 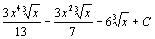 . 6.
. 6. 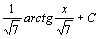 . 7.
. 7. 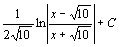 . 8.
. 8. 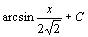 . 9.
. 9. 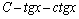 . 10.
. 10. 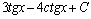 . 11.
. 11. 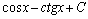 . 12.
. 12. 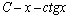 . 13.
. 13. 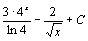 . 14.
. 14. 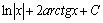 . 15.
. 15. 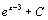 . 16.
. 16. 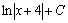 . 17.
. 17. 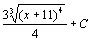 . 18.
. 18. 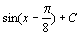 . 19.
. 19. 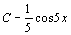 . 20.
. 20. 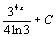 . 21.
. 21. 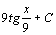 . 22.
. 22. 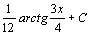 . 23.
. 23. 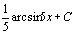 . 24.
. 24. 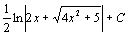 . 25.
. 25. 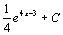 . 26.
. 26. 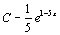 . 27.
. 27. 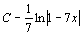 . 28.
. 28. 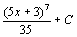 . 29.
. 29. 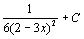 . 30.
. 30. 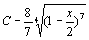 . 31.
. 31. 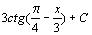 . 32.
. 32. 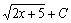 . 33.
. 33. 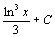 . 34.
. 34. 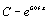 . 35.
. 35. 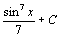 . 36.
. 36. 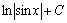 . 37.
. 37. 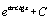 . 38.
. 38. 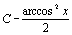 . 39.
. 39. 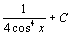 . 40.
. 40. 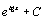 . 41.
. 41. 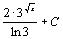 . 42.
. 42. 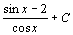 . 43.
. 43. 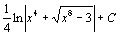 . 44.
. 44. 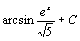 . 45.
. 45. 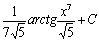 . 46.
. 46. 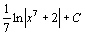 . 47.
. 47. 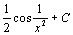 . 48.
. 48. 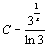 . 49.
. 49. 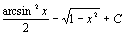 . 50.
. 50. 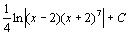 . 51.
. 51. 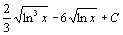 . 52.
. 52. 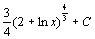 . 53.
. 53. 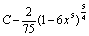 . 54.
. 54. 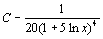 . 55.
. 55. 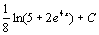 . 56.
. 56. 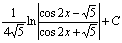 .57.
.57. 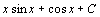 . 58.
. 58. 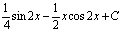 . 59.
. 59. 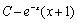 . 60.
. 60. 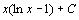 . 61.
. 61. 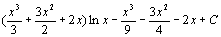 . 62.
. 62. 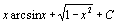 . 63.
. 63. 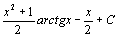 . 64.
. 64. 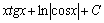 . 65.
. 65. 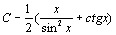 . 66.
. 66. 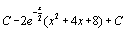 . 67.
. 67. 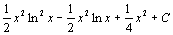 . 68.
. 68. 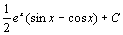 . 69.
. 69. 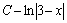 . 70.
. 70. 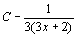 . 71.
. 71. 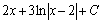 .72.
.72. 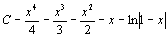 . 73.
. 73. 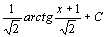 74.
74. 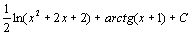 . 75.
. 75. 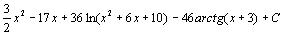 . 76.
. 76. 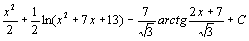 77.
77. 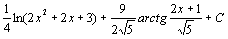 . 78.
. 78. 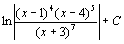 . 79.
. 79. 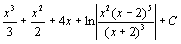 . 80.
. 80. 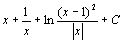 . 81.
. 81. 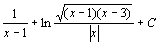 . 82.
. 82. 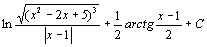 . 83.
. 83. 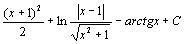 . 84.
. 84. 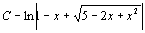 . 85.
. 85. 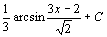 . 86.
. 86. 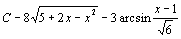 . 87.
. 87. 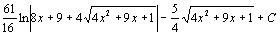 . 88.
. 88. 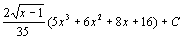 . 89.
. 89. 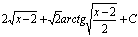 . 90.
. 90. 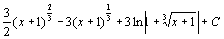 . 91.
. 91. 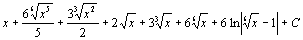 . 92.
. 92. 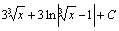 . 93.
. 93. 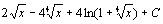 . 94.
. 94. 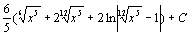 . 95.
. 95. 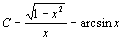 . 96.
. 96. 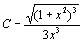 . 97.
. 97. 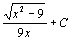 . 98.
. 98. 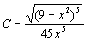 . 99.
. 99. 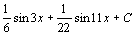 . 100.
. 100. 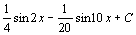 . 101.
. 101. 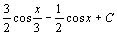 . 102.
. 102. 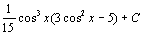 . 103.
. 103. 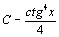 . 104.
. 104. 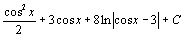 . 105.
. 105. 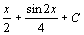 . 106.
. 106. 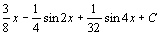 107.
107. 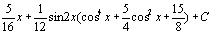 . 108.
. 108. 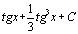 . 109.
. 109. 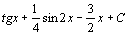 . 110.
. 110. 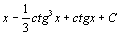 . 111.
. 111. 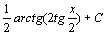 . 112.
. 112. 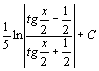 . 113.
. 113. 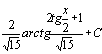 .
.
4.
1. Слово КОРОБОК составлено из букв разрезной азбуки Карточки с буквами тщательно перемешены. Пять карточек извлекается по очереди и раскладываются в ряд Какова вероятность получить таким путем слово КОРОК?
2. Первый станок выпускает бракованные детали с вероятностью 0,2, второй станок — с вероятностью 0,2. На первом станке изготовлены четыре детали, на втором три. Найти вероятность того, что ровно одна изготовленная деталь бракованная.
3. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрыватся 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажутся 2 женщины?
4. В пирамиде 10 винтовок, из которых 7 снабжены оптическим прицелом. Вероятность поразить мишень из винтовки с оптическим прицелом равна 0,9; из винтовки без оптического прицела —0,7. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: он стрелял из винтовки с оптическим прицелом или без него?
5. Семь раз подбрасываются три игральные кости. Какова вероятность того, что сумма очков, равная 17, выпадет не более трех раз?
5.
Задачи на преобразование графиков
1. y = 4x + 8; 2. y = − x/3 + 2; 3. y = 3x − 2; 4. y = |x|; 5. y = |x|/x ; 6. y = 2|x + 1|; 7. y = −|5x + 2|; 8. y = |x| + 3; 9. y = |x| + x;
10. y = x 2 + |x| − 1; 11. y = 1/2 (|x + 1| − |x − 1|); 12. y = x 2 + 2;
13. y = −x 2 + 3; 14. y = 2x 2 + 1; 15. y = |4 − x 2 |; 16. y = −4x 2 + 1;
17. y = (x − 4)2 ; 18. y = −(x + 1)2 ; 19. y = (x + 2)2 − 1; 20. y = (x − 2)2 + 1; 21. y = 1 − 3(x − 3)2 ; 22. y = x 2 − 4x + 1; 23. y = x 2 − 5x + 6; 24. y = x 2 + 2x − 3; 25. y = 3x − x 2 ;
26. y = 2x 2 − 4x; 27. y = 4 − 2x 2 − 2x; 28. y = 4x − x 2 − 3;
29. y = 2|x| − x 2 ; 30. y = x|x − 1|; 31. y = |x 2 − 3x − 4|;
32. y = (x − 1)(1 − |x|); 33. y = |x − x 2 − 1|; 34. y = x n при n = 3, 4, 5, 1/2 , 1/3; 35. y = √ x + 1 36. y = √ 1 − 4x; 37. y = − √ 2x − 1;
38. y = 3√ 8x − 1; 39. y = 1 − 3√ 2x + 1; 40. y = k/x при k = 1, −1, 1/2 ;
41. y = 1/x + 2; 42. y = − 3/x − 1; 43. y = 3 – 4/x ;
44. y = 1 + 1/(x−2) ; 45. y = 2 – 3/(x+1); 46. y = 1/(x+3) − 1;
47. y = − 1/(x+2) − 3; 48. y = (x+5)/(x+3); 49. y = (5−2x)/(x−2);
50. y = (4x+7)/(2x−5); 51. y = (9x+4)/(3x+2); 52. y = (3−3x)/(2−6x);
53. y = (6x−2)/(x−1); 54. y = (7x+5)/(5x+6);
90. y = |log2 |3x + 4||; 91. y = sin ax при a = 1, 2, 2/3 , 1/2 ;
92. y = cos ax при a = 1, 1/2 , 4/3 ; 93. y = ctg ax при a = 1, 2, 1/2 , π;
94. y = tg ax при a = 1, 2, 1/2 , 3/2 , π; 95. y = cos (3/2) x + 1;
96. y = 1/4 tg πx/2 ; 97. y = 2 sin 3x + 1; 98. y = 1/2 cos πx − 1;
99. y = 1/4 ctg πx/4 ; 100. y = −2 sec x 2 , где sec x = 1/cos x ;
101. y = 1/2 cosec 2x, где cosec x = 1/sin x ; 102. y = 1 − 2 sin πx;
103. y = cos(x + π/6); 104. y = tg(π/4 – x) ; 105. y = 2sin(x – π/3) + 1;
107. y = 3 sin(2x + π/3); 108. y = −2 cos(x/2 + π/6); 109. y = 2 sin(πx – π/3);
6.
Задания для СР. Найти производные функции:
1. 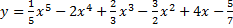 .
.
2. 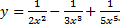
3. 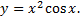
4. 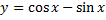 .
.
5. 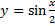 .
.
6. 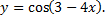
7. 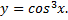
8. 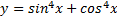 .
.
9. 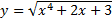 .
.
10. 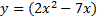 3.
3.
11. 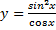 .
.
12. 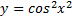 .
.
Задания для СР. Найти производные функции:
1. 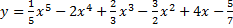 .
.
2. 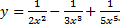
3. 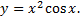
4. 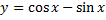 .
.
5. 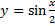 .
.
6. 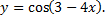
7. 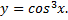
8. 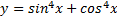 .
.
9. 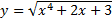 .
.
10. 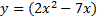 3.
3.
11. 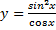 .
.
12. 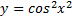 .
.
Дата добавления: 2019-09-13; просмотров: 377; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

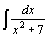 .
.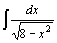 .
.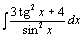 .
.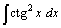 .
.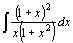 .
.