Понижение степени подынтегральной функции
Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы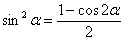 
, 
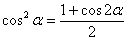и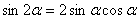 
, причем последняя формула чаще используется в обратном направлении: 
.
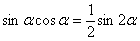Пример 7
Найти неопределенный интеграл.
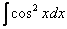
Решение:
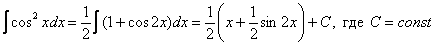
Пример 9
Найти неопределенный интеграл.
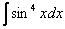
Сначала решение, потом комментарии:
Метод замены переменной
Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция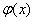 
и её производная 
:
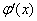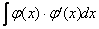(функции 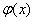, 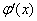не обязательно находятся в произведении)
Пример 11
Найти неопределенный интеграл.
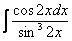
Прерываем решение и проводим замену
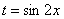
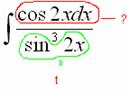
В знаменателе у нас всё хорошо, всё зависит только от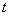 
, теперь осталось выяснить, во что превратится 
.
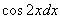Для этого находим дифференциал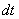 
:
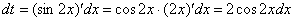
Или, если короче: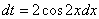 
Из полученного равенства по правилу пропорции выражаем нужное нам выражение:
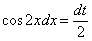
Итак:
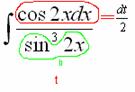
Теперь всё подынтегральное выражение у нас зависит только от 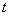и можно продолжать решение
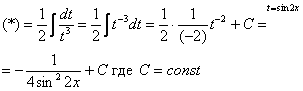
А сейчас два примера для самостоятельного решения:
Пример 12
Найти неопределенный интеграл.
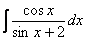
Пример 13
Найти неопределенный интеграл.
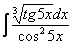
Пример 12: Решение:
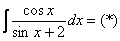
Проведем замену:
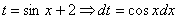
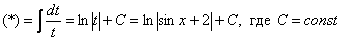
Примечание: здесь можно было сделать замену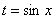 
, но гораздо выгоднее обозначить за 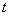весь знаменатель.
|
|
|
Пример 13: Решение:
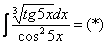
Проведем замену:
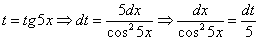
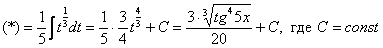
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: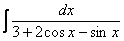 
, 
, 
, 
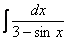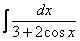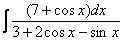и т.д.
Пример 17
Найти неопределенный интеграл.
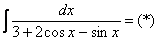
Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену: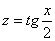 
. Я использую не букву 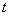, а букву 
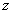, это не является каким-то правилом, просто опять же я так привык решать.
Здесь удобнее находить дифференциал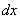 
, для этого из равенства 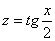, я выражаю 
:
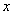Навешиваю на обе части арктангенс:
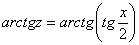
Арктангенс и тангенс взаимно уничтожаются:
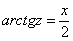
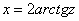
Таким образом:
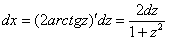
На практике можно не расписывать так подробно, а просто пользоваться готовым результатом: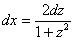 
! Выражение 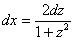справедливо только в том случае, если под синусами и косинусами у нас просто «иксы», для интеграла 
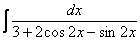(о котором мы еще поговорим) всё будет несколько иначе!
При замене 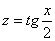синусы и косинусы у нас превращаются в следующие дроби:
, 
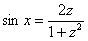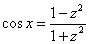, эти равенства основаны на известных тригонометрических формулах: 
, 
|
|
|
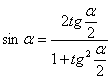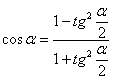
Итак, чистовое оформление может быть таким:
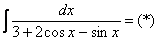
Проведем универсальную тригонометрическую подстановку: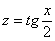 
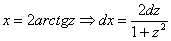
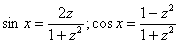
Дата добавления: 2019-09-13; просмотров: 1473; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!