Движение частицы в потенциальной яме
Рассмотрим движение частицы в потенциальной яме с бесконечно 
высокими стенками (рис. 20.5.1). Потенциальную энергию частицы в яме запишем в виде
,
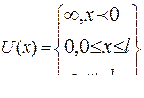здесь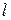 
-ширина потенциальной ямы.
Вероятность обнаружить частицу вне ямы равна нулю, тогда волновая функция, которая определяет вероятность нахождения частицы, равна нулю. Из свойства непрерывности волновой функции следует, что для волновой функции частицы на границе ямы можно написать
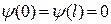. (20.5.1)
Внутри ямы потенциальная энергия частицы равна U = 0, тогда запишем уравнение Шредингера (20.4.3)для области внутри ямы (0 £ х £ l)
.
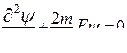Перепишем это уравнение в виде
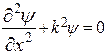, (20.5.2)
где квадрат волнового числа равен
. (20.5.3)
Решение дифференциального уравнения (20.5.2) запишем в общем виде
.
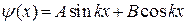Учтем ,что y(0) = 0, тогда В = 0, получим
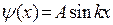. (20.5.4)
Учитывая соотношение (20.5.1), можно записать
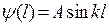= 0.
Соотношение выполняется при условии kl = n p , где n = 1, 2, 3,.. целые числа, тогда
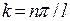. (20.5.5)
Подставляя формулу (20.5.5) в (20.5.3), найдем энергию частицы
|
|
|
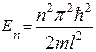. (20.5.6)
Энергия частицы в потенциальной яме принимает не любые, а только определенные дискретные (квантовые) значения. Эти квантовые значения энергии Е n называют энергетическими уровнями. Число п, соответствующее квантовым значениям энергии, называется главным квантовым числом.
Подставим формулу (20.5.5) в соотношение (20.5.4), получим
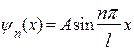. (20.5.7)
Постоянную А можно найти, подставив (20.5.7) в условие нормировки (20.3.1)
. (20.5.8)
Решая (20.5.8), получаем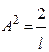 
, 
. Подставляя А в формулу (20.5.7), можно записать
. (20.5.9)
На рис. 20.5.2 приведены графики собственных функций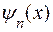 
, рассчитанные по формуле (20.5.9) для n = 1, 2 и 3. На рис. 20.5.3 приведены графики плотности вероятности расположения частицы в яме
.
В состоянии n = 1 частица чаще всего находится в середине ямы. В состоянии с n = 2 частица чаще находится в точках
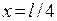и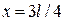 
.
Рис. 20.5.2 Рис. 20.5.3
|
|
|
Вероятность обнаружить частицу в середине ямы равна нулю. При n = 3 максимальна вероятность обнаружения частицы в точках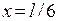 
, 
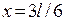и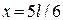 
.
Из формулы (20.5.6) можно определить расстояние между энергетическими уровнями
;
.
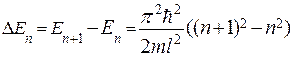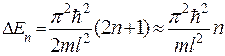При движении электрона в атоме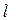 
~10-10 м, тогда 
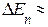10-17 n Дж.
Движению свободного электрона в металле можно сопоставить 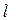~10-2 м, 
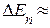10-35 nДж. Таким образом, чем больше ширина потенциальной ямы, тем меньше расстояние между энергетическими уровнями и спектр энергий можно считать непрерывным. Дискретность энергетических уровней проявляется в микромире, для которого необходимо применять квантовую механику.
Соотношение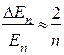 
показывает, что при больших квантовых числах n расстояние между уровнями уменьшается, т.е. дискретность квантовых уровней сглаживается, и законы квантовой механики переходят в законы классической физики при условии 
.
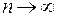Этот результат является частным случаем принципа соответствия Н. Бора (1923 г.), по которому законы квантовой механики при больших значениях квантовых чисел переходят в законы классической физики.
Дата добавления: 2019-09-13; просмотров: 279; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!