Критерий оценивания заданий 21–26.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | 2 |
| Имеется верное доказательство утверждения пункта а ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
| 27 |
Точки  и
и 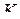 — соответственно середины сторон
— соответственно середины сторон  и
и 
квадрата  . Отрезки
. Отрезки  и
и  пересекаются в точке
пересекаются в точке  .
.
а) Докажите, что около четырёхугольника  можно описать окружность.
можно описать окружность.
б) Найдите  , если сторона квадрата равна 1.
, если сторона квадрата равна 1.
Решение.

|
а) Прямоугольные треугольники  и
и  равны
равны
по двум катетам. Значит,
 ,
,
то есть прямые  и
и  перпендикулярны. Значит,
перпендикулярны. Значит,
в четырёхугольнике  углы
углы  и
и  прямые, поэтому около него можно описать окружность.
прямые, поэтому около него можно описать окружность.
б) Прямоугольные треугольники  и
и  равны
равны
по двум катетам, значит,
 ,
,
то есть на хорды  и
и 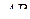 описанной около четырёхугольника
описанной около четырёхугольника  окружности опираются равные углы. Таким образом,
окружности опираются равные углы. Таким образом,  .
.
Ответ: б) 1.
| 28 |
Дана равнобедренная трапеция  с основаниями
с основаниями  и
и  Окружность
Окружность
с центром 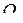 построенная на боковой стороне
построенная на боковой стороне  как на диаметре, касается боковой стороны
как на диаметре, касается боковой стороны  и второй раз пересекает большее основание
и второй раз пересекает большее основание  в точке
в точке  точка
точка 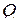 — середина
— середина 
а) Докажите, что четырёхугольник  — параллелограмм.
— параллелограмм.
|
|
|
б) Найдите  если
если  и
и  .
.
Решение.

|
а) Треугольник  равнобедренный, и трапеция
равнобедренный, и трапеция  равнобедренная, поэтому
равнобедренная, поэтому

Значит, прямые  и
и  параллельны, а так как
параллельны, а так как
 — средняя линия трапеции, то параллельны прямые
— средняя линия трапеции, то параллельны прямые  и
и  Противоположные стороны четырёхугольника
Противоположные стороны четырёхугольника  попарно параллельны, следовательно,
попарно параллельны, следовательно,  — параллелограмм.
— параллелограмм.
б) Пусть окружность с центром в точке  радиусом
радиусом  касается стороны
касается стороны 
в точке  В прямоугольных треугольниках
В прямоугольных треугольниках  и
и  :
:
 ,
, 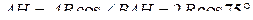 .
.
Поэтому  .
.
Пусть  Поскольку трапеция
Поскольку трапеция  равнобедренная,
равнобедренная,
 ;
;  .
.
Тогда  ,
,
откуда  . Значит,
. Значит,  .
.
Ответ: б) 3.
| 29 |
Точка  лежит на стороне
лежит на стороне  выпуклого четырёхугольника
выпуклого четырёхугольника  , причём
, причём  и
и  — вершины равнобедренных треугольников с основаниями
— вершины равнобедренных треугольников с основаниями  и
и  соответственно, а прямые
соответственно, а прямые  и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах  и
и  четырёхугольника
четырёхугольника  пересекаются на стороне
пересекаются на стороне  .
.
б) Пусть  — точка пересечения этих биссектрис. Найдите площадь четырёхугольника
— точка пересечения этих биссектрис. Найдите площадь четырёхугольника  , если известно, что
, если известно, что  , а площадь четырёхугольника, стороны которого лежат на прямых
, а площадь четырёхугольника, стороны которого лежат на прямых 

 и
и  равна 18.
равна 18.
Решение.

|
а) Пусть  — середина отрезка
— середина отрезка  Треугольник
Треугольник  равнобедренный, поэтому отрезок
равнобедренный, поэтому отрезок  является в нём медианой, биссектрисой и высотой. Поскольку прямые
является в нём медианой, биссектрисой и высотой. Поскольку прямые  и
и  перпендикулярны, прямая
перпендикулярны, прямая  содержит среднюю линию треугольника
содержит среднюю линию треугольника  , то есть проходит через середину стороны
, то есть проходит через середину стороны  Аналогично, биссектриса угла
Аналогично, биссектриса угла  тоже проходит через середину стороны
тоже проходит через середину стороны  Следовательно, биссектрисы углов
Следовательно, биссектрисы углов  и
и  четырёхугольника
четырёхугольника  пересекаются
пересекаются
на стороне 
|
|
|
б) Пусть прямые  и
и  пересекаются в точке
пересекаются в точке  а прямые
а прямые 
и  — в точке
— в точке  . Тогда четырёхугольник
. Тогда четырёхугольник  — прямоугольник. Площадь треугольника
— прямоугольник. Площадь треугольника 
 .
.
Аналогично,  Площадь треугольника
Площадь треугольника 
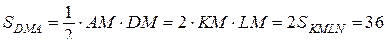 .
.
Тогда  .
.
Ответ: б) 96.
| 30 |
Точки  ,
,  и
и  — середины сторон соответственно
— середины сторон соответственно  ,
,  и
и  остроугольного треугольника
остроугольного треугольника  .
.
а) Докажите, что отличная от  точка пересечения окружностей, описанных около треугольников
точка пересечения окружностей, описанных около треугольников  и
и  , лежит на окружности, описанной около треугольника
, лежит на окружности, описанной около треугольника  .
.
б) Известно, что 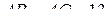 и
и  . Найдите радиус окружности, описанной около треугольника, вершинами которого являются центры окружностей, вписанных в треугольники
. Найдите радиус окружности, описанной около треугольника, вершинами которого являются центры окружностей, вписанных в треугольники  ,
,  и
и  .
.
Решение.
а) Пусть  — отличная от — отличная от  точка пересечения окружностей, описанных около треугольников точка пересечения окружностей, описанных около треугольников  и и  (рис. 1). Тогда (рис. 1). Тогда
 , ,
 ,
откуда ,
откуда
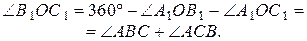 Значит,
Значит,
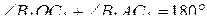 ,
следовательно, точки ,
следовательно, точки  , ,  , ,  и и  лежат на одной окружности. лежат на одной окружности.
| 
|
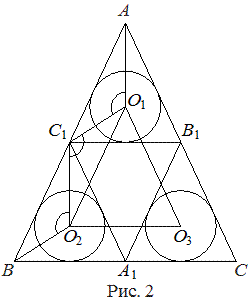
б) Пусть  , ,  и и  — центры окружностей, вписанных в треугольники — центры окружностей, вписанных в треугольники  , ,  и и  соответственно (рис. 2). Заметим, что соответственно (рис. 2). Заметим, что  , ,  как одинаковые элементы в равных треуголь-никах. Значит, треугольники как одинаковые элементы в равных треуголь-никах. Значит, треугольники  и и  равны. Кроме того, треугольник равны. Кроме того, треугольник  также равен этим треугольникам, поскольку также равен этим треугольникам, поскольку
 .
Таким образом, .
Таким образом,  . .
| 
|
Аналогично,  ,
,  , поэтому треугольник
, поэтому треугольник  подобен треугольнику
подобен треугольнику  с коэффициентом
с коэффициентом 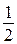 и радиус описанной около него окружности равен половине радиуса окружности, описанной около треугольника
и радиус описанной около него окружности равен половине радиуса окружности, описанной около треугольника  .
.
|
|
|
Пусть  — середина — середина  , а , а  и и  соответственно центр и радиус окружности, описанной около треугольника соответственно центр и радиус окружности, описанной около треугольника 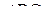 (рис. 3). Тогда высота равнобедренного треугольника (рис. 3). Тогда высота равнобедренного треугольника  равна равна  , поэтому из прямоугольного треугольника , поэтому из прямоугольного треугольника  получаем: получаем:
 ; ; 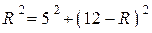 ; ;
 ; ;  .
Искомый радиус равен .
Искомый радиус равен  . .
| 
|
Ответ: б)  .
.
Дата добавления: 2019-09-13; просмотров: 146; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
