Критерии оценивания заданий 98–100
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 3 |
| Верно построена математическая модель, решение сведено к исследованию этой модели, и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано | 2 |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
| 101 |
Найдите все значения  , при каждом из которых система неравенств
, при каждом из которых система неравенств

имеет хотя бы одно решение.
Решение.
Заметим, что 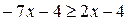 при
при 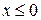 и
и 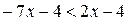 при
при 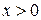 . Поэтому первое неравенство системы равносильно двойному неравенству
. Поэтому первое неравенство системы равносильно двойному неравенству 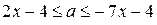 при
при 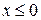 и равносильно двойному неравенству
и равносильно двойному неравенству 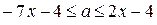 при
при 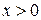 . При
. При 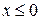 получаем:
получаем:
 ;
; 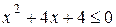 ;
; 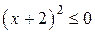 ,
,
откуда  . При
. При  исходная система принимает вид:
исходная система принимает вид:

откуда 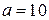 .
.
При любом 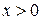 выполнено неравенство
выполнено неравенство  , поскольку
, поскольку 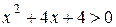 . Поэтому при
. Поэтому при 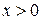 исходная система равносильна системе
исходная система равносильна системе

Из этой системы следует, что  , откуда
, откуда 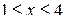 . Заметим, что максимальное значение функции
. Заметим, что максимальное значение функции  на отрезке
на отрезке 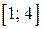 равно 4,
равно 4,
а минимальное значение функции 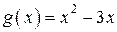 равно
равно 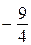 . Значит, выполнено неравенство
. Значит, выполнено неравенство 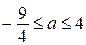 . Кроме того при
. Кроме того при 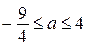 больший корень уравнения
больший корень уравнения  удовлетворяет системе неравенств, поскольку функция
удовлетворяет системе неравенств, поскольку функция 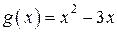 принимает на отрезке
принимает на отрезке  все значения от
все значения от 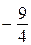
до 4, и её значения в каждой точке отрезка  не превосходят значений функции
не превосходят значений функции  . Таким образом, исходная система неравенств имеет хотя бы одно решение при
. Таким образом, исходная система неравенств имеет хотя бы одно решение при 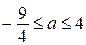 и
и 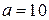 .
.
|
|
|
Ответ: 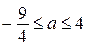 ;
; 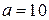 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 4 |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек  и / или и / или 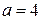
| 3 |
С помощью верного рассуждения получен промежуток 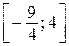 множества значений a, возможно, с исключением граничных точек, или точка множества значений a, возможно, с исключением граничных точек, или точка 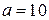 ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
| 2 |
Верно построено множество точек, координаты которых удовлетворяют системе неравенств,
ИЛИ
обоснованно получено множество значений параметра 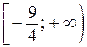 или или 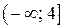
| 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
| 102 |
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
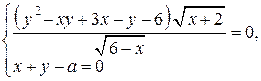
имеет ровно два различных решения.
Решение.
Запишем первое уравнение в виде
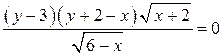 .
.
|
При  и
и  левая часть не имеет смысла. При
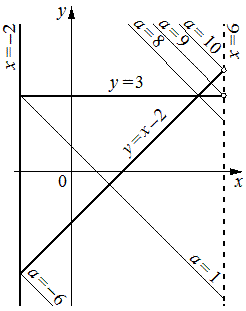
левая часть не имеет смысла. При  уравнение задаёт прямые
уравнение задаёт прямые 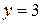 ,
, 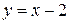 ,
, 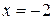 (см. рисунок).
(см. рисунок).
При каждом значении  уравнение
уравнение  задаёт прямую, параллельную прямой
задаёт прямую, параллельную прямой  или совпадающую с ней. При
или совпадающую с ней. При  такая прямая пересекает прямую
такая прямая пересекает прямую 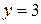 при
при 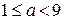 , пересекает прямую
, пересекает прямую 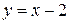 при
при  , пересекает прямую
, пересекает прямую 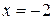 при любом значении
при любом значении  . При этом прямые
. При этом прямые  проходят через точки пересечения прямых
проходят через точки пересечения прямых 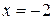 ,
, 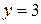 и
и 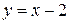 при
при 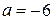 ,
, 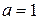 и
и 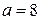 .
.
|
|
|
Число решений исходной системы равно числу точек пересечения прямых 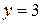 ,
, 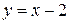 ,
, 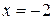 с прямой
с прямой  при условии
при условии  . Таким образом, исходная система имеет ровно два решения при
. Таким образом, исходная система имеет ровно два решения при 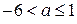 ;
; 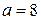 ;
;  .
.
Ответ:  ;
; 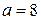 ;
; 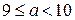 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 4 |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением/исключением точек 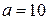 и/или и/или 
| 3 |
С помощью верного рассуждения получен один из промежутков множества значений a: 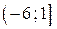 или или  , возможно, с включением/исключением граничных точек , возможно, с включением/исключением граничных точек
| 2 |
| Задача верно сведена к исследованию взаимного расположения прямых (аналитически или графически), ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
| 103 |
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений

имеет более двух решений.
Решение.
|
|
|
|
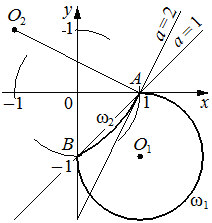
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая.
1) Если  , то получаем уравнение
, то получаем уравнение
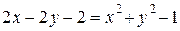 ;
;
 ;
;
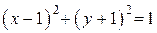 .
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом 1.
2) Если  , то получаем уравнение
, то получаем уравнение
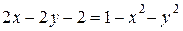 ;
;  ;
;  .
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом 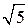 .
.
Полученные окружности пересекаются в двух точках — 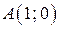 и
и 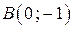 , лежащих на окружности
, лежащих на окружности 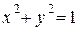 , поэтому в первом случае получаем дугу
, поэтому в первом случае получаем дугу 
с концами в точках 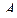 и
и  , во втором — дугу
, во втором — дугу 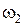 с концами в тех же точках (см. рисунок).
с концами в тех же точках (см. рисунок).
Рассмотрим второе уравнение системы. Оно задаёт прямую 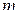 , которая проходит через точку
, которая проходит через точку  и угловой коэффициент которой равен
и угловой коэффициент которой равен  .
.
При  прямая
прямая 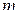 проходит через точки
проходит через точки  и
и 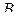 , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При 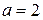 прямая
прямая 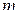 перпендикулярна прямой
перпендикулярна прямой 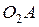 , угловой коэффициент которой равен
, угловой коэффициент которой равен 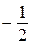 , значит, прямая
, значит, прямая 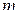 касается дуги
касается дуги 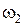 в точке
в точке  и пересекает дугу
и пересекает дугу  в двух точках (одна из которых — точка
в двух точках (одна из которых — точка  ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При 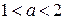 прямая
прямая 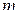 пересекает каждую из дуг
пересекает каждую из дуг  и
и 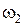 в точке
в точке  и ещё
и ещё
в одной точке, отличной от точки 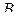 , то есть исходная система имеет три решения.
, то есть исходная система имеет три решения.
При 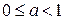 прямая
прямая 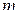 не пересекает дуги
не пересекает дуги 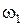 и
и 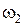 в точках, отличных
в точках, отличных
от точки 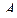 , то есть исходная система имеет одно решение.
, то есть исходная система имеет одно решение.
|
|
|
При  или
или 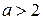 прямая
прямая 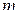 пересекает дугу
пересекает дугу 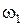 в двух точках и не пересекает дугу
в двух точках и не пересекает дугу 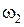 в точках, отличных от точки
в точках, отличных от точки  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
Значит, исходная система имеет более двух решений при 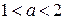 .
.
Ответ: 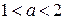 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 4 |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точки 
| 3 |
| При всех значениях a верно найдено количество решений системы в одном из двух случаев, возникающих при раскрытии модуля | 2 |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически), ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
| 104 |
Найдите все значения 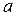 , при каждом из которых система уравнений
, при каждом из которых система уравнений

имеет ровно три различных решения.
Решение.

|
Запишем первое уравнение в виде
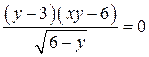 .
.
При 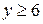 левая часть не имеет смысла.
левая часть не имеет смысла.
При  уравнение задаёт прямую
уравнение задаёт прямую 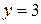
и гиперболу  (см. рисунок).
(см. рисунок).
При каждом значении 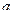 уравнение
уравнение  задаёт прямую, параллельную прямой
задаёт прямую, параллельную прямой  или совпадающую с ней.
или совпадающую с ней.
При  такая прямая пересекает прямую
такая прямая пересекает прямую 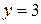 при любом значении
при любом значении  , пересекает правую ветвь гиперболы
, пересекает правую ветвь гиперболы 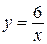 при
при  , пересекает левую ветвь гиперболы
, пересекает левую ветвь гиперболы  при любом значении
при любом значении  . При этом прямая
. При этом прямая 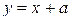 проходит через точку пересечения прямой
проходит через точку пересечения прямой 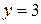 и гиперболы
и гиперболы 
при  .
.
Число решений исходной системы равно числу точек пересечения
прямой 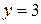 и гиперболы
и гиперболы  с прямой
с прямой 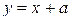 при условии
при условии  .
.
Таким образом, исходная система имеет ровно три решения при
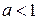 ;
; 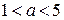 .
.
Ответ: 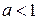 ;
; 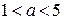 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 4 |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точки 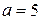
| 3 |
С помощью верного рассуждения получен один из промежутков множества значений a: 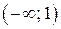 или или 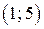 , возможно, с включением граничных точек , возможно, с включением граничных точек
| 2 |
| Задача верно сведена к исследованию взаимного расположения гиперболы и прямых (аналитически или графически), ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
| 105 |
Саша берёт пять различных натуральных чисел и проделывает с ними следующие операции: сначала вычисляет среднее арифметическое первых двух чисел, затем — среднее арифметическое полученного результата
и третьего числа, потом среднее арифметическое полученного результата
и четвёртого числа и в конце — среднее арифметическое полученного результата и пятого числа — число 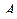 .
.
а) Может ли число 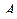 равняться среднему арифметическому изначальных пяти чисел?
равняться среднему арифметическому изначальных пяти чисел?
б) Может ли число 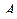 быть больше среднего арифметического изначальных пяти чисел в 5 раз?
быть больше среднего арифметического изначальных пяти чисел в 5 раз?
в) В какое наибольшее целое число раз число 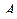 может быть больше среднего арифметического изначальных пяти чисел?
может быть больше среднего арифметического изначальных пяти чисел?
Решение.
а) Например, для чисел 1, 3, 8, 11 и 2 число 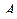 равно их среднему арифметическому.
равно их среднему арифметическому.
б) Пусть изначальные числа равны  ,
,  ,
, 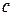 ,
, 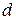 и
и 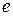 . Тогда
. Тогда  , а среднее арифметическое этих чисел равно
, а среднее арифметическое этих чисел равно 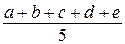 . Если число
. Если число 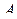 больше среднего арифметического в 5 раз, то
больше среднего арифметического в 5 раз, то
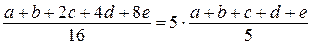 ;
;  ,
,
откуда 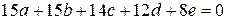 , что невозможно.
, что невозможно.
в) Предположим, что число 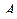 в
в 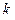 раз больше среднего арифметического пяти чисел, тогда
раз больше среднего арифметического пяти чисел, тогда
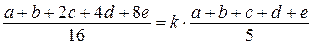 ;
; 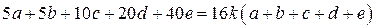 ,
,
откуда 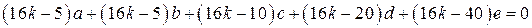 , что невозможно при
, что невозможно при 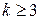 .
.
Для чисел 1, 3, 4, 7 и 35 число 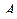 вдвое больше их среднего арифметического.
вдвое больше их среднего арифметического.
Таким образом, число 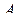 может быть вдвое больше среднего арифметического, но не может быть больше в большее целое число раз.
может быть вдвое больше среднего арифметического, но не может быть больше в большее целое число раз.
Ответ: а) да; б) нет; в) 2.
| 106 |
а) Приведите пример четырёхзначного числа, произведение цифр которого
в 10 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого
в 175 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа.
Решение.
а) Произведение цифр числа 2529 равно 180, а сумма цифр равна 18, то есть
в 10 раз меньше.
б) Предположим, что такое число 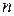 существует и
существует и  ,
,  ,
, 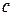 ,
, 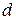 — его цифры. Заметим, что среди этих цифр не может быть нулей, так как иначе
— его цифры. Заметим, что среди этих цифр не может быть нулей, так как иначе
их произведение было бы равно нулю. Имеем:  . Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две
. Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две
цифры «5». Так как при перестановке местами цифр числа 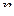 равенство
равенство  остаётся верным, то без ограничения общности можно считать, что в числе
остаётся верным, то без ограничения общности можно считать, что в числе 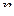 цифры
цифры 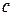 и
и 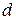 равны 5.
равны 5.
Тогда 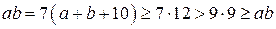 . Получаем противоречие.
. Получаем противоречие.
в) Предположим, что такое число 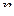 существует и
существует и  ,
,  ,
, 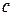 ,
, 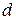 — его цифры. Как и выше, заметим, что среди этих цифр не может быть нулей, так как иначе их произведение было бы равно нулю. Имеем:
— его цифры. Как и выше, заметим, что среди этих цифр не может быть нулей, так как иначе их произведение было бы равно нулю. Имеем: 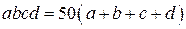 . Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две
. Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две
цифры «5». Без ограничения общности будем считать, что 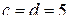 .
.
Тогда  . Так как правая часть последнего равенства делится
. Так как правая часть последнего равенства делится
на 2, то либо  , либо
, либо  делится на 2. Будем считать, что на 2 делится
делится на 2. Будем считать, что на 2 делится  .
.
Если 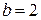 , то
, то 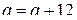 , что невозможно.
, что невозможно.
Если 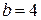 , то
, то  ;
; 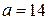 , что невозможно.
, что невозможно.
Если  , то
, то  ;
; 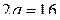 ;
; 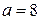 . Число
. Число 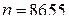 и все числа, получаемые из него перестановкой цифр, удовлетворяют условию задачи.
и все числа, получаемые из него перестановкой цифр, удовлетворяют условию задачи.
Если 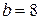 , то
, то  ;
;  ;
; 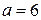 . Этот вариант также получается
. Этот вариант также получается
из предыдущего перестановкой цифр.
Ответ: а) например, 2529; б) нет; в) число 8655 и все числа, получаемые
из него перестановкой цифр (всего 12 чисел).
| 107 |
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы
в каждой группе было хотя бы одночисло. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы
из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
Решение.
а) Например, для групп  и
и  средние значения совпадают
средние значения совпадают
и равны 7.
б) Допустим, что это возможно. Пусть все средние значения равны 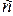 .
.
В каждой группе от 1 до 8 натуральных чисел, поэтому 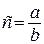 , где
, где 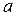 — натуральное число и
— натуральное число и  . Пусть группы состоят из
. Пусть группы состоят из 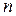 ,
, 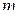
и 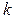 чисел. Тогда суммы чисел в группах равны
чисел. Тогда суммы чисел в группах равны 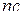 ,
, 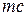 и
и 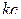 соответственно, а общая сумма всех 10 чисел равна 61 и равна
соответственно, а общая сумма всех 10 чисел равна 61 и равна  . Поэтому
. Поэтому 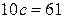 ;
; 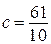 . Это противоречит тому, что знаменатель числа
. Это противоречит тому, что знаменатель числа 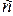 не превосходит 8.
не превосходит 8.
в) Пусть группы состоят из 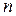 ,
, 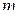 и
и 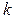 чисел, а средние значения равны
чисел, а средние значения равны  ,
, 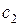
и 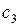 соответственно. Если
соответственно. Если 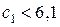 ,
,  ,
, 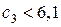 , то
, то
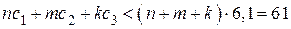 ,
,
что противоречит условию. Значит, хотя бы одно из чисел  ,
, 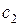 ,
, 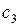
не меньше 6,1. Поэтому максимальное из этих чисел не меньше 6,1. При этом каждое из этих чисел имеет вид  , где
, где 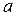 — натуральное число
— натуральное число
и  , поэтому максимальное из этих чисел не меньше
, поэтому максимальное из этих чисел не меньше 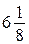 .
.
Покажем, что максимальное из этих чисел не может равняться 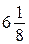 .
.
Пусть 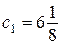 . Тогда первая группа состоит из 8 чисел, сумма которых
. Тогда первая группа состоит из 8 чисел, сумма которых
равна  . Значит, каждая из других двух групп состоит из одного числа, причём сумма двух чисел из второй и третьей групп равна 12.
. Значит, каждая из других двух групп состоит из одного числа, причём сумма двух чисел из второй и третьей групп равна 12.
Но тогда одно из этих чисел больше 6, поэтому максимальное среднее больше  . Получаем, что максимальное из чисел
. Получаем, что максимальное из чисел  ,
,  ,
, 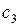 не меньше
не меньше 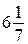 .
.
Покажем, что максимальное из чисел  ,
, 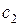 ,
, 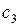 может равняться
может равняться 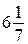 . Например, для разбиения на группы
. Например, для разбиения на группы  ,
, 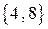 ,
, 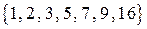 получаем:
получаем: 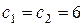 ,
, 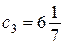 .
.
Ответ: а) да; б) нет; в) 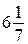 .
.
Дата добавления: 2019-09-13; просмотров: 285; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
