Действующее и среднее значение периодической несинусоидальной величины

 

Периодический несинусоидальный ток по аналогии с током синусоидальным может быть охарактеризован эффективным или действующим значением. В разделе 3.2 действующее значение периодической величины определялось в общем виде (3.7) как ее среднеквадратичное значение за период:

 

I =			1	∫T	i2(t )dt .	(4.8)
			T
		0
Используя представление негармонического тока i(t) рядом Фурье (4.2), т.е.
выражением
	∞
i = I0+	∑	I km sin(k ω t +ψ ik ),				(4.9)

 

n=1

подынтегральную функцию i² (t ) в формуле (4.8) запишем следующим образом:

∞	∞
i2(t )= I02+ I0∑I km sin(k ω t +ψ ik )+∑I km2 sin2		(k ω t +ψ ik )+
k =1	k =1

 

 

98

	∞	∞
+	∑∑		I km I nm sin(k ω t +ψ ik ) sin(n ω t +ψ in ).	(4.10)

 

k =1 n=1

В≠n

 

Подставляя соотношение (4.10) в формулу (4.8), после несложных преобразований получим

∞

I ²= I ²+¹∑I ²

_{0  2          km}

 

или

 

∞

I = ∑I _k²

 

k =0

 

где I₁ = I_1m  2 , I₂ = I_2m  2 , K ,

 

представляющих ряд (4.9).

 

= I02+ I12+ I22+K+ I k2+K,

(4.11)

 

I _k = I _km  2 K — действующие значения гармоник,

 

Таким образом, действующее значение периодического несинусоидального тока согласно (4.11) равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.

 

Аналогичным образом, исходя из представления напряжений и ЭДС, т.е. функций u(t )и e(t ),рядами Фурье(4.6),на основании формул(3.8)можно доказать,чтодействующие значения несинусоидальных напряжений и ЭДС равны:

	∞			∞
U =	∑U k2, E =			∑E k2,	(4.12)
	k =0			k =0
где U k = U km 2 и E k = E km	2 ( k =		) —	действующие значения	гармоник
		1,∞

напряжения и ЭДС.

 

Средним значением периодической несинусоидальной величины(средневыпрямленным значением) называют ее среднее значение за половину периода. Так, например, среднее значение силы тока

T 2
I ср = T2∫i(t )dt .	(4.13)

0

 

Так же определяются средние значения напряжения и ЭДС:

	2	T 2		2	T 2
U ср =		∫u(t )dt ,	E ср =		∫e(t )dt .	(4.14)
	T			T
0			0

Отметим, что любой из интегралов (4.13), (4.14) равен среднему по модулю значению величины за период, если каждая из этих величин, например, i(t), имеет одинаковые положительные и отрицательные полуволны:

		T						T 2
I ср =	1	∫		i(t )		dt =	2	∫i(t )dt .
	T						T
0								0

Примечания

 

1 Из формул (4.6), представляющих разложения периодических токов, напряжений и ЭДС в ряды Фурье, и из выражений (4.4) для коэффициентов этих

 

99

разложений следует, что средние за период значения несинусоидальных величин совпадают с нулевыми гармониками (с постоянными составляющими):

I0=	1	∫T i(t )dt ,	U0=	1	∫T u(t )dt ,	E0=	1	∫T e(t )dt .
	T			T			T
0			0			0

2 Измерение несинусоидальных токов, напряжений и ЭДС приборами различных систем может давать неодинаковые результаты.

 

Приборы электродинамической, электромагнитной и тепловой систем реагируют на действующие значения измеряемой величины. Магнитоэлектрические приборы сами по себе измеряют постоянную составляющую,а с выпрямителями—среднее по модулю значение.

 

4.4 Коэффициенты,            характеризующие            форму           периодических

 

Несинусоидальных величин

При оценке формы периодических несинусоидальных величин используют следующие характеристики: коэффициент формы k _ф , коэффициент амплитуды k _а ,

 

коэффициент искажения k _и и коэффициент гармоник k _г .

 

Коэффициент формы определяется как отношение действующего значения ксреднему по модулю значению, например, для силы тока:

k ф =	I	.	(4.15)
	I ср

Коэффициент амплитуды равен отношению максимального значения величины кее действующему значению:

k а =	I max	.	(4.16)
	I

Коэффициент искажения определяется как отношение действующего значенияосновной гармоники к действующему значению всей величины:

k и	=	I1	.	(4.17)
		I

Коэффициент гармоник равен отношению действующего значения высшихгармоник к действующему значению основной гармоники:

∞

∑I _k²

k =   ^{k =2}    .                                                                         (4.18)

_г          ^I1

Примечание –Для синусоидальных токов вышеуказанные характеристики

равны: k _ф = π 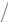(2 2 )≈ 1.11, k _а =  2 ≈ 1.41, k _и = 1 и k _г = 0 .

 

---

Дата добавления: 2019-07-15; просмотров: 384; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!