Лекция 7. Нелинейные электрические цепи постоянного тока
7.1 Нелинейные электрические цепи и элементы. Основные понятия
Основными параметрами пассивных элементов электрических цепей являются сопротивление R , индуктивность L и ёмкость C . Эти параметры, строго говоря,
зависят от тока или напряжения, т.е. представимы функциями вида R = R(i,u),
L = L(i,u) и C = C(i,u). На практике указанные зависимости задают тремя типами
характеристик — вольт-амперной, вебер-амперной и кулон-вольтной.
Зависимость силы тока в элементе цепи от напряжения на нем, т.е. функция
i = i(u), называется вольт-амперной характеристикой (рисунок 7.1, а).
Зависимость потокосцепления элемента цепи от тока в нем, т.е. функция
Y =Y (i), называется вебер-амперной характеристикой (рисунок 7.1, б).
Зависимость заряда элемента цепи от напряжения на нем, т.е. функция q = q(u),
называется кулон-вольтной характеристикой (рисунок 7.1, в).
 |  |  |
а) б) в)
Рисунок 7.1 – Вольт-амперная (а), вебер-амперная (б) и кулон-вольтная (в) характеристики линейных (кривые 1) и нелинейных (кривые 2) элементов цепи
Элементы цепи, параметры R , L и C которых не зависят от тока или
напряжения, называются линейными. Характеристики i = i(u), Y =Y (i) и q = q(u)
линейных элементов изображаются прямыми линиями (кривые 1 на рисунке 7.1).
Элементы цепи параметры R , L и C которых зависят от тока или напряжения,
называются нелинейными. Характеристики i = i(u), Y =Y (i) и q = q(u) нелинейных
элементов не являются прямыми линиями (кривые 2 на рисунке 7.1).
Электрическая цепь, в которой есть хотя бы один нелинейный элемент, называется нелинейной электрической цепью.
Для математического описания процессов в нелинейных электрических цепях в соответствующие схемы замещения вводят те же идеализированные пассивные элементы, что и в случае линейных цепей, т.е. резистивный, индуктивный и ёмкостный. Эти элементы называются соответственно нелинейное сопротивление (нелинейный резистор), нелинейная индуктивность (нелинейная катушка) и нелинейная ёмкость (нелинейный конденсатор). Условные обозначения нелинейных пассивных элементов представлены на рисунке 7.2.



а) б) в)
Рисунок 7.2 – Условные графические обозначения нелинейных резистивного (а),
индуктивного (б) и ёмкостного (в) элементов на схемах замещения
Примечание – Каждая из функций
i = i(u), Y =Y (i) и
q = q(u)
сопоставляется
соответствующему идеализированному пассивному элементу цепи. Так, например,
функция i = i(u) является характеристикой нелинейного резистора, функция Y =Y (i)
— характеристикой нелинейной индуктивной катушки, функция q = q(u) —
характеристикой нелинейного конденсатора.
7.2 Нелинейные электрические цепи постоянного тока и нелинейные сопротивления. Классификация нелинейных элементов цепи
При постоянном токе неизменными во времени являются потокосцепления и заряды, поэтому индуцируемые в цепи ЭДС и токи в конденсаторах равны нулю. По этой причине распределение токов и напряжений в схемах определяется резисторами, активными сопротивлениями обмоток индуктивных катушек и активными проводимостями неидеальных конденсаторов. Таким образом, нелинейную электрическую цепь в отношении постоянного тока следует рассматривать как цепь резистивную, основными параметрами которой являются сопротивления R и проводимости g ветвей с нелинейными резистивными элементами.
Основной характеристикой нелинейного сопротивления в цепи постоянного тока
является его вольт-амперная характеристика (ВАХ), т.е. функция обратная зависимость U = U (I ).
I = I (U ), а также
Вольт-амперные характеристики могут быть заданы в виде графиков, таблиц и аналитических выражений. Наиболее полное описание ВАХ дают аналитические зависимости, так как и графическая и табличная формы задания ВАХ недостаточно точны и имеют ограниченный диапазон изменения силы тока и напряжения.
Все нелинейные элементы в зависимости от признака классификации можно разбить на следующие основные группы:
1) двухполюсные и многополюсные;
2) инерционные и безынерционные;
3) симметричные и несимметричные;
4) с однозначной и неоднозначной ВАХ;
5) управляемые и неуправляемые.
Рассмотрим подробнее каждый из признаков классификации.
7.2.1 Двухполюсные и многополюсные элементы
В зависимости от количества полюсов, с помощью которых нелинейные элементы подключается к электрической цепи, их можно разделить на двух- и многополюсные. К двухполюсным элементам, например, относятся полупроводниковый и электровакуумный диоды. Примерами многополюсных элементов являются различные полупроводниковые и электровакуумные триоды, магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.
7.2.2 Инерционные и безынерционные элементы
В зависимости от скорости изменения тока или напряжения нелинейные элементы подразделяются на инерционные и безынерционные. Если ВАХ нелинейного
резистивного элемента для изменяющегося во времени тока i = i(u) и постоянного тока
I = I (U ) совпадают, то такой элемент называют безынерционным, в противном случае
инерционным. Проявлением инерционности у нелинейных резисторов является невозможность быстрого изменения их сопротивления. Таким свойством, в частности, обладают лампы накаливания со значительной тепловой инерцией. Электронные лампы, напротив, при не слишком высоких частотах могут рассматриваться как безынерционные элементы.
7.2.3 Симметричные и несимметричные элементы
По виду вольт-амперной характеристики различают симметричные и несимметричные элементы.
Симметричными называют нелинейные элементы, вольт-амперные характеристики которых не зависят от направления тока или напряжения на зажимах. К симметричным нелинейным элементам относят электрические лампы (рисунок 7.3, а), терморезисторы (рисунок 7.3, б).
 |  |
а) б)
Рисунок 7.3 – Вольт-амперные характеристики симметричных элементов: электрической лампы (а) и терморезистора (б)
Несимметричными называют нелинейные элементы, вольт-амперные характеристики которых не одинаковы при различных направлениях тока или напряжения на зажимах.
 |  |
а) б)
Рисунок 7.4 – Вольт-амперные характеристики несимметричных элементов: полупроводникового диода (а) и электрической дуги (б)
К несимметричным элементам относят полупроводниковые диоды (рисунок 7.4, а),
электрическую дугу с разнородными электродами (рисунок 7.4, б)
7.2.4 Элементы с однозначной и неоднозначной характеристиками
С точки зрения однозначного и неоднозначного взаимного отображения токов и напряжений нелинейные элементы делят на элементы с однозначной и неоднозначной характеристиками.
Однозначной (монотонной) называется ВАХ, у которой каждому значению тока соответствует единственное значение напряжения и наоборот (рисунок 7.5, а).


а) б)


в) г)
Рисунок 7.5 – Вольт-амперные характеристики с однозначной (а) и неоднозначной (б) – (г)
зависимостями между током и напряжением
В случае неоднозначной ВАХ одному значению тока может соответствовать два и более значений напряжения и наоборот. Неоднозначные вольт-амперные характеристики подразделяют на следующие виды:
1) Управляемая напряжением ВАХ, для которой заданные напряжения в каждой точке характеристики однозначно определяют токи, но при заданном токе напряжения определяются неоднозначно (рисунок 7.5, б).
2) Управляемая током ВАХ, для которой заданные токи в каждой точке характеристики однозначно определяют напряжения, но при заданном напряжении токи определяются неоднозначно (рисунок 7.5, в).
3) Неуправляемая ВАХ, для которой характерна многозначность и тока, и напряжения (рисунок 7.5, г).
7.2.5 Управляемые и неуправляемые элементы
По возможности управления все нелинейные элементы делят на управляемые и неуправляемые. Управляемые элементы (в отличие от неуправляемых) содержат
специальные (управляющие) каналы, изменяя напряжение, ток, световой поток и др. в которых изменяют их основные характеристики: вольт-амперную, вебер-амперную и кулон-вольтную. Примером управляемого элемента является полупроводниковый транзистор.
7.3 Параметры нелинейных резисторов в цепи постоянного тока. Понятие о статическом, дифференциальном и динамическом сопротивлении
Поскольку у нелинейных резисторов отсутствует прямая пропорциональность между напряжением и током, их нельзя охарактеризовать одним параметром (сопротивлением R или проводимостью g ). Соотношения между этими величинами в
общем случае зависят не только от их мгновенных значений, но и от производных и интегралов по времени.
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления. Если нелинейный элемент является безынерционным, то он характеризуется первыми двумя из перечисленных параметров.
Статическим сопротивлением нелинейного элемента (или сопротивлением постоянному току) называется отношение напряжения на резистивном элементе к величине протекающего через него тока в данной точке вольт-амперной характеристики:
R ст
= U . (7.1)
 I
I
Дифференциальным сопротивлением нелинейного элемента называется предел отношения приращения напряжения на резистивном элементе к приращению протекающего через него тока, или, другими словами, производная от напряжения по току в данной точке вольт-амперной характеристики:
|
Ä I ®0 Ä I
= dU
 dI
dI
. (7.2)

Рисунок 7.6 – Определение статического и дифференциального сопротивления нелинейного элемента на вольт-амперной характеристике
Обозначим через m I
и m U
масштабы тока и напряжения на вольт-амперной
характеристике. Из формул (7.1) и (7.2) тогда следует, что статическое сопротивление
R ст
пропорционально тангенсу угла наклона прямой, проведенной из начала координат
в данную точку « a » характеристики, а дифференциальное сопротивление R д
пропорционально тангенсу угла наклона касательной в данной точке « a »
характеристики (рисунок 7.6):
где
m R = m U
 m I .
m I .
R ст = m R tg a ,
R д = m R tg b , (7.3)
Примечания
1 Статическое сопротивление пассивного элемента всегда положительно, т.е. R ст > 0 ; дифференциальное сопротивление может быть как положительным, так и отрицательным, т.е. является величиной алгебраической. Положительным ( R д > 0 ) дифференциальное сопротивление будет в точках ВАХ, лежащих на ее восходящей части (участки « ab » и « cd » на рисунке 7.7), и отрицательным ( R д < 0 ), если рассматриваемые точки расположены на нисходящих участках ВАХ (участок « bc » на рисунке 7.7).
 |
Рисунок 7.7 – Определение знака дифференциального сопротивления на различных участках вольт-амперной характеристики нелинейного элемента
2 Наряду со статическим и дифференциальным сопротивлениями, т.е. функциями
R ст
и R д , параметры нелинейного резистивного элемента иногда представляют
статической и дифференциальной проводимостями, определяемыми следующим соотношениями:
g = I ,

g = lim
Ä I = dI

. (7.4)
ст U

д Ä U ®0 Ä U dU
3 В случае инерционного нелинейного резистора вводится понятие динамического сопротивления (сопротивления переменному току)
R = lim Äu = du , (7.5)

дин Ä i®0 Ä i di
определяемого по динамической ВАХ. В зависимости от скорости изменения тока или напряжения может изменяться не только величина, но и знак R дин .
7.4 Основные особенности и общая характеристика методов расчета нелинейных электрических цепей постоянного тока
Расчет любой электрической цепи (линейной или нелинейной) сводится либо к нахождению токов и напряжений по заданным параметрам цепи и источников (задача анализа), либо к определению параметров цепи по заданным характеристикам (задача синтеза).
Для расчета линейных электрических цепей существуют различные методы (контурных токов, узловых потенциалов, символический, операторный и др.), которые позволяют анализировать любую цепь в стационарном или переходном режиме. Расчет нелинейных электрических цепей имеет ряд особенностей.
7.4.1 Основные особенности расчета нелинейных электрических цепей постоянного тока
1) Электрическое состояние нелинейной цепи постоянного тока так же, как и линейной цепи, описывается системой алгебраических уравнений, составленных по 1-му и 2-му законам Кирхгофа. Правила составления системы уравнений Кирхгофа одинаковы для линейной и нелинейной цепи. Однако электрическое состояние нелинейной цепи описывается системой нелинейных алгебраических уравнений. Как известно, общих аналитических методов решения нелинейных уравнений не существует, поэтому в общем случае решение таких задач осуществляется численными методами математики с использованием современных ЭВМ.
2) К нелинейным цепям неприменим принцип наложения (суперпозиции), поэтому методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.
Нарушение принципа наложения продемонстрируем на примере нелинейного
элемента, в котором ток пропорционален квадрату напряжения: коэффициент пропорциональности.
I = kU 2 , где k —
Если в цепи действуют два последовательно соединенных источника с напряжениями U1 и U2 , то токи, вызываемые каждым из них в отдельности (частичные
токи), равны:
I = kU 2 и I = kU 2 . Ток при одновременном действии обоих источников
1 1 2 2
определяется формулой
I = k(U
+ U )2 = kU 2 + 2kU U + kU 2 ,
1 2 1 1 2 2
согласно которой результирующий ток I не равен сумме частичных токов
I1 и
I2 .
3) Вольт-амперные характеристики нелинейных элементов в большинстве случаев определяются экспериментально и задаются в виде графиков, представляющих собой кривые линии, аналитические выражения которых неизвестны, причем разные виды нелинейных элементов имеют разные характеристики. Многообразие этих характеристик обусловливает трудность расчета нелинейных электрических цепей и использование различных методов.
4) При наличии экспериментально снятой характеристики, аналитическое выражение которой неизвестно, для расчета нелинейной цепи можно применять только графические методы, которые не всегда позволяют сделать общие выводы. Эта трудность может быть преодолена путем аппроксимации экспериментальной характеристики аналитическим выражением.
цепей
7.4.2 Общая характеристика методов расчета нелинейных электрических
Все многообразие методов расчета нелинейных электрических цепей можно
свести к трем основным группам:
1) графические методы, осуществляемые геометрическими построениями на основе заданных характеристик. Эти методы обладают большой наглядностью, дают вполне удовлетворительную точность решения, которая зависит в основном от
стабильности характеристик нелинейного элемента и тщательности выполнения графических работ;
2) аналитические методы, основанные на том, что характеристика нелинейного элемента выражается приближенно аналитической функцией. Аналитический метод обычно менее нагляден, но с его помощью удается получить общие расчетные зависимости;
3) численные методы, основанные на приближенных способах решения алгебраических и дифференциальных уравнений с помощью ЭВМ.
Кроме того, в практике расчета нелинейных цепей широко используются
комбинированные методы (например, графо-аналитические).
7.5 Графические методы расчета нелинейных цепей
При использовании графических методов расчета задача решается путем графических построений на плоскости. При этом характеристики всех ветвей схемы следует записать в функции одного общего аргумента. Благодаря этому система уравнений сведется к одному нелинейному уравнению с одним неизвестным.
7.5.1 Метод эквивалентных преобразований при последовательном соединении нелинейных сопротивлений
Метод эквивалентных преобразований был рассмотрен в разделе 2.6.2 в применении к линейным цепям постоянного тока. Этот метод основан на замене нескольких элементов одним эквивалентным. Аналогичные эквивалентные преобразования могут быть осуществлены и в нелинейной цепи.
Пусть электрическая цепь (рисунок 7.8, а) состоит из двух последовательно
соединенных нелинейных резисторов R1 и R2 , вольт-амперные характеристики
которых, т.е. функции I = I1(U ) и I = I2 (U ), известны (рисунок 7.8, б). Требуется
определить значение тока I в цепи и величину напряжений сопротивлений при заданном значении ЭДС источника E .
U1, U2
на каждом из



а) б) в)
Рисунок 7.8 – Последовательное соединение нелинейных сопротивлений (а) и графическая интерпретация метода эквивалентных преобразований (б), (в)
Решить поставленную задачу, применив непосредственно закон Ома, не представляется возможным, так как сопротивления нелинейных элементов зависят от тока. Задача может быть решена, если два элемента цепи рисунка 7.8, а заменить эквивалентным, преобразовав ее к виду схемы рисунка 7.8, в. Вольт-амперная
характеристика
I = I (U )
эквивалентного нелинейного сопротивления R
(результирующая ВАХ) определяется из соотношений
I1 = I2 = I = const ,
и может быть получена графическим путем.
U = U1 + U 2
(7.6)
Из уравнений (7.6) следует, что при последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Это означает, что результирующую ВАХ
можно построить путем суммирования абсцисс вольт-амперных характеристик
I = I1(U ) и I = I2 (U ) элементов R1 и R2 при фиксированных значениях тока I .
Графическая интерпретация указанных построений приведена на рисунке 7.8, б.
Здесь для некоторого значения силы тока
I = I a , задаваемого точкой « a » на оси
ординат, показано правило определения точки « d », принадлежащей результирующей
ВАХ I = I (U ) последовательного соединения сопротивлений R1 и R2 . Как следует из
рисунка, положение точки « d » при фиксированном значении тока на основании графического уравнения



I = I a
определяется
ab + ac = ad , (7.7)


где отрезки ab и ac выражают в заданном масштабе m U
напряжения
U1a
и U2a на
элементах
R1 и
R2 , соответствующие выбранному значению тока

I a , а отрезок ad —
напряжение U a
на эквивалентном сопротивлении R при том же значении тока:

U1a = m U × ab ,

U2a = m U × ac ,

U a = m U × ad . (7.8)
Таким образом, графическое уравнение (7.7) соответствует 2-му закону Кирхгофа
U = U1 + U 2 .
Для определения величины тока I при заданном по условию задачи значении
ЭДС E на оси напряжений откладывается точка « m¢», соответствующая в выбранном масштабе величине ЭДС E , из которой восстанавливается перпендикуляр до
пересечения с зависимостью I = I (U ) (на рисунке 7.8, б — это точка « m »). Из точки
пересечения перпендикуляра с кривой I = I (U ), т.е. из точки « m », опускается
ортогональ на ось токов — полученная точка « m¢ » соответствует искомому току
I = I (E ) в цепи. Абсциссы точек пересечения ортогонали с зависимостями I = I1(U ) и
I = I2 (U ) определяют напряжения U1 и U 2 на последовательно соединенных
резисторах
R1 и R2
(рисунок 7.8, б).
Примечание – Рассмотренный прием может быть обобщен на любое число нелинейных сопротивлений, соединенных последовательно.
7.5.2 Метод эквивалентных преобразований при параллельном соединении нелинейных сопротивлений
Пусть электрическая цепь (рисунок 7.9, а) состоит из 2-х параллельно
соединенных нелинейных резисторов R1 и R2 , вольт-амперные характеристики
которых, т.е. функции I = I1(U ) и I = I2 (U ), известны (рисунок 7.9, б). Требуется
определить значение тока I в неразветвленной части цепи, а также величины токов
I1 и
I2 в параллельных ветвях с сопротивлениями
R1 и R2
при заданном значении ЭДС
источника E .


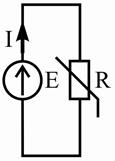
а) б) в)
Рисунок 7.9 – Параллельное соединение нелинейных сопротивлений (а) и графическая интерпретация метода эквивалентных преобразований (б), (в)
Как и в случае последовательного соединения нелинейных сопротивлений, решение задачи сводится к преобразованию исходной схемы, изображенной на рисунке 7.9, а, к эквивалентной схеме рисунка 7.8, в и, следовательно, к определению результирующей ВАХ параллельного соединения. Методика построения этой ВАХ принципиально ничем не отличается от ранее рассмотренной. Только в данном случае в основе ее построения лежат уравнения
I = I1 + I2 , U = U1 = U 2 = const . (7.9)
Из уравнений (7.9) следует, что при параллельном соединении нелинейных
резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Это означает, что результирующую ВАХ можно
построить путем суммирования ординат вольт-амперных характеристик I = I1(U ) и
I = I2 (U ) элементов R1 и R2 при фиксированных значениях напряжения U .
Графическая интерпретация указанных построений приведена на рисунке 7.9, б.
Здесь для некоторого значения напряжения U = U a , задаваемого точкой « a » на оси
абсцисс, показано правило определения точки « d », принадлежащей результирующей
ВАХ I = I (U ) параллельного соединения сопротивлений R1 и R2 . Как следует из
рисунка, положение точки « d » при фиксированном значении напряжения определяется на основании графического уравнения



U = U a
ab + ac = ad , (7.10)


где отрезки ab и ac выражают в заданном масштабе m I
токи
I1a и
I2a
в элементах R1

и R2 , соответствующие выбранному значению напряжения U a , а отрезок ad — ток I a
в эквивалентном сопротивлении R при том же напряжении:

I1a = m I × ab ,

I2a = m I × ac ,

I a = m I × ad . (7.11)
Таким образом, графическое уравнение (7.10) соответствует 1-му закону
Кирхгофа I = I1 + I2 .
Для определения величины тока I при заданном по условию задачи значении
ЭДС E на оси напряжений откладывается точка « m¢», соответствующая в выбранном масштабе величине ЭДС E , из которой восстанавливается перпендикуляр до
пересечения с зависимостью I = I (U ) (на рисунке 7.9, б — это точка « m »). Из точки
пересечения перпендикуляра с кривой I = I (U ), т.е. из точки « m », опускается
ортогональ на ось токов — полученная точка « m¢ » соответствует искомому току
I = I (E ) в цепи. Ординаты точек пересечения перпендикуляра с зависимостями
I = I1(U ) и I = I2 (U ) определяют токи I1 и I2 в параллельных ветвях с
сопротивлениями
R1 и R2
(рисунок 7.9, б).
Примечание – Рассмотренный прием может быть обобщен на любое число нелинейных сопротивлений, соединенных параллельно.
7.5.3 Метод эквивалентных преобразований при смешанном соединении нелинейных сопротивлений
При смешанном соединении нелинейных резисторов, состоящем из последовательного и параллельного соединения отдельных участков цепи, для построения результирующей вольт-амперной характеристики всей цепи в целом могут быть использованы те же приемы. Расчет таких цепей производится в следующей последовательности:
1) исходная схема сводится к цепи с последовательным соединением сопротивлений, для чего строится результирующая ВАХ параллельного соединения так же, как это делалось в разделе 7.5.2;
2) производится расчет полученной схемы с последовательным соединением нелинейных сопротивлений (см. раздел 7.5.1), на основании которого затем определяются токи в параллельных ветвях схемы.
7.5.4 Метод пересечения характеристик
Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами (рисунок 7.10, а) может быть проведено другим методом — методом пересечения характеристик. В этом случае один из нелинейных резисторов,
например, R1 с ВАХ U = U1(I ) считается внутренним сопротивлением источника ЭДС
E , а другой ( R2 с ВАХ U = U 2 (I )) — нагрузкой.
 |  |
а) б)
Рисунок 7.10 – Последовательное соединение нелинейных сопротивлений (а) и графическая интерпретация метода пересечения характеристик (б)
Электрическое состояние цепи (рисунок 7.10, а) тогда определяется на основании
2-го закона Кирхгофа:
U2 (I ) = E -U1(I ). (7.12)
Графическое решение уравнения показано на рисунке 7.10, б. Это решение, как
видно из рисунка, определяется точкой пересечения кривой U (I ) = E - U1(I ) с вольт-
амперной характеристикой U 2 (I ) нелинейного сопротивления R2 , т.е. точкой « a », для
которой напряжение U2 (I ) на элементе R2 удовлетворяет уравнению (7.12).
Перпендикуляры, опущенные из точки пересечения « a » на оси координат,
определяют рабочий режим цепи, т.е. значения напряжений U1
и U2
на нелинейных
резисторах
R1 , R2
и величину тока I в последовательной цепи (рисунок 7.10, б).
Примечания
1 Кривая U (I ) = E - U1(I )
на рисунке 7.10, б строится путем вычитания ординат
ВАХ U1(I ) из ЭДС E для различных значений тока I .
2 Использование метода пересечения характеристик наиболее эффективно при последовательном соединении линейного и нелинейного сопротивлений (рисунок 7.11, а).
 |  |
а) б)
Рисунок 7.11 – Последовательное соединение линейного и нелинейного сопротивлений (а)
и графическая интерпретация метода пересечения характеристик (б)
В этом случае линейный резистор
R1 принимается за внутреннее сопротивление
источника ЭДС E , а электрическое состояние цепи определяет уравнение
U 2 (I ) = E - R1I1 , (7.13)
из которого следует, что кривая U (I ) = E - R1I1 может быть построена по двум точкам.
Обычно в качестве таких точек выбираются точки, соответствующие режимам холостого хода и короткого замыкания. Пример указанного построения демонстрирует
рисунок 7.11, б. Здесь ВАХ U (I ), соответствующая прямой MN , построена по двум
точкам M и N . Координаты точки M определяют режим холостого хода:
I = 0 ,
 U = E ; координаты точки N — режим короткого замыкания: I = I кз = E R1 ,
U = E ; координаты точки N — режим короткого замыкания: I = I кз = E R1 ,
U = 0 .
Как и в случае двух нелинейных резисторов, точка « a » пересечения кривых
U (I ) = E - R1I1 и U2 (I ), т.е. точка пересечения прямой MN и ВАХ U2 (I ) нелинейного
элемента
R2 , определяет режим цепи: напряжения U1, U 2
на элементах
R1 , R2
и силу
тока в цепи I (рисунок 7.11, б).
7.5.5 Метод эквивалентного генератора при расчете цепей постоянного тока с одним нелинейным элементом
Если в сложной электрической цепи имеется одна ветвь с нелинейным
резистором, то величину тока в ней можно определить методом эквивалентного генератора. Идея решения (как и в случае линейной цепи) заключается в следующем: ветвь, содержащую нелинейное сопротивление, выделяют из исходной схемы, а всю остальную (уже линейную) часть схемы рассматривают как активный двухполюсник (рисунок 7.12, а).
 |  |  |
а) б) в
Рисунок 7.12 – Замена активного двухполюсника (а) в нелинейной цепи эквивалентным источником напряжения (б) или эквивалентным источником тока (в)
Согласно теоремам об эквивалентных источниках (теореме Тевенена и теореме Нортона) активный двухполюсник по отношению к зажимам « a » и « b » выделенной ветви можно представить эквивалентным источником энергии (эквивалентным генератором). Как было показано в разделе 2.7.6, это можно сделать двумя способами — активный двухполюсник можно заменить эквивалентным источником напряжения с
 ЭДС E г
ЭДС E г
и внутренним сопротивлением
R г (рисунок 7.12, б) или эквивалентным
источником тока с задающим током J г
(рисунок 7.12, в).
и внутренней проводимостью
G г = 1 R г
ЭДС E г
эквивалентного источника напряжения равна согласно теореме Тевенена
напряжению
U хх
на зажимах « a » и « b » при разомкнутой ветви с нелинейным
сопротивлением (напряжению в режиме холостого хода), а внутренне сопротивление R г
совпадает с входным сопротивлением
R вх
двухполюсника:
E г = U хх , R г = R вх . (7.14)
Задающий ток J г
эквивалентного источника тока равен согласно теореме
Нортона току короткого замыкания
I кз
двухполюсника, а внутренняя проводимость G г
— входной проводимости двухполюсника G вх :
J г = I кз , G г = G вх . (7.15)
Определив параметры
E г , R г
или
J г , G г
эквивалентных источников в
соответствии с формулами (7.14), (7.15), ток I в выделенной ветви « ab », т.е. ток в нелинейном сопротивлении, можно рассчитать методом эквивалентных преобразований (как цепь с последовательным соединением элементов) или методом пересечения характеристик.
Примечание – Если по условию задачи необходимо также найти токи в линейной части исходной цепи, то после расчета нелинейной схемы нелинейный резистор на рисунке 7.12, б (или 7.12, в) в соответствие с принципом компенсации (см. раздел 2.9.3)
заменяется источником ЭДС или тока, после чего проводится анализ полученной линейной цепи любым методом расчета цепей постоянного тока.
7.5.6 Метод двух узлов при расчете цепей постоянного тока с нелинейными элементами
Для расчета цепей, содержащих два узла или сводящихся к таковым, можно применить метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем:
1) все токи I k
в параллельных ветвях схемы выражают в функции одного
переменного — напряжения U0
между двумя узлами, т.е. согласно формуле
U k = ±E ± U0 ; (7.16)
2) строят графики зависимостей I k (U0 ) токов во всех k - х ветвях в функции
общей величины — напряжения U0 . Для этого каждую из исходных кривых I k (U k )
смещают вдоль оси напряжений параллельно самой себе так, чтобы ее начало
находилось в точке U0 = E k . Если при этом напряжение U0
в формулу (7.16) входит со
знаком «–», то относительно перпендикуляра, восстановленного в точке
U0 = E k ,
производят зеркальное отражение вновь построенной кривой I k (U0 );
3)
 |
графически определяют точку, в которой реализуется 1-й закон Кирхгофа, т.е. уравнение
åI k (U0 ) = 0 . (7.17)
k =1
Рассмотрим практическую реализацию метода для схемы цепи, изображенной на рисунке 7.13, а.
 |  |
а) б)
Рисунок 7.13 – Схема нелинейной цепи с двумя узлами (а) и графическая интерпретация метода двух узлов (б)
Схема содержит три нелинейных элемента характеристики которых приведены на рисунке 7.14.
R1 , R2
и R3 , вольт-амперные
Выразим токи
I1 ,
I2 и I3
в ветвях схемы через узловое напряжение
U0 . Для
этого представим напряжения
U1, U 2
и U3
на нелинейных элементах как функции
соответствующих ЭДС
E1 ,
E2 , E3
и узлового напряжения U0 . В итоге получим:
U1 = E1 - U0 ,
U2 = E2 + U0 ,
U3 = E3 -U0 . (7.18)



Рисунок 7.14 – Вольт-амперные характеристики нелинейных сопротивлений
Графики кривых
I1(U0 ),
I2 (U0 ),
I3 (U0 ), построенные на основании
уравнений (7.18), изображены на рисунке 7.13, б. Согласно 1-му закону Кирхгофа для
токов
I1 ,
I2 , I3
в рассматриваемой цепи должно выполняться условие
I1(U0 )- I2 (U0 )+ I3 (U0 ) = 0 . (7.19)
Точку, в которой реализуется 1-й закон Кирхгофа (7.19), определяем графически,
как точку пересечения кривых (I1 + I3 ) с кривой I2 , т.е. согласно следующему из (7.19)
равенству:
I1(U0 )+ I3(U0 ) = I2 (U0 ).
На рисунке 7.13, б это точка « m ».
7.6 Аналитические методы расчета нелинейных цепей
Исследование общих свойств нелинейных цепей удобно осуществлять на основе математического анализа, базирующегося на аналитическом представлении характеристик нелинейного элемента, т.е. их аппроксимации. На выбор аналитического метода влияют условия поставленной задачи, а также характер возможного перемещения рабочей точки по характеристике нелинейного элемента: по всей характеристике или в ее относительно небольшой части.
К аналитическим методам относятся:
1) метод аналитической аппроксимации;
2) метод кусочно-линейной аппроксимации;
3) метод линеаризации.
7.6.1 Метод аналитической аппроксимации. Основные положения
Метод аналитической аппроксимации основан на замене вольт-амперной характеристики (или ее участка) нелинейного элемента общим аналитическим выражением.
Пусть ВАХ нелинейного сопротивления, соответствующая некоторой
функциональной зависимости y = f (x), где y = I , x = U или, наоборот, y = U , x = I ,
представлена в табличной форме (см. таблицу 7.1) или в виде точечной диаграммы
(рисунок 7.15). При этом вид самого аналитического выражения y = f (x) неизвестен.
Таблица 7.1 – Данные измерений при экспериментальном определении ВАХ нелинейного элемента
| x0 | x1 | x2 | x3 | K | x i | K | x n-1 | x n |
| y0 | y1 | y2 | y3 | K | y i | K | y n-1 | y n |

Рисунок 7.15 – Точечная диаграмма экспериментально снятой вольт-амперной характеристики нелинейного элемента
Важное практическое применение имеет следующая задача: найти аналитическое
выражение зависимости y = f (x) (вольт-амперной характеристики), т.е. подобрать
функци ю y = j(x) такую, чтобы y i = j(x i ) или y i » j(x i ). Функции, полученные в
результате решения такого рода задач, называются эмпирическими или
аппроксимирующими.
Подбор аппроксимирующей функции по экспериментальным значениям (x i ; y i ),
 i = 0,n , можно осуществить, исходя из различных моделей. Наиболее распространенными из них являются метод интерполирования и метод наименьших квадратов.
i = 0,n , можно осуществить, исходя из различных моделей. Наиболее распространенными из них являются метод интерполирования и метод наименьших квадратов.
7.6.2 Аналитическая аппроксимация по методу интерполирования
Интерполированием вольт-амперной характеристики y = f (x) нелинейного
 элемента, представленной таблицей значений (x i ; y i ), i = 0, n , называется
элемента, представленной таблицей значений (x i ; y i ), i = 0, n , называется
восстановление этой характеристики с заданной степенью точности эмпирической
функцией
y = j(x), удовлетворяющей условию
y i = j(x i ). Точки
x0 ,
x1 , K ,
x n-1 , x n
называют узлами интерполирования.
Геометрически задача подбора функции
j(x) по заданным частным значениям
ВАХ y = f (x) означает построение кривой y = j(x), проходящей через точки
 плоскости с координатами (x i ; y i ), i = 0, n , (рисунок 7.16).
плоскости с координатами (x i ; y i ), i = 0, n , (рисунок 7.16).
 |
Рисунок 7.16 – Геометрическая интерпретация метода интерполирования
Ясно, что через данные точки (x i ; y i ) можно провести бесконечное множество
различных кривых. Следовательно, задача подбора эмпирической функции
y = j(x) по
 данным значениям (узла м) (x i ; y i ), i = 0, n , неизвестной функции y = f (x) не определена.
данным значениям (узла м) (x i ; y i ), i = 0, n , неизвестной функции y = f (x) не определена.
Предположим теперь, что функция y = j(x) не произвольная, а является
многочленом степени n ( n — натуральное число, на единицу меньшее количества
узлов). Тогда задача подбора эмпирической функции j(x) приобретает более
определенный характер, так как функцию f (x) теперь требуется приближенно заменить многочленом
P n (x) = a n
x n + a
n-1
x n-1 +K+ a x +a
, (7.20)
|
|
 P n (x i ) = y i , i = 0, n . (7.21)
P n (x i ) = y i , i = 0, n . (7.21)
Многочлен P n (x) называется интерполяционным многочленом степени n . Для
определения коэффициентов a n , a n-1 , K , a1, a0 многочлена P n (x) используют условия (7.20), (7.21):
⎧a x n + a
x n-1 +K+ a x + a
= y ;
⎪ n 0
n-1 0
1 0 0 0
⎪a x n + a
x n-1 +K+ a x + a
= y ;
⎨ n 1
n-1 1
1 1 0 1
(7.22)
⎪.....................................................
|
|
|
|
|
|
|
|
|
В курсе высшей математики доказывается, что система уравнений (7.22) имеет
единственное решение, если узлы интерполирования
x0 ,
x1, K ,
x n-1 , x n
различны. Это
означает, что существует единственный интерполяционный многочлен коэффициенты которого определяются из системы (7.22).
P n (x),
При большом количестве узлов интерполирования определение коэффициентов
многочлена P n (x) на основании системы уравнений (7.22) связано с весьма
громоздкими вычислениями, поэтому на практике используют различные (специальные)
формы представления многочленов P n (x), наиболее распространенными из которых
являются интерполяционные многочлены Лагранжа и Ньютона.
|
( ) å
(x - x )(x - x ) K (x - x )(x - x ) K (x - x )
P n x =
y k ( 0 1
k -1
k +1
n . (7.23)
k =0
x k - x0 )(x k - x1 )K(x k - x k -1 )(x k - x k +1 )K(x k - x n )
Интерполяционным многочленом Ньютона называется многочлен
P n (x) = y0 + (x - x0 ) f (x0; x1 )+ (x - x0 )(x - x1 ) f (x0; x1; x2 )+K+
+ (x - x0 )(x - x1 )K(x - x n-1 ) f (x0; x1;K; x n ), (7.24)
где
f (x0; x1 ), f (x0; x1; x2 ), K , f (x0; x1;K; x n ) — разделенные разности:
|
; x ) =
y0 - y1 ,

f (x
; x ; x ) =
f (x0; x1 )-
f (x1; x2 ) , K ,
|
0 1 2

x0 - x2
f (x ; x ;K; x ) =
f (x0; x1;K; x n-1 )- f (x1; x2;K; x n ) . (7.25)

0 1 n
x0 - x n
Примечания
1 В силу единственности интерполяционного многочлена n - й степени
P n (x)
интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и наоборот.
2 На практике для получения достаточно хорошего приближения ВАХ y = f (x)
вместо построения интерполяционного многочлена высокой степени используют
кусочную интерполяцию многочленами более низких степеней, т.е. на каждом отрезке

|
|
на отрезке [x k ; x k +1] можно построить многочлен первой степени (кусочн о-линейная
интерполяция); при m = k + 2 на отрезке [x k ; x k +2 ] — многочлен второй степени
(кусочно-квадратичная интерполяция) и т.д. Получающиеся при этом кусочно-
|
|
(многочлены одной и той же степени) называются сплайн-функциями или просто сплайнами, а сам метод, основанный на представлении функции сплайнами — сплайн- интерполяцией. Простейший пример линейной сплайн-интерполяции некоторой
функции y = f (x), представляющей ВАХ нелинейного элемента, демонстрирует
рисунок 7.17.
 |
Рисунок 7.17 – Линейная сплайн-интерполяция вольт-амперной характеристики нелинейного элемента
7.6.3 Аналитическая аппроксимация по методу наименьших квадратов
 Пусть результаты измерения (x i ; y i ), i = 0, n , вольт-амперной характеристики
Пусть результаты измерения (x i ; y i ), i = 0, n , вольт-амперной характеристики
нелинейного элемента приведены в виде таблицы 7.1 или точечной диаграммы,
изображенной на рисунке 7.15. Значения ВАХ y = f (x) при x = x i определены приближенно с некоторой случайной погрешностью.
Наличие случайных погрешностей делает нецелесообразным подбор такой
эмпирической функции y = j(x), которая бы точно описывала все экспериментальные
 данны е, т.е. график ее проходил бы через точки (x i ; y i ), i = 0, n . В этом случае
данны е, т.е. график ее проходил бы через точки (x i ; y i ), i = 0, n . В этом случае
предпочтительно подобрать такую аппроксимирующую функцию j(x), которая
«сглаживала» бы случайные погрешности измерений.
Задача построения аппроксимирующей функции j(x) по экспериментальным
данным в рассматриваемой модели состоит из двух этапов:
1) определение вида аппроксимирующей функции
j(x), т.е. выбор класса
функций, к которому принадлежит аппроксимирующая функция (линейная,
квадратичная, показательная и т.д.);
2) определение параметров
j(x , b0 , b1 ,K, b m ) выбранного вида.
b0 , b1, K , b m
аппроксимирующей функции
Пусть далее первая часть задачи решена, т.е. вид аппроксимирующей функции
j(x , b0 , b1 ,K, b m ) определен. Подбор параметров b0 , b1, K , b m этой функции по
методу наименьших квадратов производится таким образом, чтобы сумма квадратов
отклонений экспериментальных значений была минимальной, т.е.
y i от ординат аппроксимирующей функции
|
S = [y - j(x ,b ,b ,Lb
k =0
)] 2= min . (7.26)
Задача определения тех значений параметров b0 , b1, K , b m , при которых
функция S (b0 , b1 ,Kb m ) достигает минимума, сводится к решению системы уравнений:
dS = 0 ,
db0
dS db1
= 0 , K ,dS = 0 . (7.27)
db m
Значения параметров
b0 , b1, K , b m
для функций наиболее часто используемых

 при аппроксимации ВАХ нелинейных элементов, систематизированы в таблице 7.2.
при аппроксимации ВАХ нелинейных элементов, систематизированы в таблице 7.2.
Таблица 7.2 – Параметры основных аппроксимирующих функций
| Вид аппроксимирующей функции | Параметры аппроксимирующей функции |
| j(x) = b1x + b0 | n n n åx iå y i - nåx i y i b1 = i= 1 i = 1 i = 1 , ⎛ n ⎞2 n ⎜åx i ⎟ - nåx i ⎜ ⎟ 2 ⎝ i=1 ⎠ i=1 1 ⎛ n n ⎞ b0 = n ⎜å y i - b1åx i ⎟ ⎜ ⎟ ⎝ i=1 i=1 ⎠ |
| j(x) = b2 x + b1x + b0 2 | ⎧ n n n ⎪ b2åx i + b1åx i + b0n =å y i ; 2 ⎪ i=1 i=1 i=1 ⎪ n n n n ⎨ b2åx i + b1åx i + b0åx i =åx i y i ; 3 2 ⎪ i=1 i=1 i=1 i=1 ⎪ n n n n ⎪ 2å i 1å i 0å i å i i ⎪b x4 + b x3 + b x2 = x2 y . ⎩ i=1 i=1 i=1 i=1 |
| j(x) = b0 x 1 b | ⎛ 1 ⎛ n n ⎞⎞ b0 = exp⎜ n ⎜åln y i - b1åln x i ⎟⎟ , ⎜ ⎜ ⎟⎟ ⎝ ⎝ i=1 i=1 ⎠⎠ |
Продолжение таблицы 7.2
| Вид аппроксимирующей функции | Параметры аппроксимирующей функции |
| n n n åln x iåln y i - nåln x i ln y i b1 = i= 1 i = 1 i = 1 ⎛ n ⎞2 n ⎜åln x i ⎟ - nå(ln x i ) 2 ⎜ ⎟ ⎝ i=1 ⎠ i=1 | |
| j(x) = b0 exp(b1x) | ⎛ 1 n n ⎞ b0 = exp⎜ n åln y i - b1åx i ⎟ , ⎜ ⎟ ⎝ i=1 i=1 ⎠ n n n åx iåln y i - nåx i ln y i b1 = i= 1 i = 1 i = 1 ⎛ n ⎞2 n ⎜åx i ⎟ - nåx i ⎜ ⎟ 2 ⎝ i=1 ⎠ i=1 |
| j(x) = b0 + b1 x | 1 ⎛ n n 1 ⎞ b0 = n ⎜å y i - b1å x ⎟ , ⎜ ⎟ ⎝ i=1 i=1 i ⎠ n n n nå(y i x i )-å(1 x i )å y i b1 = i= 1 i = 1 i = 1 ån ⎛ån ⎞2 n (1 x i )- ⎜ (1 x i )⎟ 2 ⎜ ⎟ i=1 ⎝ i=1 ⎠ |
| j(x) = b0 + b1 ln x | 1 ⎛ n n ⎞ b0 = n ⎜å y i - b1åln x i ⎟ , ⎜ ⎟ ⎝ i=1 i=1 ⎠ n n n nå(y i ln x i )-å y iåln x i b1 = i= 1 i = 1 i = 1 n ⎛ n ⎞2 nå(ln x i ) - ⎜åln x i ⎟ 2 ⎜ ⎟ i=1 ⎝ i=1 ⎠ |
Примечание – При подборе аппроксимирующей функции y = j(x)
следует
учитывать характер расположения экспериментальных точек (x i ; y i ),

i = 0,n на








 точечной диаграмме и сочетать его по возможности с логически-профессиональным анализом.
точечной диаграмме и сочетать его по возможности с логически-профессиональным анализом.
7.6.4 Метод кусочно-линейной аппроксимации
Метод кусочно-линейной аппроксимации основан на представлении ВАХ нелинейного элемента отрезками прямых линий по аналогии с линейной сплайн-
интерполяцией, изображенной на рисунке 7.17. В результате нелинейная цепь может быть описана линейными уравнениями с постоянными (в пределах каждого отрезка) коэффициентами.
7.6.5 Метод линеаризации
Метод линеаризации применим для анализа нелинейных цепей при малых отклонениях рабочей точки « a » (рисунок 7.18) от исходного состояния, а также в случаях, когда ВАХ нелинейного элемента в пределах некоторого диапазона изменения тока или напряжения содержит линейный участок.
 |  |
а) б)
Рисунок 7.18 – Вольт-амперные характеристики нелинейных элементов с восходящим (а)
и нисходящим (б) участками
В этих случаях можно осуществить замену данного нелинейного элемента
эквивалентной линейной схемой, состоящей из источника ЭДС
E0 и линейного
сопротивления R д
или источника тока
J0 и линейной проводимости
G д . Линейное
сопротивление R д
в таком случае соответствует дифференциальному сопротивлению
нелинейного резистора, а линейная проводимость G д
проводимости:
— его дифференциальной
R = dU
д dI
» ÄU ,
Ä I
G = dI»
д dU
ÄI . (7.28)
Ä U
Пусть, например, рабочая точка « a » расположена на восходящей части ВАХ (рисунок 7.18, а). В пределах линейного участка « ab » характеристики напряжение U0 на нелинейном элементе может быть представлено уравнением
U0 = E0 + R д I . (7.29)
Этому уравнению соответствует схема замещения нелинейного элемента, изображенная на рисунке 7.19, а (схема замещения с источником ЭДС).
Разделив почленно уравнение (7.29) на величину R д
и преобразовав полученное
выражение относительно тока I , получим новое уравнение:
I = -J0 + U0G д = -J0 + I д , (7.30)

 где G д = 1 R д ,
где G д = 1 R д ,
J0 = E0
R д ,
I д = U0G д .
Уравнению (7.30) соответствует схема замещения нелинейного элемента, изображенная на рисунке 7.19, б (схема замещения с источником тока).


а) б)
Рисунок 7.19 – Схемы замещения нелинейного элемента на восходящей части его вольт-амперной характеристик, содержащие источник ЭДС (а)
и источник тока (б)
Пусть теперь рабочая точка « a » расположена на нисходящей части ВАХ (рисунок 7.18, б). В пределах линейного участка « ab » характеристики напряжение U0 на нелинейном элементе может быть представлено уравнением
U0 = -E0 + R д I . (7.31)
Этому уравнению соответствует схема замещения нелинейного элемента, изображенная на рисунке 7.20, а (схема замещения с источником ЭДС).
 |  |
а) б)
Рисунок 7.20 – Схемы замещения нелинейного элемента на нисходящей части его вольт-амперной характеристик, содержащие источник ЭДС (а)
и источник тока (б)
Разделив почленно уравнение (7.31) на величину R д
и преобразовав полученное
выражение относительно тока I , получим новое уравнение:
I = J0 + U0G д = J0 + I д . (7.32)
Уравнению (7.32) соответствует схема замещения нелинейного элемента, изображенная на рисунке 7.20, б (схема замещения с источником тока).
7.6.6 Закон Ома и законы Кирхгофа для малых приращений
На основании метода линеаризации могут быть получены законы Ома и Кирхгофа для малых приращений. Как было показано в разделе 7.6.5, при незначительном отклонении рабочей точки от исходного состояния, дифференциальное сопротивление (или дифференциальную проводимость) нелинейного резистора с достаточной точностью можно определить как отношение приращений тока и напряжения, т.е. в соответствии с формулами (7.28). Из этих формул тогда получаем:
Ä I = ÄU ,
R д
Ä I = G д Ä U . (7.33)
Соотношения (7.33) называются законами Ома для малых приращений.
Если в результате расчета нелинейной цепи исходный режим ее уже определен и требуется рассчитать лишь приращения токов или напряжений, обусловленные
изменением напряжения или тока источника, целесообразно использовать для расчетов эквивалентные схемы для приращений. Эти схемы могут быть получены из соответствующих законов Кирхгофа для приращений.
|
|

= å Ä I k ,
k =1
å Ä I k k =1
= 0 . (7.34)
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма приращений падений напряжения на сопротивлениях контура равна алгебраической сумме приращений ЭДС, действующих в контуре:
|

= åÄ E k . (7.38)
k =1
При составлении схемы замещения для приращений следует придерживаться двух следующих правил:
1) все ЭДС и токи источников, т.е. величины E и J , заменить их приращениями
E и Ä J ;
2) нелинейные резисторы заменить линейными сопротивлениями (или
проводимостями), равными дифференциальным в рабочих точках.
Примечание – Необходимо помнить, что величина какого-либо тока или напряжения в цепи равна алгебраической сумме ее исходного значения и приращения, рассчитанного методом линеаризации, т.е. согласно законам Ома и Кирхгофа для малых приращений. Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости.
7.7 Численные методы расчета нелинейных цепей
Решение нелинейного уравнения (или системы уравнений), описывающего состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня, после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.
Наиболее широкое применение в теоретической электротехнике для расчета нелинейных резистивных цепей получили метод простых итераций (метод последовательных приближений) и метод Ньютона (метод касательных).
7.7.1 Метод простых итераций
В наиболее компактной форме метод простых итераций применяется к решению уравнений вида
x = f (x), (7.39)
где величина x представляет искомый ток или напряжение, т.е.
x = I
или
x = U .
Для уравнения (7.39) тогда имеем следующий итерационный процесс:
x k +1 =
f (x k ),

k = 0,n , (7.40)
где x k и x k +1 — значения искомой величины x на k - м и (k + 1)- м шаге итераций;
*
f (x k ) — значение функции f (x) на k - м шаге итерации.
Геометрическую интерпретацию метода можно представить, изобразив на
координатной плоскости графики функций y = f (x) и y = x . Абсцисса точки
пересечения графиков этих функций (точка (рисунок 7.21).
x * ) и есть решение уравнения (7.39)

Рисунок 7.21 – Геометрическая интерпретация метода простых итераций
Значение
x0 на рисунке 7.21 обозначает первоначальное приближение к корню x
|
завершить при достижении на очередном шаге итерации значения
x k +1 , которое
отличается от предыдущего значения x k
на величину
 x k +1 - x k
x k +1 - x k
£ e , (7.41)
 где — заданная заранее погрешность вычислений.
где — заданная заранее погрешность вычислений.
Примечание – Начальное приближение
x0 для итерационного процесса (7.40)
обычно находится из уравнения f (x)- x = 0
членами.
при пренебрежении в нем нелинейными
в виде
7.7.2 Метод Ньютона
Суть этого метода заключается в следующем. Пусть нелинейное уравнение задано
f (x) = 0 . (7.42)
Допустим, что два приближенных значения x k
и x k +1
отличаются на малую
величину Ä x = x k +1 - x k . Тогда, разложив функцию f (x k + Ä x) в ряд по Ä x и
ограничившись только двумя первыми членами ряда (что справедливо, если Ä x —
малая величина), получим
f (x k + Ä x) » f (x k )+ f ¢(x k )Ä x . (7.43)
Целесообразно выбрать Ä x таким, чтобы f (x k + Ä x) = 0 . Тогда из (7.43) следует
Ä x = x
- x = -
f (x k )

или
k +1 k
f ¢(x k )
|
- f (x k ) ,

 |
k = 0,n . (7.44)
k +1
k f ¢(x )
Соотношение (7.44) также определяет некоторый итерационный процесс решения нелинейного уравнения (7.42). Этот процесс называется методом Ньютона. Геометрическая интерпретация метода приведена на рисунке 7.22.

Рисунок 7.22 – Геометрическая интерпретация метода Ньютона
В методе Ньютона также следует задать некоторое начальное приближение Итерационный процесс (7.44) следует завершить по достижении условия (7.41).
Примечания
x0 .
1 Начальное приближение x0 в методе Ньютона находится по тому же принципу,
что и в методе простых итераций, т.е. на основании уравнения пренебрежении в нем нелинейными членами.
f (x) = 0
при
2 На интервале между точками x k и x k +1 , являющимися приближенными
значениями корня
x * уравнения (7.42), должны выполняться следующие условия:
df (x) ¹ 0 ,
dx
d 2 f (x)

dx2
¹ 0 , (7.45)
так как в противном случае итерационный процесс (7.44) будет расходящимся.
Дата добавления: 2019-07-15; просмотров: 393; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
