Лекция 6. Переходные процессы в линейных электрических цепях и методы их анализа 11 страница

⇐ ПредыдущаяСтр 27 из 35Следующая ⇒

входная величина f (t ) = 1(t ), то выходной величиной будет h(t ) = x(t ).

Рисунок 6.23 – Диаграмма, поясняющая смысл переходной характеристики

Поскольку воздействие начинается в момент времени

t = 0 , то отклик

h(t ) = 0

при t < 0 , поэтому более строгая математическая запись переходной характеристики

имеет вид

h(t )×1(t ).

Если воздействие на цепь (например, напряжение) происходит не только в момент

включения t = 0 , а и дополнительными порциями с запаздыванием на некоторое время

t1 , t 2 , K , t k , то и переходная характеристика также может быть представлена с запаздывающим аргументом, т.е.

или

h(t -t1 ), h(t -t 2 ), K , h(t -t k )

h(t -t1 )×1(t -t1 ), h(t -t 2 )×1(t -t 2 ), K , h(t -t k )×1(t -t k ).

Переходная характеристика h(t ) имеет несколько разновидностей, представленных в таблице 6.6.

Таблица 6.6 – Переходные характеристики цепи

Вид воздействия f (t )	Вид реакции x(t )	Переходная характеристика h(t )
Единичный скачок тока	Ток	k i (t ) — коэффициент передачи по току
Единичный скачок тока	Напряжение	z(t ) — переходное сопротивление

Продолжение таблицы 6.6

Вид воздействия f (t )	Вид реакции x(t )	Переходная характеристика h(t )
Единичный скачок напряжения	Ток	y(t ) — переходная проводимость
Единичный скачок напряжения	Напряжение	k u (t ) — коэффициент передачи по напряжению

Примечание – Существует два способа определения переходной характеристики

— расчетный и экспериментальный.

Для определения переходной характеристики расчетным способом необходимо: классическим методом определить отклик цепи на постоянное воздействие; полученный отклик разделить на величину постоянного воздействия и тем самым определить переходную характеристику.

При экспериментальном определении переходной характеристики необходимо: на вход цепи подать постоянное напряжение и снять осциллограмму реакции цепи; полученные значения пронормировать относительно входного напряжения — это и есть переходная характеристика.

В качестве примера определим переходную характеристику R , C – цепи, изображенной на рисунке 6.6, а. В разделе 6.8.1 было установлено, что реакция данной цепи (сила тока) на постоянное воздействие (постоянную ЭДС E ) определяется выражением (6.39):

( ) E - t

i t = e t ,

= RC .

Разделив силу тока

R , C – цепи по току:

i(t ) на величину ЭДС E , получим переходную характеристику

( ) i(t ) ( ) 1

- t( )

h i t =

×1 t

= e t ×1 t R

. (6.151)

6.20.2 Импульсная характеристика цепи

Импульсная характеристика g(t ) электрической цепи (функция веса) — это

отклик (реакция) цепи на дельта-функцию при нулевых начальных условиях

(рисунок 6.24), т.е. если входная величина

g(t ) = x(t ).

f (t ) = d (t ), то выходной величиной будет

Рисунок 6.24 – Диаграмма, поясняющая смысл импульсной характеристики

Поскольку воздействие начинается в момент времени

t = 0 , то отклик

g(t ) = 0

при t < 0 , поэтому более строгая математическая запись переходной характеристики

имеет вид

g(t )×1(t ).

Если воздействие на цепь (например, напряжение) происходит не только в момент

включения t = 0 , а и дополнительными порциями с запаздыванием на некоторое время

t1 , t 2 , K , t k , то и импульсная характеристика также может быть представлена с запаздывающим аргументом, т.е.

или

g(t -t1 ), g(t -t 2 ), K , g(t -t k )

g(t -t1 )×1(t -t1 ), g(t -t 2 )×1(t -t 2 ), K ,

g(t -t k )×1(t -t k ).

Так как дельта-функция является первой производной от единичной функции и рассматриваемая электрическая цепь линейная, то аналогичная связь существует и

между импульсной и переходной характеристиками g(t ) и h(t ):

g(t ) = dh(t ) = h¢(t ), (6.152)

т.е. импульсная характеристика равна первой производной от переходной характеристики. Из (6.152) следует и обратное соотношение

h(t ) =ò g(t )d t . (6.153)

Используя правила дифференцирования произведения функций, соотношение (6.152) можно преобразовать к виду

g(t ) = (h(t )×1(t ))¢ = h¢(t )×1(t )+ h(t )d (t )

или при нулевых начальных условиях

(6.154)

g(t ) = (h(t )×1(t ))¢ = h¢(t )×1(t )+ h(0)d (t ). (6.155)

Примечание – Существует два способа определения импульсной характеристики

— расчетный и экспериментальный.

Расчетным способом импульсную характеристику определяют по переходной характеристике на основании формул (6.154) или (6.155).

При экспериментальном определении импульсной характеристики необходимо:

на вход цепи подать, например, прямоугольный импульс длительностью t и << t и снять

осциллограмму реакции цепи; полученные значения пронормировать относительно площади входного процесса — это и есть импульсная характеристика.

В качестве примера определим импульсную характеристику R , C – цепи, изображенной на рисунке 6.6, а. В разделе 6.20.1 было получено соотношение (6.151)

для переходной характеристики этой цепи. Импульсная характеристика в соответствии с выражением (6.155) тогда будет иметь вид

⎞

⎛ 1 - t ¢

1 - 0

1 - t 1

g i (t ) = ⎜ e t ⎟

⎝ R ⎠

×1(t )+ e R

t d (t ) = - e t

R t

+ d (t ).

6.21 Определение реакции цепи на воздействие произвольной формы. Формула интеграла Дюамеля

Пусть требуется определить ток i(t ) в линейном пассивном двухполюснике,

переходная характеристика h(t ) которого известна, при включении двухполюсника на

напряжение u(t ), т.е. внешнее воздействие f (t ) на цепь представлено напряжением, а

реакция (отклик) цепи на это воздействие — силой тока: напряжения u(t ) изображена на рисунке 6.25.

f (t ) = u(t ),

x(t ) = i(t ). Кривая

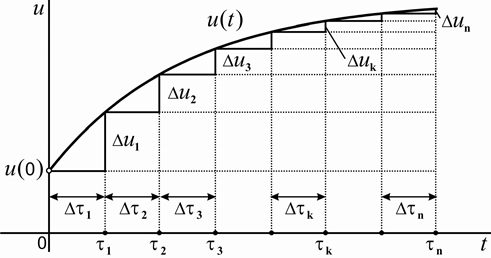
Рисунок 6.25 – Кривая напряжения на входе пассивного двухполюсника и ее представление совокупностью элементарных скачков

Выберем некоторый произвольный фиксированный момент времени t и рассчитаем переходной ток к этому моменту времени. В связи с этим введем новое

обозначение текущего времени через , изменяющегося в пределах 0 £ t £ t .

В дальнейшем будем различать u(t ) и i(t ) как функции момента наблюдения t , а

u(t ) и i(t ) — как функции текущего времени .

Заданное непрерывно изменяющееся напряжении u(t ) приближенно представим в

виде суммы начального напряжения u(0), включаемого в момент времени t = 0 , и

большого числа последовательно включаемых элементарных скачков напряжения

Ä u1 , Ä u2 , K , Ä u k , K , Ä u n , каждый из которых после включения действует от

момента времени t k ( k = 1,n ) до бесконечности (рисунок 6.25).

Под влиянием скачка напряжения

u(0) в цепи возникает переходной процесс. До

момента наблюдения переходной процесс будет продолжаться t секунд.

Под влиянием скачка напряжения Ä u1 , включаемого в момент времени

t1 , в

соответствии с принципом наложения возникнет дополнительный переходной процесс, продолжительность которого к моменту наблюдения t составит (t -t1 ) секунд.

Продолжая рассуждения аналогичным образом, придем к выводу, что продолжительность переходного процесса, возникающего в цепи под влиянием скачка

Ä u k , до момента наблюдения t будет (t -t k ) секунд и т.д.

Используя единичную функцию с запаздывающим аргументом, можно приложенное к цепи напряжение u(t ) приближенно записать в виде суммы

u(t ) » u(0)1(t )+ Ä u11(t -t1 )+ Ä u21(t -t 2 )+K+ Ä u k1(t -t k )+K+ Ä u n1(t -t n )

или

u(t ) » u(0)1(t )+åÄ u k1(t -t k ). (6.156)

k =1

Реакция цепи (в рассматриваемом случае — ток) определится как алгебраическая

сумма реакций цепи на воздействие начального напряжения

u(0)

и всех последующих

скачков напряжения

Ä u k , включаемых друг за другом.

Под влиянием составляющей напряжения u(0)1(t ) в цепи появится составляющая

тока i(t ), которая к моменту наблюдения t приобретет значение i(t ) = u(0)h(t ).

Спустя время t1 напряжение возрастет скачком на величину Ä u1 , что вызовет

ответную реакцию цепи в виде добавочной составляющей тока Ä i1 = Ä u1h(t -t1 ).

Продолжая рассуждения аналогичным образом, найдем, что в момент t k

скачок

напряжения Ä u k вызовет ток Ä i k = Ä u k h(t -t k ) и т.д.

Искомый переходной ток будет равен сумме составляющих, найденных для момента времени t , т.е.

i(t ) » u(0)h(t )+ Ä u1h(t -t1 )+ Ä u2h(t -t 2 )+K+ Ä u k h(t -t k )+K+ Ä u n h(t -t n )

или

i(t ) » u(0)h(t )+åÄ u k h(t -t k ), (6.157)

k =1

где n — число промежутков, на которые разбит интервал времени от 0 до t .

Чтобы получить выражение для тока, соответствующего не ступенчатому, а

непрерывному напряжению, необходимо промежутки (скачки) времени Ät k уменьшить

до бесконечно малой величины d t , а число промежутков увеличить до

бесконечности ( n ® ¥ ). В этом случае сами скачки будут величинами бесконечно

малыми, т.е. lim Ä u k = du k = u k¢ (t )d t , Ä t ® d t , n ® ¥ , а сумма в выражении (6.157)

перейдет в интеграл. Следовательно, ток напряжение u(t ) будет равен:

i(t )

в цепи как отклик на непрерывное

i(t ) = u(0)h(t )+òu¢(t )h(t -t )d t , (6.158)

где u¢(t ) — производная напряжения в точке t = .

Уравнение (6.158) и его частные виды называют формулой интеграла Дюамеля или просто интегралом Дюамеля. Соотношение (6.158) есть первая форма интеграла Дюамеля. Для расчета тока по формуле (6.158) необходимо знать закон изменения

заданного напряжения u(t ) в аналитической форме и переходную характеристику цепи

h(t ). Напряжение, подводимое к цепи, задается, а переходная характеристика, как

отмечалось выше, определяется из расчета переходного процесса в цепи при воздействии на нее единичного скачка напряжения.

Из теории определенных интегралов известно, что для любых двух функций и f2 (t ) существует соотношение

f1(t )

ò f1(t -t ) f2 (t )d t

=ò f1(t ) f2 (t -t )d t , (6.159)

которое является интегралом свертки. Это соотношение легко проверить путем замены переменных интегрирования.

Для получения второй формы интеграла Дюамеля воспользуемся свойством коммутативности свертки (6.159). Тогда

i(t ) = u(0)h(t )+òu¢(t -t )h(t )d t . (6.160)

Используя правило интегрирования по частям в первой форме записи интеграла Дюамеля (6.158), найдем третью форму записи:

i(t ) = u(0)h(t )+òu¢(t )h(t -t )d t

= u(0)h(t )+òh(t -t )du(t ) =

= u(0)h(t )+ u(t )h(t -t )t

+òu(t )h¢(t -t )d t .

Подставив пределы интегрирования, получим

i(t ) = u(t )h(0)+ òu(t )h¢(t -t )d t . (6.161)

Согласно свойству коммутативности свертки (6.159) выражении (6.161) можно записать так:

i(t ) = u(t )h(0)+ òu(t -t )h¢(t )d t . (6.162)

Уравнение (6.162) является четвертой формой интеграла Дюамеля. Пользуясь правилом дифференцирования определенных интегралов по параметру, все четыре формы записи интеграла Дюамеля (6.158), (6.160) – (6.162) можно свести к двум:

i(t ) =d u(t )h(t -t )d t ,

i(t ) =d u(t -t )h(t )d t . (6.163)

Соотношения (6.163) называют соответственно пятой и шестой формами интеграла Дюамеля.

Дата добавления: 2019-07-15; просмотров: 189; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 22 23 24 25 262728 29 30 31 Следующая ⇒

Мы поможем в написании ваших работ!