Лекция 6. Переходные процессы в линейных электрических цепях и методы их анализа 10 страница

B n¢ (p k )

Соотношение (6.137) называется формулой разложения. Величины  B n¢ ( p k ) в этой

формуле есть значения производных многочлена B n ( p) при p = p k , т.е. числа

B n¢ ( p k  ) =

.

p= p k

Основная  трудность  применения  теоремы  разложения,  т.е.  формулы  (6.137),

заключается в необходимости определения корней алгебраического                      уравнения

степени n B n ( p) = 0 . При степени n > 4 , а практически и при n > 2 корни многочлена

B n  ( p) могут быть определены только численно. Такая же трудность встречается и в

классическом методе при определении корней характеристического уравнения (6.10).

Остановимся на некоторых вспомогательных приемах, позволяющих найти оригинал по изображению функции, которое не удовлетворяет требованиям теоремы разложения.

1.

n

m

k

Если один из корней многочлена разложения (6.137) принимает иной вид:

B n  ( p), допустим

p1, равен нулю, то формула

f

t

=

m

+

( )  A ( 0 ) å

 A ( p )

B n¢ (0)

 

e p k t  .                                            (6.138)

k =2

B n¢ ( p k  )

Многочлен

B n  ( p)

может иметь корень в начале координат ( p1 = 0 ), когда в

данной цепи действуют источники постоянной ЭДС или постоянного тока. Выделенный постоянный член в формуле (6.138) представляет собой установившийся ток или напряжение в цепи.

2. Если B n  ( p) имеет пару сопряженных чисто мнимых  корней p1 = j w  и

p2 = - j w , то формулу разложения (6.137) можно записать так:

f

t

=

m

( )  A ( jw )

 A ( - jw )

å A ( p )

e j w t +

m

B n¢ ( j w )

B n¢ (-

j w )

 

n

e- j w t +

m

k

e p k t .                       (6.139)

k =3

B n¢ ( p k  )

Многочлен

B n  ( p)

может иметь пару чисто мнимых сопряженных корней в

случае, если рассматривается переходной процесс при наличии в цепи источников синусоидальных ЭДС или источников синусоидальных токов. Два первых выделенных члена в формуле (6.139) определяют синусоидальный ток или напряжение установившегося режима.

3. Если многочлен B n ( p) наряду с простыми корнями p1, p2 , K , p s ( s < n ),

имеет, например, еще один  - кратный корень p n , т.е. B n  ( p) = C s  ( p)( p - p n ) , где

a

— целое положительное число, то формула разложения (6.137) определяется равенством

s

A (p

)e p k t

1 d a -1

⎡ A ( p) ⎤

[

f (t ) =å   m k

 

⎢      e ⎥

 m   pt

+

a -1

.   (6.140)

k =1

d C

dp s

( p)( p - p n

)a ]

 

p= p k

(a -1)! dp

⎣ C s (p)

⎦ p= p

n

Если кратных корней несколько и каждый имеет свою кратность, то для каждого из них нужно записать слагаемое, аналогичное второму члену в правой части равенства (6.140).

 

6.18 Расчет переходных процессов методом интеграла Дюамеля. Основные положения

Метод интеграла Дюамеля (метод наложения) основан на принципе наложения, который позволяет искать общее решение линейных уравнений как линейную комбинацию, т.е. наложение более простых решений.

Идея подхода к анализу переходных процессов методом наложения следующая.

Допустим, что  внешнее  воздействие f (t ) можно представить совокупностью более

простых, аналитически однотипных функций f k (t ), т.е.

¥

 

 

Если искать реакцию

f (t ) =å f k (t ). k =1

x k (t ) исследуемой линейной цепи на воздействие

 

f k (t ), то

на основании принципа наложения можно утверждать, что реакция цепи

x(t ) на

заданное воздействие f (t ) равна сумме реакций x k (t ), т.е.

¥

x(t ) =åx k (t ).

k =1

Следовательно, расчет переходного процесса в линейной цепи методом интеграла Дюамеля состоит из двух основных этапов:

1) определение реакции цепи x k (t ) на заданное простое воздействие f k  (t );

2) суммирование (наложение) частных решений x k (t ) и определение реакции

цепи на исходное (сложное) воздействие f (t ).

Вид функции x k (t ) при заданном элементарном воздействии

f k (t ) зависит только

от схемы цепи и параметров электрической цепи.

Элементарные составляющие f k (t ) внешнего воздействия

f (t ) целесообразно

выбирать так, чтобы они были математически простыми, и расчет реакций вызываемых, был бы несложен.

x k (t ), ими

 

6.19 Типовые функции воздействия

При исследовании динамических свойств линейных цепей в качестве типовых

элементарных воздействий используются единичная ступенчатая функция дельта-функция (импульсная функция) d (t ).

6.19.1 Единичная функция воздействия

1(t ) и

Единичная функция воздействия

1(t ), называемая также функций Хевисайда

(рисунок 6.19, а), имеет следующие значения:

⎨1

1(t ) = ⎧0

⎩

при

При

t < 0;

t > 0

(6.141)

и обычно не определена при t = 0 .

а)                                                 б)                                                в)

Рисунок 6.19 – Единичная функция воздействия в стандартной форме (а),

с запаздывающим (б) и опережающим (в) аргументом

Единичная функция может быть с запаздыванием 1(t -t ) (рисунок 6.19, б) или с

опережением 1(t + t ) (рисунок 6.19, в):

⎨

1(t -t ) = ⎧0

⎩1

При при

t < t ;

t > t ,

1(t +t ) = ⎧0

⎨1

⎩

При при

t < -t ;

t > -t .

 

(6.142)

В теории цепей единичная функция, например, соответствует включению

постоянного напряжения на вход устройства при замыкании ключа. Если к цепи  в

момент времени t = t0 подключается напряжение u(t ), это соответствует воздействию

вида f (t ) = u(t )1(t - t0 ), т.е. единичная функция обладает важным формирующим

свойством: при умножении непрерывной функции на единичную получается разрывная функция (рисунок 6.20).

Рисунок 6.20 – Разрывная функция               Рисунок 6.21 – Прямоугольный импульс

Прямоугольный импульс (рисунок 6.21) с помощью единичной функции можно представить разностью

f (t ) = U m [1(t - t1 )-1(t - t2 )],

где U m — амплитуда импульса.

При умножении единичной функции на постоянное число получается ступенчатая функции, которую называют функцией включения:

⎨A

A ×1(t ) = ⎧ 0

⎩

При при

t < 0;

t > 0.

 

6.19.2 Импульсная функция воздействия

Импульсная функция воздействия d (t ), называемая также дельта-функцией или

функцией Дирака, относится к классу особых функций и представляет собой удобную математическую модель таких быстро протекающих процессов как включение и выключение электрического напряжения, короткое замыкание и обрыв в электрической цепи, воздействие на электрическую цепь кратковременных импульсов. Результат таких воздействий  часто  не  зависит  от  формы  импульса,  а  определяется  интегральным

значением, т.е. площадью импульса.

Наиболее просто к понятию дельта-функции d (t ) можно прийти на основе

выражения для прямоугольного импульса (рисунок 6.22).

На рисунке 6.22 прямоугольный импульс, определяемый функцией

d (t , Ä t ),

выбран так, чтобы его высота A и длительность Ä t

соотношениях:

находились в следующих числовых

=

1

A Ä t ,

S = A Ä t = 1,

где S — площадь импульса. При таких соотношениях с уменьшением длительности

импульса Ä t его высота A увеличивается, а площадь S остается неизменной и равной

единице: S = 1 = const .

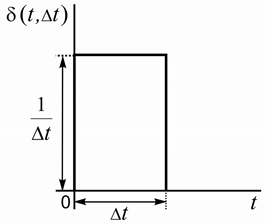
Рисунок 6.22 – График функции, определяющей прямоугольный импульс

Функцию d (t , Ä t ) можно представить аналитическим выражением

⎨A

d (t , Ä t ) = ⎧0

⎩

При при

t < 0 и t > Ä t; 0 < t < Ä t

 

(6.143)

или с помощью единичных функций по формуле

d (t , Ä t ) = 1 (t ) - 1 (t -  Ät ) .                                                                                       (6.144)

Ä t

Предельный случай прямоугольного импульса (6.143) или (6.144), когда его

длительность стремится к нулю ( Ä t ® 0 ), а высота импульса                        стремится к

бесконечности  ( A ® ¥ ),  называется  импульсной  функцией  воздействия d (t )                                                                                           или

дельта-функцией Дирака:

d (t ) = lim d (t , Ä t ) = lim 1 (t ) - 1 (t -  Ät ) .                                                                                                    (6.145)

Ä t®0

Ä t®0         Ä t

Для дельта-функции справедливы соотношения:

+¥

d (t ) = 0

( t ¹ 0 ),

d (0) = ¥ ,

òd (t )dt = 1.                        (6.146)

-¥

При смещении дельта-функции вправо по оси абсцисс на время получим

+¥

d (t -t ) = 0

( t ¹ ),

òd (t -t )d t

-¥

= 1.                            (6.147)

Важным  свойством дельта-функции  является возможность                 выделять

(отфильтровывать) с ее помощью значения заданной функции f (t ) в произвольный

момент времени t = :

+¥                                          +¥

ò f (t )d (t -t )d t =

-¥

f (t ),

ò f (t -t )d (t )d t =

-¥

f (t )

(6.148)

в частности, в нулевой момент времени, т.е. при t = 0

+¥

ò f (t )d (t )dt =

-¥

f (0).

Примечание – Между импульсной и единичной функциями существует аналитическая связь, которую можно установить на основании формулы (6.145). Указанный в этой формуле предельный переход соответствует производной, следовательно,

d (t ) = d1 (t ) = 1¢(t ),                                                                                  (6.149)

dt

т.е. дельта-функция равна первой производной от единичной функции. Из (6.149)

следует и обратное соотношение

t

1(t ) = òd (t )d t .                                                                                (6.150)

-¥

 

6.20 Временные характеристики электрических цепей

Временной характеристикой электрической цепи называется отклик цепи на типовое воздействие при нулевых начальных условиях. Временными характеристиками

электрической цепи являются переходная h(t ) и импульсная g(t ) характеристики.

 

6.20.1 Переходная характеристика цепи

Переходная характеристика h(t ) электрической цепи — это отклик (реакция)

цепи на единичную функцию при нулевых начальных условиях (рисунок 6.23), т.е. если

---

Дата добавления: 2019-07-15; просмотров: 167; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!