Тема 3. Дифференциальное исчисление функций одной переменной
Лекция 10-11. Производная функции.
Основные вопросы:
- Задачи, приводящие к понятию производной.
- Определение производной, ее геометрический, механический и экономический смысл. Связь между непрерывностью и дифференцируемостью функции.
- Правила и формулы дифференцирования.
Обзор лекции:
В данной лекции рассматриваются задачи, приводящие к понятию производной, понятие производной функции, геометрический, механический и экономический смысл производной, правила и методы дифференцирования функций.
1. Задачи, приводящие к понятию производной.
Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s(t), где t— время (в секундах), s(t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
Решение . Предположим, что в момент времени t тело находилось в точке M.
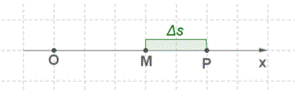
Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент времени t+Δt. Координата материальной точки станет другой, тело в этот момент будет находиться в точке P:OP=s(t+Δt).
Значит, за Δt секунд тело переместилось из точки M в точку P. Имеем: MP=OP−OM=s(t+Δt)−s(t). Полученную разность мы назвали в приращением функции: s(t+Δt)−s(t)=Δs.
|
|
|
Итак, MP=Δs(м). Нетрудно найти среднюю скорость vср движения тела за промежуток времени [t;t+Δt]: vср=ΔsΔt (м/с).
А что такое скорость v(t) в момент времени t (ее называют мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени [t;t+Δt] при условии, что Δt выбирается все меньше и меньше; точнее: при условии, что Δt→0. Это значит, что v(t)=limΔt→0vср.
Итак, v=limΔt→0ΔsΔt
Задача 2 (о касательной к графику функции). Дан график функции y=f(x). На нем выбрана точка M(a;f(a)), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
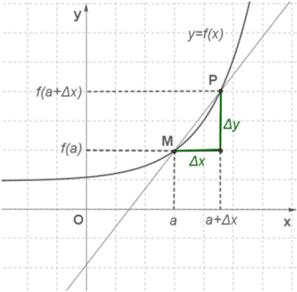
Решение . Дадим аргументу приращение Δx и рассмотрим на графике точку P с абсциссой a+Δx. Ордината точки P равна f(a+Δx). Угловой коэффициент секущей MP, т. е. тангенс угла между секущей и осью x, вычисляется по формуле kсек=ΔyΔx.
Если мы теперь устремим Δx к нулю, то точка P начнет приближаться по кривой к точке M. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной kкас=limΔx→0kсек будет вычисляться по формуле kкас=limΔx→0kсек. Используя приведенную выше формулу для kсек, получаем: kкас=limΔx→0ΔyΔx
|
|
|
2. Определение производной, ее геометрический, механический и экономический смысл. Связь между непрерывностью и дифференцируемостью функции.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
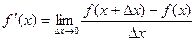
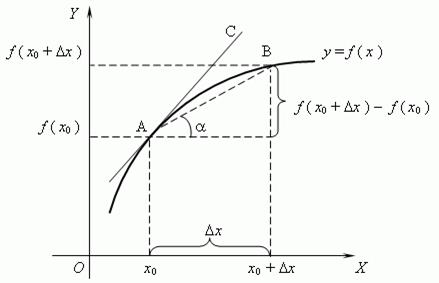
Пусть f(x) определена на некотором промежутке (a, b). Тогда 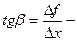 тангенс угла наклона секущей АВ к графику функции.
тангенс угла наклона секущей АВ к графику функции.
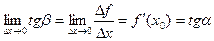 , где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
, где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: 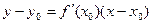
Уравнение нормали к кривой: 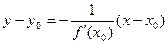 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
Экономический смысл производной: Пусть y=u(t) выражает объем произведенной продукции y за время t . Тогда ее производная  по смыслу есть скорость изменения объема продукции в данный момент времени, т.е. то, что называется производительностью труда в момент времени t0.
по смыслу есть скорость изменения объема продукции в данный момент времени, т.е. то, что называется производительностью труда в момент времени t0.
|
|
|
Связь между дифференцируемостью и непрерывностью функции
Теорема. Если функция y=f(x) дифференцируема в точке x, то она и непрерывна в этой точке. Обратное не гарантировано.
3. Правила и формулы дифференцирования.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3) 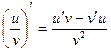 , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9) 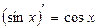
2)(xm)¢ = mxm-1; 10) 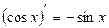
3) 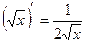 11)
11) 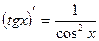
4) 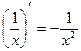 12)
12) 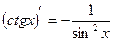
5) 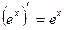 13)
13) 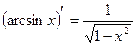
6) 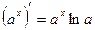 14)
14) 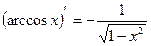
7) 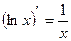 15)
15) 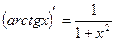
8) 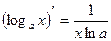 16)
16) 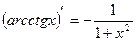
Контрольные вопросы:
- Сформулируйте определение производной функции. Что такое дифференцирование функции?
- Какая функция называется дифференцируемой?
- Сформулируйте общее правило нахождения производной функции.
- В чем заключается геометрический смысл производной?
- В чем заключается физический смысл производной?
- В чем заключается экономический смысл производной?
- Перечислите правила нахождения производной функции.
|
|
|
Дата добавления: 2019-07-15; просмотров: 169; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
