Тема 2. Функция. Предел функции
Лекция5. Функция.
Основные вопросы:
1. Понятие функции.
2. Основные свойства функций.
3. Классификация функций.
Обзор лекции:
В данной лекции рассматриваются понятие функции, способы задания функции, основные свойства функции: монотонность, четность, ограниченность, периодичность; классификация функций.
1. Понятие функции.
При изучении определённых процессов реального мира мы встречаемся с характеризующими их величинами, которые меняются во время изучения этих процессов. При этом изменение одной величины сопутствует изменению другой.
Определение. Если каждому элементу х множества Х (называемого областью определения функции) по определенному закону ставится в соответствие единственный элемент у множества Y, то подобное отображение называется функцией, определенной на множестве Х со значениями в множестве Y. При этом х называется независимой переменной, или аргументом, а у = f(x) – зависимой переменной, или функцией.
Множество Х называется областью определения функции f и обозначается D(f). Множество всех уÎY называется множеством значений функции f и обозначается E(f).
Если элементами множеств Х и Y являются действительные числа, то функцию f называют числовой функцией.
Способы задания функции:
1) Аналитический. Аналитический способ появился с введением систем координат и принятием символической записи различных законов в виде одной формулы у = f(x) или их совокупности.
|
|
|
2) графический. Говорят, что функция задана графически, если начерчен ее график. Совокупность точек, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции у, называется графиком данной функции
3) табличный. Для некоторых значений переменной x указываются соответствующие значения переменной y. Примерами такого способа заданий являются таблицы значений тригонометрических функ-ций, таблицы, представляющие собой зависимость между измеряемыми величинами и др.
2. Основные свойства функции.
Рассмотрим основные свойства функций.
Четность и нечетность. Пусть область определения функции симметрична относительно нулевой точки, кроме, может быть, самой точки 0.
Функция 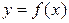 называется четной, если
называется четной, если 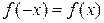 , для любого х из области определения.
, для любого х из области определения.
Например, функции 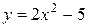 ,
, 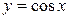 , определенные на всей числовой прямой, и функция
, определенные на всей числовой прямой, и функция 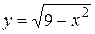 , определенная на отрезке
, определенная на отрезке 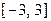 , являются четными, поскольку для них выполняется условие
, являются четными, поскольку для них выполняется условие 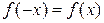 :
: 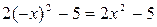 ;
; 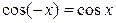 ;
; 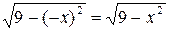 .
.
График четной функции симметричен относительно оси 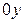 (например, график функции
(например, график функции 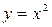 ).
).
Функция 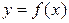 называется нечетной, если
называется нечетной, если  , для любого х из области определения.
, для любого х из области определения.
|
|
|
Функции, для которых не выполняются условия 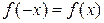 и
и  , называются функциями общего вида.
, называются функциями общего вида.
Монотонность. Функция 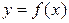 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке 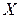 , если для любых двух точек
, если для любых двух точек 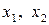 этого промежутка таких, что
этого промежутка таких, что 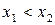 , выполняется неравенство
, выполняется неравенство 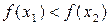 (
( 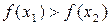 ) (иными словами, если большему значению аргумента соответствует большее (меньшее) значение функции). Если в приведенном выше определении выполняется неравенство
) (иными словами, если большему значению аргумента соответствует большее (меньшее) значение функции). Если в приведенном выше определении выполняется неравенство 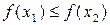 (
( 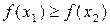 ), то функция называется неубывающей (невозрастающей).
), то функция называется неубывающей (невозрастающей).
Возрастающие, неубывающие, убывающие и невозрастающие функции называются монотонными. Возрастающие и убывающие функции еще называются строго монотонными.
Например, функция 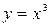 монотонно возрастает на всей числовой прямой; функция
монотонно возрастает на всей числовой прямой; функция 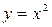 – кусочно монотонная: на
– кусочно монотонная: на 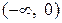 она убывает, а на
она убывает, а на 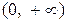 – возрастает.
– возрастает.
Ограниченность. Функция 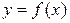 , определенная на множестве
, определенная на множестве 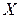 , называется ограниченной сверху (снизу), если существует такое число
, называется ограниченной сверху (снизу), если существует такое число 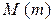 , что при всех значениях аргумента
, что при всех значениях аргумента 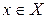 выполняется неравенство
выполняется неравенство 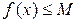 (
( 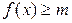 ).
).
Если функция ограничена сверху или снизу, то говорят, что функция ограничена, т.е. 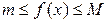 .
.
Выберем из чисел 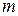 и
и 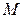 то, модуль которого больше. Пусть это будет
то, модуль которого больше. Пусть это будет 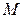 . Тогда
. Тогда 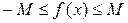 , или
, или 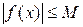 .
.
График ограниченной сверху (снизу) функции лежит ниже (выше) прямой 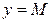 (
( 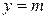 ), а график ограниченной функции размещается в полосе между прямыми
), а график ограниченной функции размещается в полосе между прямыми 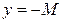 и
и 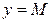 .
.
|
|
|
Например, функция 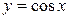 ограничена на всей числовой оси, ибо
ограничена на всей числовой оси, ибо 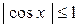 , для любого
, для любого 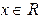 .
.
Периодичность. Функция 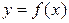 называется периодической, если существует такое действительное число
называется периодической, если существует такое действительное число 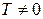 , что для любых
, что для любых 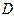 из области определения функции
из области определения функции
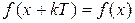 ,
,
где 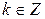 . Число
. Число 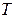 называется периодом. Наименьший из положительных периодов функции называется основным периодом функции.
называется периодом. Наименьший из положительных периодов функции называется основным периодом функции.
Например, для функций 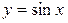 и
и 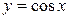 число
число 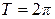 является основным периодом. Для функций
является основным периодом. Для функций 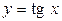 ,
, 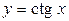 основным периодом является число
основным периодом является число 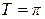 .
.
Нули функции. Нулем функции называется такое действительное значение 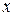 , при котором значение функции равно нулю.
, при котором значение функции равно нулю.
Для того, чтобы найти нули функции, следует решить уравнение 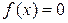 . Действительные корни этого уравнения являются нулями функции
. Действительные корни этого уравнения являются нулями функции 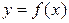 , и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пересекает ось абсцисс, либо касается ее, либо имеет общую точку с этой осью. Функция может и не иметь нулей. Такова, например, функция
, и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пересекает ось абсцисс, либо касается ее, либо имеет общую точку с этой осью. Функция может и не иметь нулей. Такова, например, функция 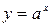 .
.
3. Классификация функций.
Основные элементарные функции.
1) Степенная функция у = хα, 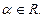
2) Показательная функция у = ах, a > 0, a 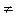 1.
1.
|
|
|
3) Логарифмическая функция y=logax, a > 0, a 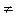 1.
1.
4) Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x.
5) Обратные тригонометрические функции: y = arcsin x, y = arсcos x, y = arctg x, y = arcctg x, y = arcsec x, y = arccosec x.
Определение. Элементарной функцией y = f(x) называется функция, заданная с помощью основных элементарных функций и постоянных с помощью конечного числа арифметических операций и взятия функции от функции.
Определение. Если у=F(u) является функцией от u, a u=φ(x) – функцией от х, то у = F[φ(x)] называется сложной функцией или функцией от функции.
Определение. Если для функции у = f(х) можно определить функцию х = g(у), ставящую в соответствие каждому значению функции у = f(x) значение ее аргумента х, то функция у = g(x) называется обратной функцией к у = f(x) и обозначается y = f–1(x).
Контрольные вопросы:
1. Что называется функцией?
2. Что называется областью определения и областью значений функции?
3. Перечислите способы задания функции.
4. Перечислите основные свойства функции
5. Перечислите основные элементарные функциии.
6. Какая функция называется неявной?
7. Какая функция называется сложной?
Лекция 6. Пределы функций.
Основные вопросы:
1. Предел функции в бесконечности и точке.
2. Основные теоремы о пределах.
- Бесконечно малые величины и бесконечно большие величины, их свойства.
Обзор лекции:
В данной лекции рассматриваются понятия предела функции в точке и бесконечности, основные теоремы о пределах, бесконечно малые величины и бесконечно большие величины, их свойства.
1. Предел функции в бесконечности и точке.
Определим понятие окрестности точки х0 как множество значений х, являющихся решениями неравенства 0<|x - x0| < δ, где δ > 0 – некоторое число. Само значение х0 может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой).
Пусть функция у = f(x) определена в некоторой окрестности точки х0.
Определение. Число А называется пределом функции у = f(x) при х, стремящемся к х0, если 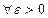
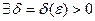 такое, что |f(x) - A| < ε при |x - x0| < δ. Обозначение:
такое, что |f(x) - A| < ε при |x - x0| < δ. Обозначение: 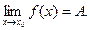 .
.
Замечание. Для существования предела функции в точке х0 не требуется, чтобы функция была определена в самой этой точке.
Определение. Функция у = f(x) имеет бесконечный предел при х, стремящемуся к х0 (стремится к бесконечности, является бесконечно большой), если 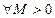
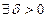 такое, что |f(x)| > M при |x - x0| < δ.
такое, что |f(x)| > M при |x - x0| < δ.
Обозначение: 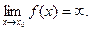
Определение. Число А называется пределом функции y = f(x) на бесконечности, если 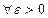
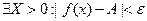 при x > X (
при x > X ( 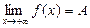 ), при x < -X (
), при x < -X ( 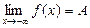 ), при |x| > X (
), при |x| > X ( 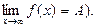
Свойства пределов.
1. Если существует 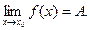 (А – конечное число), то функция у = f(x) является ограниченной в некоторой окрестности (возможно, проколотой) точки х0.
(А – конечное число), то функция у = f(x) является ограниченной в некоторой окрестности (возможно, проколотой) точки х0.
2. Функция не может иметь двух различных пределов при х, стремящемуся к одному и тому же значению.
- Если
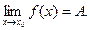 и А
и А 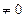 , то существует окрестность точки х0, в которой функция f(x) сохраняет постоянный знак ( f(x)>0, если A > 0, и f(x)<0, если A < 0).
, то существует окрестность точки х0, в которой функция f(x) сохраняет постоянный знак ( f(x)>0, если A > 0, и f(x)<0, если A < 0).
2. Основные теоремы о пределах.
Теорема. Если существуют 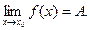 и
и 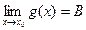 , то существует и
, то существует и 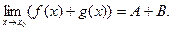
Теорема. Если существуют 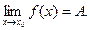 и
и 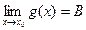 , то существует и
, то существует и 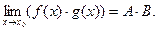
Теорема. Если существуют 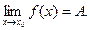 и
и 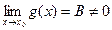 , то существует и
, то существует и
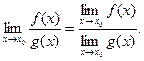
Теорема Если f(x) ≤ φ(x) ≤ g(x) в некоторой окрестности х0 и 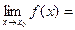
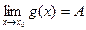 , то существует и
, то существует и 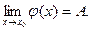 .
.
Теорема. Если при х→х0 f(x)≥0 и 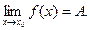 , то А≥0.
, то А≥0.
Следствие 1. Аналогично доказывается, что если f(x)≤0, то А≤0.
Следствие 2. Если f(x)≥g(x) и обе функции имеют пределы в точке х0, то 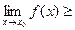
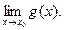
Замечание. Все перечисленные утверждения можно доказать для 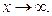
Теорема (без доказательства). Ограниченная и возрастающая при a<x<b (a<x< 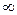 ) функция имеет предел при х
) функция имеет предел при х 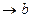 (х
(х 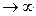 ).
).
- Бесконечно малые величины и бесконечно большие величины, их свойства.
Определение. Функция у=α(х) называется бесконечно малой при х→х0, если 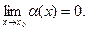
Свойства бесконечно малых.
1. Сумма двух бесконечно малых есть бесконечно малая.
Замечание. Отсюда следует, что сумма любого конечного числа бесконечно малых есть бесконечно малая.
2. Если α(х) – бесконечно малая при х→х0, а f(x) – функция, ограниченная в некоторой окрестности х0, то α(х)f(x) – бесконечно малая при х→х0.
Следствие 1. Произведение бесконечно малой на конечное число есть бесконечно малая.
Следствие 2. Произведение двух или нескольких бесконечно малых есть бесконечно малая.
Следствие 3. Линейная комбинация бесконечно малых есть бесконечно малая.
3. Если 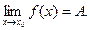 , то необходимым и достаточным условием этого является то, что функцию f(x) можно представить в виде f(x)=A+α(x), где α(х) – бесконечно малая при х→х0.
, то необходимым и достаточным условием этого является то, что функцию f(x) можно представить в виде f(x)=A+α(x), где α(х) – бесконечно малая при х→х0.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Определение. Если 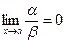 , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если 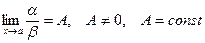 , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 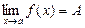 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то
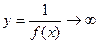
Контрольные вопросы:
- Дайте определение предела функции в точке.
- Доказать, что функция f(x)=3x-1 при х→1 имеет предел, равный 2.
- Сформулируйте основные теоремы о пределах.
- Какие величины называются бесконечно большими, бесконечно малыми?
- Сформулируйте свойства бесконечно больших, бесконечно малых.
Дата добавления: 2019-07-15; просмотров: 186; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
