Лекция 7. Раскрытие неопределенностей
Основные вопросы:
1. Раскрытие неопределенностей различных типов.
2. Замечательные пределы.
3. Эквивалентные бесконечно малые и их применение для вычисления пределов.
Обзор лекции:
В данной лекции рассматриваются основные виды неопределенностей, способы раскрытия различных типов неопределенностей, применение замечательных пределов и эквивалентных бесконечно малых величин при нахождении пределов функции.
1. Раскрытие неопределенностей различных типов.
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю.
Условные выражения 
характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.
Рассмотрим некоторые приемы раскрытия неопределенностей.
| Вид неопределенности | Вид выражения, расположенного под знаком предела | Способ раскрытия неопределенности |
I. 
| · Если в числителе и знаменателе многочлены (степенные функции) · Если в числителе и знаменателе иррациональные функции · Если в числителе и знаменателе показательные функции | Числитель и знаменатель дроби почленно делят на  в старшей степени
числитель и знаменатель почленно делят на в старшей степени с учетом степеней корней
|
| II. | · Если в числителе и знаменателе многочлены | Числитель и знаменатель дроби раскладывают на множители (с целью сократить дробь) |
· Если числитель (или знаменатель) дроби содержат иррациональность (  )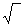
| Числитель и знаменатель дроби умножают на выражение, сопряженное тому, что содержит иррациональность | |
| · Если числитель (или знаменатель) дроби содержат тригонометрические или обратные тригонометрические функции | Для раскрытия неопределенности используют первый замечательный предел | |
III.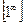 
| Для раскрытия неопределенности используют второй замечательный предел |
2. Замечательные пределы.
Теорема (первый замечательный предел). 
.
Cледствия из первого замечательного предела.
1. 
2. 
3. 
5. 
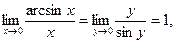где y = arcsinx.
6. 
где y = arctgx.
Теорема (второй замечательный предел). 
.
3. Эквивалентные бесконечно малые и их применение для вычисления пределов.
Определение. Если 
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Найти предел 
Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
Теорема. Предел отношения двух б.м. функций равен пределу отношения эквивалентных им б.м. функций, то есть верны предельные равенства:
Контрольные вопросы:
- Какие виды неопределённостей вам известны?
- Что значит раскрыть неопределённость?
- Как раскрыть неопределённость , когда в числители и знаменатели стоят целые рациональные выражения?
- Как раскрыть неопределённость
, когда в числители и знаменатели стоят целые рациональные выражения? - Как раскрыть неопределённость , когда в числители и знаменатели стоят иррациональные выражения?
- Запишите Ι и ΙΙ замечательные пределы.
- Каким образом можно применять эквивалентные б.м. функции при вычислении пределов?
Дата добавления: 2019-07-15; просмотров: 510; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!