Лекция 15-16. Приложение производной

Основные вопросы:

1. Признаки возрастания и убывания функций.

2. Экстремумы функций. Схема нахождения интервалов монотонности и экстремумов функции.

3. Наибольшее и наименьшее значение функции на отрезке.

4. Выпуклость графика функции. Точки перегиба.

5. Асимптоты графика функции.

6. Полное исследование функции и построение графика

 

Обзор лекции:

В данной лекции рассматриваются условия монотонности функции; существования экстремума; наибольшее и наименьшее значение функции на отрезке, выпуклость и вогнутость функции; точки перегиба, асимптоты функции; общая схема исследования функции.

 

1. Признаки возрастания и убывания функций.

Определение. Функция y = f(x) называется возрастающей (убывающей) на [ab], если  таких, что x₁ < x₂, f(x₁) < f(x₂) ( f(x₁) > f(x₂) ).

Теорема. Если функция f(x), дифференцируемая на [ab], возрастает на этом отрезке, то 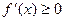 на [ab].

Если f(x) непрерывна на [ab] и дифференцируема на (ab), причем  для a < x < b, то эта функция возрастает на отрезке [ab].

 

2. Экстремумы функций. Схема нахождения интервалов монотонности и экстремумов функции.

 

Теорема (необходимое условие экстремума). Пусть функция f(x) задана в некоторой окрестности точки х₀. Если х₀ является точкой экстремума функции, то 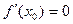 или не существует.

Примеры.

1. Функция y = x² имеет минимум при х = 0, причем (х²)′ = 2x = 0 при х = 0.

2. Минимум функции y = |x| достигается при х = 0, причем производная в этой точке не существует.

Замечание. Отметим еще раз, что теорема дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′(x) = 0, функция достигает экстремума.

Пример. У функции  y = x³ y ′ = 3x² = 0 при х = 0, однако функция монотонно возрастает во всей области определения.

Определение. Если функция определена в некоторой окрестности точки х₀  и ее производная в этой точке равна нулю или не существует, точка х₀ называется критической точкой функции. Теорема означает, что все точки экстремума находятся в множестве критических точек функции.

Теорема (Достаточные условия экстремума). Пусть функция f(x)  непрерывна в некоторой окрестности точки х₀, дифференцируема в проколотой окрестности этой точки и с каждой стороны от данной точки  f ′(x) сохраняет постоянный знак. Тогда:

1) если  f ′(x) > 0 при x < x₀ и f ′(x) < 0 при x > x₀ , точка х₀  является точкой максимума;

2) если  f ′(x) < 0 при x < x₀ и f ′(x) > 0 при x > x₀ , точка х₀  является точкой минимума;

3) если f ′(x) не меняет знак в точке х₀ , эта точка не является точкой экстремума.

Теорема. Пусть f ′(x₀) = 0 и у рассматриваемой функции существует непрерывная вторая производная в некоторой окрестности точки х₀. Тогда х₀  является точкой максимума, если f ′′(x₀) < 0, или точкой минимума, если f ′′(x₀) > 0.

Схема исследования функции f(х) на экстремум и монотонность:

1. Найти производную у′(х).

2. Найти стационарные и критические точки функции.

З. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремума функции.

4. Найти экстремумы (экстремальные значения) функции.

 

3. Наибольшее и наименьшее значение функции на отрезке.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке :

1. найти ;
2. найти точки, в которых или не существует, и отобрать из них те, что лежат внутри отрезка ;
3. вычислить значения функции в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции на отрезке , которые можно обозначить так: .

 

4. Выпуклость графика функции. Точки перегиба.

 

Определение. Кривая называется выпуклой (обращенной выпуклостью вверх) на интервале (ab), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Определение. . Кривая называется вогнутой (обращенной выпуклостью вниз) на интервале (ab), если все точки кривой лежат выше любой ее касательной на этом интервале.

Теорема.  Если f ′′(x) < 0 во всех точках интервала (ab), то кривая y = f(x) выпукла на этом интервале. Если f ′′(x) > 0 во всех точках интервала (ab), то кривая y = f(x) вогнутаа на этом интервале.

Определение.  Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба.

Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую – ниже.

Теорема (необходимое условие точки перегиба). Если в точке x₀ перегиба кривой, являющейся графиком функции  y = f(x), существует вторая производная  f ′′(x), то         f ′′(x₀) = 0.

Теорема (достаточное условие точек перегиба). Если функция y = f(x) дифференцируема в точке х₀ , дважды дифференцируема в проколотой окрестности этой точки и f ′′(x)  меняет знак при х = х₀ , то х₀ – точка перегиба.

Пример. Найдем интервалы выпуклости и вогнутости и точки перегиба функции           y = x³ -6x² + x – 12. y′ = 3x² - 12x + 1, y′′ = 6x – 12. y′′ = 0 при х = 2, y′′ < 0 при х < 2, y′′ > 0 при х > 2. Таким образом, график функции является выпуклым при  х < 2, вогнутым при х > 2, а х = 2 – точка его перегиба.

 

5. Асимптоты функции.

 

Определение. Прямая называется асимптотой графика функции y = f(x) , если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность.

Рассмотрим три вида асимптот и определим способы их нахождения.

1. Вертикальные асимптоты – прямые, задаваемые уравнениями вида  х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен.                                   Пример. Вертикальной асимптотой графика функции y = 1/x является прямая    х = 0, то есть ось ординат.

2.  Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при  или при  конечен, т.е. .

3. Наклонные асимптоты – прямые вида  y = kx + b. Найдем k и b. Поскольку при , , если этот предел существует, конечен и не равен нулю. Однако даже при выполнении этих условий наклонная асимптота может не существовать. Для ее существования требуется, чтобы имелся конечный предел при  разности  f(x) – kx. Этот предел будет равен b , так как при .

Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при  и при ).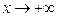

 

6. Общая схема исследования функции.

Результаты, полученные при изучении различных аспектов поведения функции, позволяют сформулировать общую схему ее исследования с целью построения качественного графика, отражающего характерные особенности поведения данной функции. Для этого требуется определить:

1) область определения функции и ее поведение на границах области определения (найти соответствующие односторонние пределы или пределы на бесконечности);

2) четность и периодичность функции;

3) интервалы непрерывности и точки разрыва (указав при этом тип разрыва);

4) нули функции (т.е. значения х , при которых f(x) = 0) и области постоянства знака;

5) интервалы монотонности и экстремумы;

6) интервалы выпуклости и вогнутости и точки перегиба;

7) асимптоты графика функции.

 

Контрольные вопросы:

1. Сформулируйте достаточное условие возрастания и убывания функции.

2. Сформулируйте определение экстремумов функции.

3. Сформулируйте необходимое и достаточное условия существования экстремума.

4. Сформулируйте определение выпуклости и вогнутости функции.

5. Сформулируйте необходимое и достаточное условия точек перегиба.

6. Что такое асимптота функции? Какие асимптоты бывают?

7. Сформулируйте определения вертикальной, горизонтальной, наклонной асимптот.

8. Общая схема исследования функций

---

Дата добавления: 2019-07-15; просмотров: 141; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!