Устойчивость по Вышнеградскому

Вышнеградский И.А. предложил изображать границу устойчивости на так называемой плоскости параметров Вышнеградского.

Пусть имеем характеристическое уравнение третьей степени.

Преобразуем его с помощью подстановки:

Тогда оно примет вид:

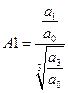
A₁ и A₂ называются параметрами Вышнеградского (безразмерные величины), в плоскости которых строится граница устойчивости.

Применим к преобразованному уравнению критерий устойчивости Гурвица

 

 

или A₁ A₂ > 1

На границе устойчивости .

Отсюда - уравнение на границе устойчивости

По коэффициентам характеристического уравнения определяются А₁ и А₂ . Если точка оказалась ниже гиперболы – САУ устойчива, выше - неустойчива.

 

Устойчивость по Гурвицу

В 1895 г. швейцарским ученым А. Гурвицем был предложен критерий, определяющий условия, которым должны удовлетворять коэффициенты характеристического уравнения системы для обеспечения отрицательности вещественных частей корней ее характеристического уравнения.

На основании характеристического уравнения системы

.

строится определитель Гурвица (при ).

Свободные места заполняются нулями.

Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительны.

Диагональные миноры:

;     ;      ; . . .

 

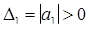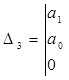
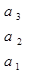
Для устойчивости системы третьего порядка необходимо и достаточно кроме положительности всех коэффициентов характеристического уравнения выполнение неравенства: .

1) если определители матрицы и всех диагональных миноров положительны, то система устойчива;

2) если определитель или хотя бы один минор равен нулю, то система находится на границе устойчивости;

3) если определитель или хотя бы один минор отрицательны, то система неустойчива.

Устойчивость по Михайлову

Критерий устойчивости Михайлова относится к частотным критериям и используется для исследования устойчивости замкнутых систем

Формулировка критерия Михайлова.

Для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно чтобы годограф Михайлова при изменении частоты от 0 до , начинался при на вещественной положительной полуоси, обходил последовательно квадрантов координатной плоскости против часовой стрелки, где - порядок характеристического полинома. вании принципа аргумента формулируется критерий Михайлова:

 Для устойчивости системы необходимо и достаточно, чтобы корни мни-мой и вещественной частей годографа Михайлова перемежались.

Если корни не перемежаются, то система неустойчива.

Если характеристическое уравнение не имеет какого либо члена, то система также неустойчива.

 

Устойчивость по Найквисту

Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ) разомкнутой системы

Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой (а. ф. х.) или логарифмических частотных характеристик (л. ч. х.) разомкнутой системы.

Для того, чтобы замкнутая система автоматического регулирования была устойчива необходимо и достаточно, чтобы приращение фазы F(jw) при изменении от 0 до  равнялась М( ).М- число корней харак-го уравнения замкнутой системы, а также годограф охватывал точку ( )

 

 

Форсирующее звено

Данное звено используется в системах автоматического управления для целей коррекции. Его передаточная функция имеет вид:

;

Частотные характеристики:

АФЧХ: ; ВЧХ: ;

МЧХ: ; ФЧХ: ; ; при .

АЧХ: .

ЛАХ: ;

Для построения ЛАХ форсирующего звена рассматриваются области низких частот НЧ и высоких частот ВЧ:

НЧ: ; ;

ВЧ: ; .

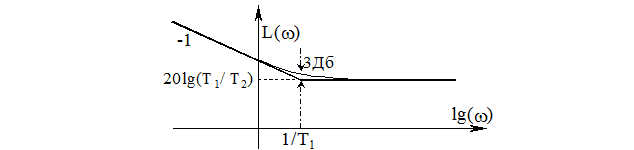
Точка пересечения ЛАХ оси ординат определяется как:

.

 

 

Частотные характеристики

Важными динамическими характеристиками объекта являются его частотные характеристики, которые определяют взаимо­связь между параметрами периодических сигналов на входе и вы­ходе. Чаще всего их используют для описания одноканальных объ­ектов:

Если на его вход подавать гармонический сигнал заданной ам­плитуды А₁ и частоты ω,

и = A₁cos ωt,

то на выходе в установившемся режиме у устойчивого объекта будет также гармонический сигнал той же частоты, но в об­щем случае другой амплитуды со сдвигом по фазе

у = А₂cos(ωt + φ).

Для нахождения соотношения между входным и выходным гар­моническими сигналами можно воспользоваться передаточной функцией (2.38), из которой формальной заменой р на jω получим обобщенную частотную характеристику

Составляющие обобщенной частотной характеристики W(jω) имеют самостоятельное значение и следующие названия:

R(ω) - вещественная частотная характеристика (ВЧХ),

I(ω) - мнимая частотная характеристика (МЧХ),

A (ω) - амплитудная частотная характе­ристика (АЧХ),

φ(ω)- фазовая частотная характеристика (ФЧХ).

Для исследования частотных свойств объекта или системы удобно использовать графическое представление частотных харак­теристик. В этом случае обобщенная частотная характеристика W(jω) может быть построена на комплексной плоскости в соот­ветствии с выражением (2.40), когда каждому значению частоты ω₁, соответствует вектор W(jω_i).

При изменении ω от 0 до ∞ ко­нец этого вектора «прочерчи­вает» на комплексной плоско­сти кривую, которая называет­ся амплитудно-фазовой ха­рактеристикой (АФХ).

Наряду с амплитудно-фазо­вой характеристикой (рис. 2.8) также строится все остальные частотные характе­ристики. Так, амплитудная частотная характеристика по­казывает, как звено пропускает

Сигналы различной частоты; причем оценкой пропускания является отношение амплитуд выходного (А₂) и входного сигналов (А₁). Фазовая частотная характеристика отражает фазовые сдвиги, вносимые системой на различных частотах.

 

---

Дата добавления: 2019-02-22; просмотров: 1612; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!