Типовое пропорциональное звено
Пропорциональными(Усилительным, безинерционным) называют такие звенья, у которых уравнения динамики не отличается от уравнений статики. В этих звеньях приращение выходной величины прямо пропорционально приращению входной: Хвых=К*Хвх.
W(jw)=K;
P(w)=K; Q(w)=0;
A(w)=K;
j(w)=0;
L(w)=20lgK;
h(t)=K1(t); g(t)=Ld(t)
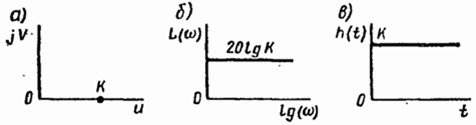
Типовое реальное дифференцирующее звено
Дифференцирующим называется звено, в котором выходная величина пропорциональна скорости изменения выходной величины, т.е пропорциональна ее производной. Дифференцирующее звено иногда называют изодромным.
Различают идеальное и реальное дифференцирующие звенья.
Дифференциальное уравнение и передаточная функция такого звена имеют вид: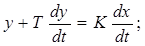 
.
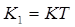Амплитудно-фазовая частотная характеристика реального дифференцирующего звена: 
;
АЧХ: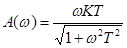 
; ЛАХ: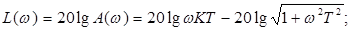 
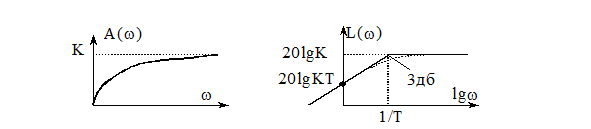
ФЧХ: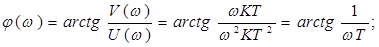 
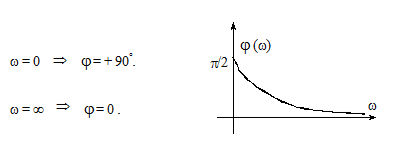
Переходная характеристика:
ℒ 
;
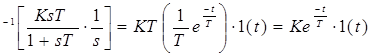Весовая функция: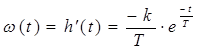 
.
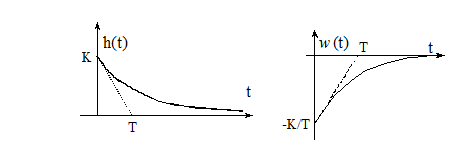
Типовое реальное интегрирующее звено
Интегрирующем называется звено, в котором скорость изменения выходной величины пропорциональна входной величине или, иначе, выходная величина пропорциональна интегралу по времени от входной величины. Интегрирующее звено так же называется астатическим.
Различают идеальное и реальное интегрирующее звенья.
Динамика процесса в таком звене описывается следующим уравнением:
,
где k – коэффициент усиления.
1. Переходная характеристика:
|
|
|
2. Импульсная переходная характеристика:
3. Передаточная функция реального интегрирующего звена:
Реальное интегрирующее звено представляет собой последовательное соединение идеального интегрирующего звена и апериодического.
4. АФХ:
5. АЧХ:
6. ФЧХ:
7. ЛАЧХ:
Типовое усилительное звено
Усилительное звено-выходная величина воспроизводит без запаздывания входную величину
У этого звена выходная величина y(t) пропорциональна входной. Поэтому усилительное звено называют еще пропорциональным. Математическая модель
y(t) = k x(t) ,
где константа k - коэффициент усиления звена.
Операторное уравнение
Y(p) = k X(p) .
Передаточная функция представляет собой коэффициент усиления:
W(p) =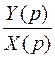 
= k .
Комплексная частотная характеристика имеет только действительную часть:
W(jw) = k .
W(jw) = P(w) + j Q(w). Действительная частотная характеристика P(w) = k, мнимая частотная характеристика Q(w) = 0.
Амплитудная частотная характеристика:
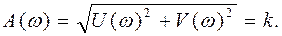
Фазовая частотная характеристика:
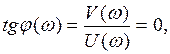
φ (ω) = arctg 0 = 0.
Фазовый сдвиг отсутствует.
Логарифмическая амплитудная частотная характеристика имеет вид:
L (ω) = 20lg A (ω) = 20lg k .
От ω, следовательно и от lgω, не зависит.
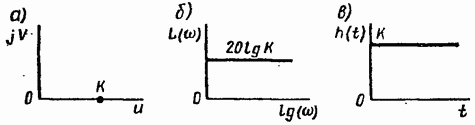
Типовые воздействия
|
|
|
Воздействием называется какой-либо фактор, влияющий на работу системы автоматического управления.
Виды воздействия: задающее, управляющее, возмущающее.
Задающем называется вводимое в систему воздействие, определяющее необходимый закон изменения управляемой величины.
Управляющим называется воздействие, которое обеспечивает изменение управляемой величины по заданному закону. Управляющее воздействие формируется в системе с помощью задающего воздействия.
Возмущающим называется воздействие, которое нарушает заданный закон изменения управляемой величины. К возмущающим воздействиям относятся нагрузка объекта управления, изменения внешних условий, изменения во времени свойств отдельных элементов системы.
Сигналы на входе звена – произвольная временные функции. Чтобы иметь возможность изучать поведение звеньев при прочих равных условиях вводится 3 вида регулярных сигналов:
1. Единичное ступенчатое воздействие
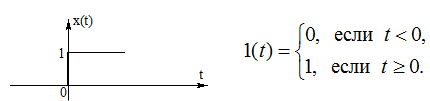
2. Импульсный сигнал
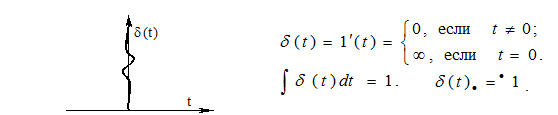
Реально 
- импульс достаточно короткий с крутыми фронтами.
3. Гармоничный сигнал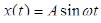 
.
Типовые звенья
Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.
|
|
|
Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.
Звенья, описываемые алгебраическими уравнениями:
- усилительное (пропорциональное),
- запаздывающее.
Звенья, описываемые дифференциальным уравнением первого порядка:
- интегрирующее,
- дифференцирующее.
Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательным или апериодическим.
Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.
Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.
|
|
|
Уравнения динамики и статики
Поведение системы в установившемся состоянии определяется уравнениями статики, или статическими характеристиками. Под статической характеристикой понимают зависимость между входной хвх и выходной хвых величинами системы в равновесном состоянии
хвых =f(хвх)
Обычно уравнения статики являются алгебраическими.
Поведение системы в неравновесном состоянии или в переходном процессе описывается уравнениями динамики. В общем виде уравнение динамики или динамическая характеристика системы с входной хвх и выходной хвых величинами представляет собой зависимость типа
хвых = f (хвх, t )
которая, как правило, представляет собой дифференциальное: уравнение. Прохождение сигнала по каналам системы характеризуется своими уравнениями статики и динамики.
Дата добавления: 2019-02-22; просмотров: 375; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!