Типовое идеальное интегральное звено

 Динамика интегрирующего звена описывается дифференциальным уравнением

.

1. Переходная характеристика:

2. Импульсная переходная характеристика (или функция веса) имеет вид:

3. Передаточная функция идеального интегрирующего звена:

4. АФХ звена:

на комплексной плоскости изображается в виде прямой, совпадающей с мнимой осью.

5. АЧХ:

представляет собой гиперболу, которая при стремится к бесконечности. При увеличении частоты значения А(w) стремятся к нулю. Это свойство сближает интегрирующие звенья с инерционными.

6. ФЧХ идеального интегрирующего звена:

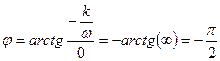
показывает, что сдвиг фаз, создаваемый звеном, на всех частотах одинаков и равен

-90⁰.

7. ЛАЧХ:

представляет собой прямую с наклоном –20дБ/декаду, проходящую через точку с координатами w=1, L(w)=20lgk.

 

 

Типовое идеальное интегрирующее звено

Интегрирующем называется звено, в котором скорость изменения выходной величины пропорциональна входной величине или, иначе, выходная величина пропорциональна интегралу по времени от входной величины. Интегрирующее звено так же называется астатическим.

Различают идеальное и реальное интегрирующее звенья.

Динамика интегрирующего звена описывается дифференциальным уравнением

.

1. Переходная характеристика:

2. Импульсная переходная характеристика (или функция веса) имеет вид:

3. Передаточная функция идеального интегрирующего звена:

4. АФХ звена:

на комплексной плоскости изображается в виде прямой, совпадающей с мнимой осью.

5. АЧХ:

представляет собой гиперболу, которая при стремится к бесконечности. При увеличении частоты значения А(w) стремятся к нулю. Это свойство сближает интегрирующие звенья с инерционными.

6. ФЧХ идеального интегрирующего звена:

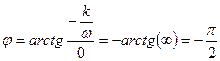
показывает, что сдвиг фаз, создаваемый звеном, на всех частотах одинаков и равен

-90⁰.

7. ЛАЧХ:

представляет собой прямую с наклоном –20дБ/декаду, проходящую через точку с координатами w=1, L(w)=20lgk.

 

Типовое интегрирующее звено

Интегрирующем называется звено, в котором скорость изменения выходной величины пропорциональна входной величине или, иначе, выходная величина пропорциональна интегралу по времени от входной величины. Интегрирующее звено так же называется астатическим.

Различают идеальное и реальное интегрирующее звенья.

Динамика интегрирующего звена описывается дифференциальным уравнением

.

1. Переходная характеристика:

2. Импульсная переходная характеристика (или функция веса) имеет вид:

3. Передаточная функция идеального интегрирующего звена:

4. АФХ звена:

на комплексной плоскости изображается в виде прямой, совпадающей с мнимой осью.

5. АЧХ:

представляет собой гиперболу, которая при стремится к бесконечности. При увеличении частоты значения А(w) стремятся к нулю. Это свойство сближает интегрирующие звенья с инерционными.

6. ФЧХ идеального интегрирующего звена:

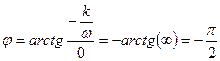
показывает, что сдвиг фаз, создаваемый звеном, на всех частотах одинаков и равен

-90⁰.

7. ЛАЧХ:

представляет собой прямую с наклоном –20дБ/декаду, проходящую через точку с координатами w=1, L(w)=20lgk.

 

Реальное интегрирующее звено

Динамика процесса в таком звене описывается следующим уравнением:

,

где k – коэффициент усиления.

1. Переходная характеристика:

2. Импульсная переходная характеристика:

3. Передаточная функция реального интегрирующего звена:

Реальное интегрирующее звено представляет собой последовательное соединение идеального интегрирующего звена и апериодического.

4. АФХ:

5. АЧХ:

6. ФЧХ:

7. ЛАЧХ:

 

Типовое колебательное звено

Колебательным называется звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величина стремится к новому установившемуся значению, совершая затухающие колебания.

Переходный процесс такого звена описывается дифференциальным уравнением второго порядка.

или

где T₁ и T₂ – постоянные времени колебательного звена, имеющие размерность времени;

коэффициент усиления (передачи) звена;

T – эквивалентная постоянная времени звена

;

– постоянная безразмерная величина, называемая относительным коэффициентом затухания колебательного звена .

Операторные уравнения колебательного звена:

Переходные функции колебательного звена:

Характеристические уравнения колебательного звена:

корни характеристического уравнения:

Переходная характеристика колебательного звена при ступенчатом входном воздействии будет описываться следующим уравнением:

где угловая частота собственных колебаний звена;

 

φ(ω) – аргумент амплитудно-фазовой характеристики звена.

Логарифмические частотные характеристики колебательного звена

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена может быть получена следующим образом:

 

 

Типовое консервативное звено

Можно рассматривать как частный случай ПФ колебательного звена при .

ПФ имеет вид:

Переходная функция :

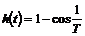
Представляет гармоническую функцию. Колебания продолжаются бесконечное время с постоянной амплитудой (Рис.)

Соответствует системе, в которой отсутствует рассеяние энергии. В механике такие системы называют консервативными.

АФЧХ имеет разрыв на сопрягающей частоте. Резонансный пик равен бесконечности.

ФЧХ скачком изменяется на сопрягающей частоте с нулевого уровня на уровень .

Система, содержащая такое звено, находится на границе устойчивости.

 

---

Дата добавления: 2019-02-22; просмотров: 848; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!