Вращательное движение твердого тела вокруг оси
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие – нибудь две точки, принадлежащие телу (или неизменно связанные с ним), остаются во все время движения неподвижными(рис. 2.2).
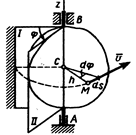
Рисунок 2.2
Проходящая через неподвижные точки А иВпрямая называетсяосью вращения.Так как расстояние между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси будут неподвижны, а все остальные будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направлена осьAz, полуплоскостьІ– неподвижную и полуплоскостьІІврезанную в само тело и вращающуюся вместе с ним. Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком угломφ между этими плоскостями, который назовемуглом поворота тела. Будем считать уголφ положительным, если он отложенот неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца осиAz), а отрицательным, если по ходу часовой стрелки. Измерять уголφбудем в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость углаφот времениt, т.е.
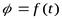 . .
| (25) |
Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорениеε .
Угловая скорость
Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью.
Если за промежуток времени 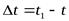 тело совершает поворот на угол
тело совершает поворот на угол 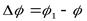 , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет  . В пределе при
. В пределе при 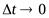 получим
получим
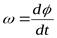 или или 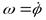 . .
| (26) |
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени.
Правило знаков: когда вращение происходит против хода часовой стрелки, ω >0, а когда по ходу часовой стрелки, тоω <0.
В качестве единицы измерения обычно применяют 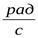 или, так как радиан – величина безразмерная,
или, так как радиан – величина безразмерная, 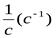 .
.
В теоретических выкладках удобнее пользоваться вектором угловой скорости 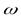 , модуль которого равен
, модуль которого равен 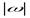 и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно против хода часовой стрелки. Этот вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно против хода часовой стрелки. Этот вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Угловое ускорение
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Если за промежуток времени 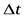 приращение угловой скорости равно
приращение угловой скорости равно  , то отношение
, то отношение 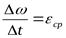 , т.е. определяет значение среднего ускорения вращающегося тела за время
, т.е. определяет значение среднего ускорения вращающегося тела за время 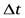 .
.
При стремлении  получаем величину углового ускорения в моментt:
получаем величину углового ускорения в моментt:
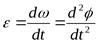 или или  . .
| (27) |
Таким образом, числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела во времени.
В качестве единицы измерения обычно применяют 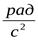 или, что тоже,
или, что тоже, 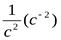 .
.
Дата добавления: 2019-02-22; просмотров: 222; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
