Аналитические формулы для моментов силы относительно координатной оси.
Зависимость между моментами силы относительно центра и относительно оси. Пусть на тело действует приложенная в точке А сила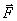 
(рис. 33). Проведем какую-нибудь осьz и возьмем на ней произвольную точку О. Момент силы 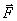относительно центраО будет изображаться вектором 
перпендикулярным плоскости ОАВ, причем по модулю 
.
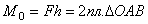Проведем теперь через любую точку O1 на оси z плоскость ху, перпендикулярную к оси; проектируя силу 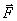на эту плоскость, найдем 
. Но треугольник О1А1В1 представляет собою проекцию треугольника ОАВ на плоскость ху. Угол между плоскостями этих треугольников равен углу между перпендикулярами к плоскостям, т. е. равен 
. Тогда, по известной геометрической формуле, 
Умножая обе части этого равенства на 2 и замечая, что удвоенные пощади треугольниковО1А1В1 и ОАВ равны соответственно mz( 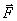) и , найдем окончательно: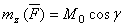 
Так как произведение 
дает проекцию вектора 
на ось z, то равенство можно еще представить в виде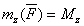 
или 
.В результате мы доказали, что между моментом силы относительно оси и ее моментом относительно какого-нибудь центра, лежащего на этой оси, существует следующая зависимость: момент силы 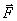относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.
Момент пары сил как вектор.Действие пары сил на тело характеризуется: 1) величиной модуля момента пары, 2) плоскостью действия, 3) направлением поворота в этой плоскости. При рассмотрении пар, не лежащих в одной плоскости, для характеристики каждой из пар необходимо будет задать все эти три элемента. Это можно сделать, если условиться, по аналогии с моментом силы, изображать момент пары соответствующим образом, построенным вектором, а именно: будем изображать момент пары вектором т илиМ, модуль которого равен (в выбранном масштабе) модулю момента пары, т.е. произведению одной из ее сил на плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки (рис. 30).
|
|
|
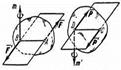
Как известно модуль момента пары равен моменту одной из ее сил относительно точки, где приложена другая сила, т. е. 
; по направлению же векторы этих моментов совпадают. Следовательно 
Равновесие произвольной пространственной системы сил.
На основании основной теоремы статики сформулируем условия равновесия пространственной системы сил.
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор системы сил /? и главный момент М0относительно любого центра были равны нулю
где О — любой центр, т. к. при R = 0 значение М0 от выбора центра не зависит.
|
|
|
Условия равновесия в аналитической форме
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на три координатные оси и сумма моментов всех сил относительно этих осей были равны нулю.
Условия равновесия системы параллельных сил
Рис. 1.32
Для равновесия системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную линиям действия сил, и сумма моментов всех сил относительно двух других осей равнялись нулю (рис. 1.32).
Теорема Вариньона
Рис. 1.33 п
Используя основную теорему статики, докажем теорему Вариньона о моменте равнодействующей. Если заданная система сил имеет равнодействующую, то момент равнодействующей относительного любого центра О равен сумме моментов сил системы относительно
Пусть система сил приводится к равнодействующей R, проходящей через точку С. Приложим в точке С уравновешивающую R' = -R (рис. 1.33).
Тогда система сил F],F1,...,F„,R' должна находиться в равновесии и для нее выполняется условие А/„ = 0, т. е.
Центр параллельных сил.
Центром параллельных сил точки на линии действия равнодействующей этих сил которая не изменяет своего положения при повороте всех сил вокруг их точек приложения на один и тот же угол в одном и том же направлении, точку О приложения равнодействующей системы 2-х параллельных сил является их центральное положение этой точки установлен следующим образом применим теоремы Вариньона о моменте равнодействующих сил для случая сложения 2-х параллельных сил не составил пару сил.
|
|
|
Кинематика
Кинематика точки.
Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.
Дата добавления: 2019-02-22; просмотров: 474; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!