Реакция шероховатых связей. Закон трения.

⇐ ПредыдущаяСтр 6 из 25Следующая ⇒

Если поверхность считается шероховатой, то надо учитывать силу трения. Т.е. шероховатая связь будет слагаться из двух составляющих: из нормальной реакции и перпендикулярной к ней силы трения . Поэтому полная реакция будет отклонена от нормали и поверхности на некоторый угол (рис. 6.1).

Рис. 6.1

При изменении силы трения от нуля до сила 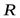будет меняться от до , а ее угол с нормалью будет расти от нуля до некоторого предельного значения . Наибольший угол , который образует полная реакция шероховатой связи с нормалью с поверхностью называется углом трения. Из чертежа видно, что

Так как , то отсюда находим следующую связь между углом трения и коэффициентом трения

Момент силы относительно оси.

Момент силы относительно оси, например O_z (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F’) относительно точки пересечения оси с плоскостью, т.е.

M_z (F) = M_O(F’) = F’∙ h’. (1.9)

Момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например M_z (P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, M_z (Q).

Момент силы относительно оси – скалярная величина.

Рисунок 1.18

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.

Вычисление главного вектора и главного момента системы сил.

Системой сил {F}={F1F2F3...Fn} (Рис.4).называется множество сил, приложенных к точкам механической системы.

Главным вектором системы сил называется векторная сумма всех сил системы: V=Fk (6)

Найти главный вектор можно, построив в произвольном центре О векторный многоугольник, в котором начало последующей силы совпадает с концом предыдущей (рис.4). Замыкающая сторона многоугольника и есть главный вектор V системы сил.

Рис.4

Для пространственной системы сил построить многоугольник практически трудно. Проще найти главный вектор аналитически. Проектируя слагаемые формулу (6) на оси координат, определим проекции главного вектора, его модуль и направляющие косинусы:

Vx=Fkx; Vy=Fky; Vz=Fkz (7)

V2=Vx2+Vy2+Vz2; Cos(V,x)=Vx/V; Cos(V,y)=Vy/V; Cos(V,z)=Vz/V

Момент силы относительно точки. Теоремы о моменте

Пусть сила F приложена в точке А тела, имеющей радиус-вектор r относительно центра О.

Моментом силы F относительно центра О называется вектор

Рис.5

mo(F)=rxF (8)

Направление векторного произведения условно и зависит от ориентированности пространства. Ориентированность пространства- это принятое нами правило соответствия прямой и дуговой стрелок: правого или левого винта. Вектора, направление которых зависит от оринтированности пространства, называются аксиальными. Важно, что для них (Рис.5) дуговая стрелка составляет физическую сущность (показывает направление вращения) а направление самого вектора условено.

Мы будем работать в право ориентированном пространстве и направление векторного произведения всегда будем определять по правилу правого винта: с конца mo видно , что сила стремится повернуть тело против часовой стрелки.

Модуль момента равен произведению модуля силы на плечо h -длину перпендикуляра, опущенного из центра О на линию действия силы.

mo(F)=FrSin=FrSin=Fh (9)

Очевидно, что момент силы тем меньше, чем меньше ее плечо, и он обращается в ноль для любого центра на линии действия силы. Вы это ощущаете, поднимая воротом ведро из колодца, и поэтому стараетесь приложить силу руки так, чтобы создать большее плечо. Из формулы для модуля момента ясно, что момент силы равен нулю только относительно точки, лежащей на линии действия силы.

Теорема 1. О зависимости момента от центра

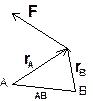
Рис.6 а) в общем случае момент силы зависит от центра б) перенос центра параллельно линии действия силы не изменяет момента

Найдем связь между моментами силы F относительно центров А и В. Из Рис.6 ясно, что

rA= AB+rB mA(F)=rAxF=(AB+rB)xF= rBxF +ABxF

Таким образом

mA(F)= mB(F)+ABxF (10)

Теорема 2. О проекциях моментов.

Проектируя (10) на ось z, проходящую через А и В, находим

Рис.7

Таким образом приходим к лемме: прАВmA(F)=прАВmB(F) (11)

поскольку произведение АВ Х F перпендикулярно АВ и его проекция на z равна нулю. Проекции моментов силы относительно всех точек одной оси на эту ось равны между собой. Таким образом проекция моментов на ось характеризует действие силы по отношению к этой оси, поэтому называется моментом сил относительно. Матричное вычисление векторного произведения (момента). Присоединенная матрица. Известно, что векторное произведение можно представить в виде определителя матрицы

c=a x b

c=a x b == (aFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k (12)

mo(F)=r x F== (yFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k

Здесь i, j, k - орты осей x, y, z с началом в центре О, x, y, z - проекции радиуса-вектора r на эти оси.

В матричной алгебре вектору соответствует столбец его проекций на декартовы оси.

Таким образом вектор-столбец момента имеет вид

mo(F)= (13)

Легко убедится, что этот же результат можно получить, умножив кососимметричную матрицу, составленную из элементов столбца r

R= (14)

на вектор-столбец сил F (1).

m0(F)=RF (15)

Матрица R называется присоединенной матрицей вектора r

В общем случае столбец проекций векторного произведения c=a b удобно находить через присоединенную кососимметричную матрицу первого сомножителя часовой стрелки

c=Ab (16)

Дата добавления: 2019-02-22; просмотров: 324; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!