Определение скорости точки при координатном способе задания движения.

Вектор скорости точки , учитывая, что r_x = x, r_y = y, r_z = z, найдем:

Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам

Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, которая нам наперед известна.

Определение ускорения точки при координатном способе задания движения

Вектор ускорения точки в проекции на оси получаем:

, ,

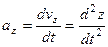
Или , , ,

т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

;

, , ,

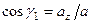где , , - углы, образуемые вектором ускорения с координатными осями.

Касательное и нормальное ускорение точки.

Касательное ускорение точки равно первой производной от модуля скорости или второй производной от расстояния по времени. Касательное ускорение обозначается – .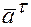

Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости. (рис. 8.5.)

Рис. 8.5

Нормальным ускорением точки называется величина, равная квадрату скорости, деленному на радиус кривизны.

Вектор нормального ускорения направлен от данной точки к центру кривизны, (рис.8.6.). Нормальное ускорение обозначается .

– нормаль к данной точке на траектории движения.

Рис. 8.6.

Полное ускорение точки определяется из векторного уравнения:

Рис. 8.7

Зная направление и модули и 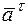, по правилу параллелограмма определим ускорение, соответствующее данной точке траектории движения. Тогда модуль ускорения определим:

8 Поступательное движение твердого тела.

Поступательным называется такое движение твердого тела, при котором любая прямая, неизменно связанная с этим телом, остается параллельной своему начальному положению.

Теорема. При поступательном движении твердого тела все его точки описывают одинаковые траектории и в каждый данный момент имеют равные по модулю и направлению скорости и ускорения.

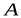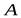Доказательство. Проведем через две точки и , поступательно движущегося тела отрезок и рассмотрим движение этого отрезка в положении . При этом точка описывает траекторию , а точка – траекторию (рис. 56).

Учитывая, что отрезок перемещается параллельно самому себе, и длина его не меняется, можно установить, что траектории точек и будут одинаковы. Значит, первая часть теоремы доказана. Будем определять положение точек и векторным способом относительно неподвижного начала координат 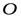. При этом эти радиусы – вектора находятся в зависимости . Так как. ни длина, ни направление отрезка 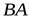не меняется при движении тела, то вектор . Переходим к определению скоростей по зависимости (24):

, получаем .

Переходим к определению ускорений по зависимости (26):

, получаем .

Из доказанной теоремы следует, что поступательное движение тела будет вполне определено, если известно движение только одной какой- нибудь точки. Поэтому изучение поступательного движения твердого тела сводится к изучению движения одной его точки, т.е. к задаче кинематики точки.

Дата добавления: 2019-02-22; просмотров: 348; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!