Приведение системы сил к данному центру.

Систему сил, действующую на твердое тело, можно перенести в одну точку. Эту точку будем называть центром приведения.

При этом сила 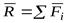,равная геометрической сумме всех сил системы, называетсяглавным вектором системы, а величина 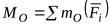, равная сумме моментов всех сил системы относительно центра приведенияO, называется главным моментом системы относительно центра O.

Теорема: Всякая плоская система сил, при приведении к произвольному центру O заменяется одной силой R, равной главному вектору системы, и приложенной в центре приведения, и одной парой с моментом M_O, равным главному моменту системы относительно центра O.

15 Условия равновесия системы сил.

Любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R = 0, M_O= 0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

∑x_i =0, ∑M_ix=0; ∑y_i =0, ∑M_iy=0; (1.20)

∑z_i =0, ∑M_iz=0.

Теорема о моменте равнодействующей.

Момент равнодействующей пространственной системы сходящихся сил относительно произвольной точки равен векторной сумме моментов всех слагаемых сил относительно этой же точки.

Алгебраические моменты силы.

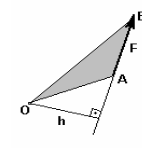
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис.10). Плечом hсилы Fназывают кратчайшее расстояние между этой точкой и линией действия силы. Знак зависит от направления "вращения" тела относительно точки: при "вращении" тела против часовой стрелки будем считать момент положительным М_О - (+) и наоборот М_О - (-).

;

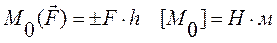
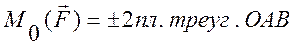
Алгебраические моменты пары.

Векторный момент пары сил, лежащих в плоскости Oxy, также направлен вдоль оси Oz, поскольку он равен векторному моменту одной из сил относительно точки приложения другой силы. Поэтому момент пары сил в этом случае также можно рассматривать как алгебраическую величину.

Алгебраический момент пары сил равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары: M = ±F·d.

Правило знаков моментов пар сил аналогично правилу для моментов сил.

Для показанных на рисунке пар сил (P,P') и (Q,Q') их моменты имеют противоположные знаки: M₁=P·d₁; M₂=-Q·d₂. Поскольку действие пары сил на тело полностью характеризуется ее моментом, на рисунках пару сил принято изображать дуговой стрелкой, показывающей направление действия момента.

Дата добавления: 2019-02-22; просмотров: 488; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!