Момент силы относительно центра.

Момент силы относительно центра О есть вектор , приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр О и силу , в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 2.3а).

Момент силы относительно центра О равен векторному произведению радиуса-вектора, проведенного из центра О в точку А, где приложена сила, на саму силу:

.

Момент силы относительно центра О характеризуется:

1) положением в пространстве плоскости ОАВ (плоскости поворота), проходящей через центр О и силу ;

2) направлением поворота;

3) модулем момента силы.

Модуль момента силы определяется по правилу умножения векторов: модуль векторного произведения двух векторов равен произведению модулей этих векторов на синус угла между ними:

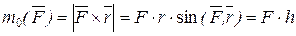, т.к. , где h – кратчайшее расстояние от точки О до линии действия силы - называется плечом силы.

Алгебраическим моментом силы относительно точки называется скалярная величина, равная произведению модуля силы на плече силы относительно этой точки.

Плечом силы относительно точки называется кратчайшее расстояние h от этой точки до линии действия силы. Если сила стремится повернуть тело против хода часовой стрелки, то величина момента силы берётся со знаком «плюс», если по ходу часовой стрелки – знак «минус».

Свойства момента силы: а) момент силы равен нулю, если сила равна нулю или когда плечо равно нулю, т.е. линия действия силы проходит через моментную точку; б) величина момента силы относительно точки не изменяется при переносе силы вдоль линии её действия; в) момент силы численно равен удвоенной площади треугольника, построенного на силе F и полюсе О (рис.2.3б).

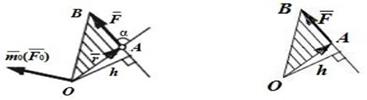
а

б

Рис.2.3

Пл. DOAB = ½ AB·h = ½ F·h. m_o ( ) = Fh = 2·пл DOAB.

Таким образом, алгебраический моменты силы относительно точки О равен: (Н∙м).

Рис. 2.4

Пример. Веревка ВС длиной а, привязанная к столбу под углом α, натягивается с силой, величина которой равна Т (рис. 2.4). Определить момент этой силы относительно точки А.

 

Пара сил.

 

Пара сил - система двух сил, приложенных к телу в двух разных точках: равных по модулю; параллельных; противоположно направленных.

 

Момент пары.

Момент пары сил - произведение модуля любой силы на плечо пары (модуль силы х плечо)

 

12 Свойства пары сил.

1. Сумма проекций на любую ось сил пары равна нулю: F₂cosα – F₁cosα = 0

2. Сумма моментов сил пары относительно любой точки плоскости равна моменту пары.

mom_o( ) = - F₁d = - Fd

mom_o( 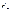) = + F₂l = +Fl

mom_o( ) + mom_o( 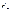) = - Fd + Fl = - F(d-l) = - Fh

Следовательно, пару сил нельзя заменить равнодействующей.

 

Теорема о параллельном переносе силы.

Силу, приложенную к твердому телу, можно, не изменяя оказываемого действия, переносить параллельно ей самой в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

 

---

Дата добавления: 2019-02-22; просмотров: 266; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!