Функции комплексной переменной
7.1. Определение и свойства функции комплексной переменной
Пусть даны две плоскости комплексных чисел и на первой – множество D комплексных чисел z = x + iy, где i – мнимая единица (i2 = –1), на второй – множество G комплексных чисел w = u +iv.
Если каждому числу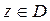 
по некоторому правилу f поставлено в соответствие определенное число 
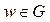, то говорят, что на множестве D задана функция комплексной переменной (ФКП), отображающая множество D в множество G.Обозначается: w = f (z).
Множество D называется областью определения ФКП.
Функцию w = f (z) можно представить в виде
f (z) = u(x,y) + iv(x,y),
где u(x, y) – действительная часть ФКП, v(x, y) – мнимая часть ФКП, обе они – действительные функции от x, y.
Пример 1.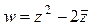 
. Здесь 
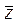= x – iy – число, сопряженное числу z= x + iy.
Выделим действительную и мнимую части ФКП:
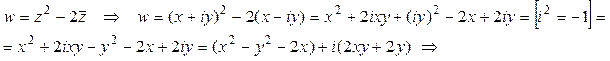u = x2 – y2 – 2x; v = 2xy + 2y.
Вычислим значение функции w в точке z1 = 2 – 3i:
.
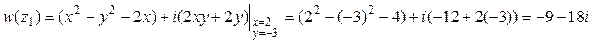Тот же результат получаем непосредственной подстановкой:
.
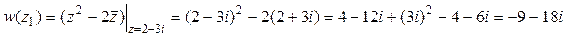Говорят, что ФКП f (z) = u(x,y) +iv(x,y) имеет предел в точке z0, равный числу A = a + ib, если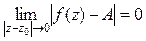 
. Обозначается: 
.
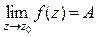Существование предела ФКП w = f (z) при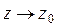 
в означает существование двух пределов: 
.
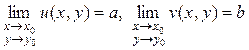ФКП f (z) = u(x,y) +iv(x,y) называется непрерывной в точке z0, если выполняется условие: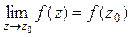 
.
Непрерывность ФКП w = f (z) в точке z0 = x0 + iy0 эквивалентна непрерывности функций u(x, y) и v(x, y) в точке (x0, y0).
Дифференцирование ФКП. Аналитические ФКП
Производной от функции комплексной переменной w = f (z) в точке z0 называется предел:
|
|
|
,
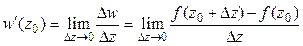где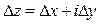 
, и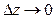 
произвольным образом.
Функцию w = f (z), дифференцируемую в точке z0 и некоторой ее окрестности, называют аналитической,или регулярной функцией в точке z0.
Точки, в которых ФКП не является аналитической, называют особыми точками этой функции.
Для того, чтобы функция f (z) = u(x,y) +iv(x,y) была аналитической в области D необходимо и достаточно, чтобы частные производные 1-го порядка функций u(x, y) и v(x, y) были непрерывны в этой области и выполнялись бы условия:
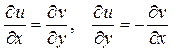, (10)
называемые условиями Эйлера-Даламбера, или условиями Коши-Римана.
Пример 2. Проверить аналитичность ФКП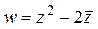 
.
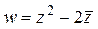Þ u = x2 – y2 – 2x; v = 2xy + 2y (см. пример 1). Проверим выполнение условий Коши-Римана:
.
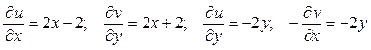Условия (10) не выполняются, следовательно, эта функция не является аналитической.
Пример 3. Проверить аналитичность ФКП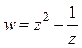 
.
Выделим действительную и мнимую части функции:
.
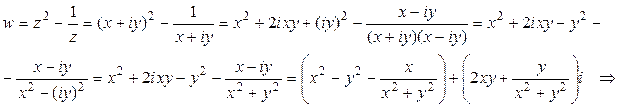
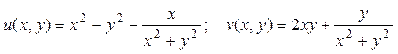Проверим выполнение условий Коши-Римана:
.
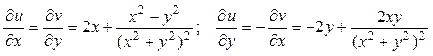Условия выполняются во всех точках, кроме особой точки (0,0), в которой функции и u(x, y) и v(x, y) не определены. Следовательно, функция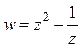 
аналитическая при 
.
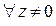Если функция w = f (z) аналитическая в области D, то ее производную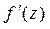 
можно найти, используя правила дифференцирования, аналогичные правилам дифференцирования функции одной действительной переменной.
|
|
|
Пример 4. Вычислить значение производной функции 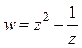в точке
z0 = – 1+ i.
Функция 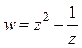– аналитическая, а значит, дифференцируемая во всей своей области определения (см. пример 3). Ее производная:
.
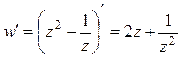Вычислим значение производной в точке z0 = – 1+ i:
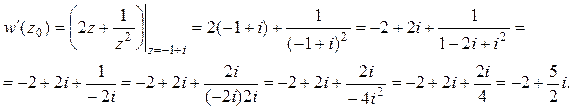
Следовательно,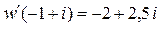 
.
Дата добавления: 2019-02-22; просмотров: 294; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!