Задания для самостоятельной работы
7.11. Найти площади плоских фигур, ограниченных линиями:
а) 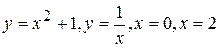 ; ;
| б) 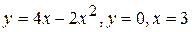 ; ;
|
в)  ; ;
| г) 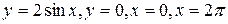 ; ;
|
д) 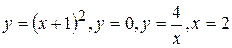 ; ;
| е) 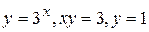 ; ;
|
ж)  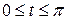 ; ;
| з) 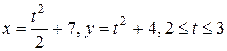 . .
|
7.12. Найти длины дуг кривых, заданных уравнениями:
а)  ; ;
| б) 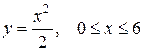 ; ;
|
в) 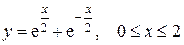 ; ;
| г) 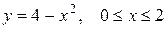 ; ;
|
д) 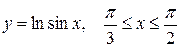 ; ;
| е) 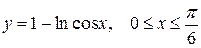 ; ;
|
ж) 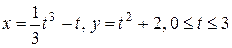 ; ;
| з) 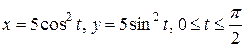 . .
|
7.13. Найти площади поверхностей, образованных вращением вокруг оси  дуг кривых, заданных уравнениями:
дуг кривых, заданных уравнениями:
а) 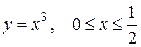 ; ;
| б) 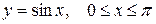 ; ;
|
в) 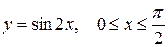 ; ;
| г) 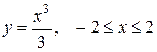 ; ;
|
д)  ; ;
| е) 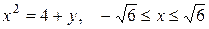 ; ;
|
ж)  ; ;
| з) 
|
7.14. Найти объемы тел, образованных вращением фигур, ограниченных линиями (в заданиях а) – д) ось вращения 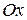 , в заданиях е) – з) ось вращения
, в заданиях е) – з) ось вращения 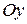 ):
):
а)  ; ;
| б) 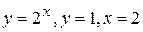 ; ;
|
в) 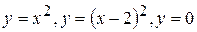 ; ;
| г)  ; ;
|
д)  ; ;
| е) 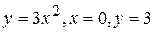 ; ;
|
ж)  ; ;
| з) 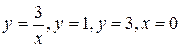 . .
|
Ответы
7.11. а)  ; б)
; б) 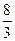 ; в)
; в) 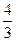 ; г) 8; д)
; г) 8; д) 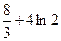 ; е)
; е) 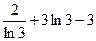 ; ж)
; ж)  ; з)
; з) 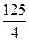 . 7.12. а)
. 7.12. а)  ; б)
; б) 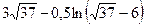 ; в)
; в) 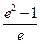 ; г)
; г)  д)
д)  ; е)
; е) 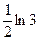 ; ж) 12; з)
; ж) 12; з) 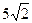 . 7.13. а)
. 7.13. а) 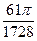 ; б)
; б) 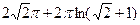 ; в)
; в) 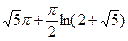 ; г)
; г)  ; д)
; д) 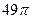 ; е)
; е) 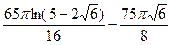 ; ж)
; ж) 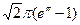 . 7.14. а)
. 7.14. а)  ;б)
;б)  ; в)
; в) 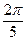 ; г)
; г) 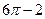 ; д)
; д)  ; е) 1,5; ж)
; е) 1,5; ж) 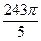 ; з)
; з)  .
.
Приложение определенного интеграла в экономике
Краткие теоретические сведения
Излишек потребителя и излишек производителя
Пусть спрос потребителя на некоторый товар задан функций спроса  , которая представляет собой зависимость оптимальной для потребителя цены товара р от приобретаемого количества товара х. Предположим. Что потребитель потребляет х* единиц товара по цене р*, т.е. платит р*х* рублей. Поскольку, согласно функции спроса, меньшее количество товара потребитель был готов покупать по более высокой цене, возникает излишек потребителя, равный площади фигуры N, изображенной на рис. 15. Излишек потребителя равен сумме, которую надо было бы заплатить потребителю, чтобы заставить его полностью отказаться от приобретения данного товара.
, которая представляет собой зависимость оптимальной для потребителя цены товара р от приобретаемого количества товара х. Предположим. Что потребитель потребляет х* единиц товара по цене р*, т.е. платит р*х* рублей. Поскольку, согласно функции спроса, меньшее количество товара потребитель был готов покупать по более высокой цене, возникает излишек потребителя, равный площади фигуры N, изображенной на рис. 15. Излишек потребителя равен сумме, которую надо было бы заплатить потребителю, чтобы заставить его полностью отказаться от приобретения данного товара.
|
|
|


Пусть функция предложения S(x) показывает, какова должна быть цена товара р, чтобы побудить производителя поставить на рынок х единиц товара. Предположим, что производитель готов продать на рынке х* единиц товара по цене р*. Поскольку, согласно функции предложения, меньшее количество товара производитель был готов поставить по более низкой цене, возникает излишек производителя, равный площади фигуры K, изображенной на рис. 15. Излишек производителя равен разности между минимальной суммой, за которую он был бы готов продать х* единиц товара, и той суммой, за которую он фактически продаёт это количество товара.
Примеры решения типовых задач
Пример 1. Пусть MR(x) – предельный доход фирмы при объёме производства равном х. Дайте экономическую интерпретацию величины
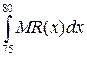 .
.
Решение. Данная величина представляет собой прирост дохода при возрастании объёма производства с х=75 до х=80 единиц.
Пример 2. Фирма планирует увеличить ежедневный объем производства с 10 до 15 единиц. Её текущая функция предельных издержек производства имеет вид MC 1(x)= x2 – 20x + 108. После покупки нового оборудования фирма может поменять функцию предельных издержек на 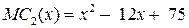 . Вычислите площадь между графиками этих функций предельных издержек от х=10 до х=15. Дайте экономическую интерпретацию полученной величины.
. Вычислите площадь между графиками этих функций предельных издержек от х=10 до х=15. Дайте экономическую интерпретацию полученной величины.
|
|
|
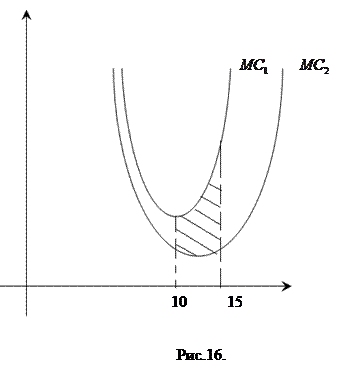

Решение. Графики функций MC 1(x), MC 2(x)представлены на рис. 16.
Искомая площадь S равна
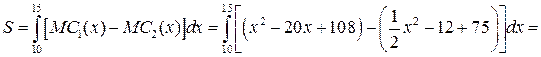
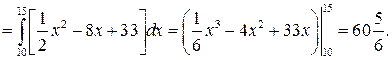
Эта величина представляет собой сумму, на которую будут снижены общие издержки производства в результате использования нового оборудования.
Пример 3. Найдите излишек потребителя в результате реализации 20 единиц товара, если функция спроса имеет вид p = D(x) = 50 – 0,06x2.
Решение. Так как продано 20 единиц товара, то цена реализации должна быть равна
p = 50 – 0,06(20)2 = 26.
Тогда излишек потребителя равен
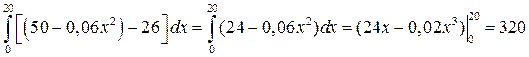
Итак, излишек потребителя составляет 320 денежных единиц.
Пример 4. Пусть деньги поступают на банковский счет непрерывно, при этом итоговая сумма за год составляет 1000 рублей. Данный актив приносит 6% годовых, начисляемых непрерывно в течение года. Определите сумму денег на счете через 5 лет ежегодных вложений при указанных условиях.
Решение. Разделим весь период вложения денег [0, 5] на дневные интервалы Δt = 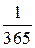 точками t 1 , t 2 , …, tn (здесь t 1=0, а tn=5 – Δt). Так как итоговая сумма за год равна 1000 рублей, то в течение одного дневного интервала времени на счет поступает сумма 1000Δt. Если эта сумма поступила к моменту времени ti, то на неё будут непрерывно начисляться проценты в течение оставшихся (5 – ti) лет. Тогда результатом вложения одной суммы 1000Δt в момент времени ti будет сумма
точками t 1 , t 2 , …, tn (здесь t 1=0, а tn=5 – Δt). Так как итоговая сумма за год равна 1000 рублей, то в течение одного дневного интервала времени на счет поступает сумма 1000Δt. Если эта сумма поступила к моменту времени ti, то на неё будут непрерывно начисляться проценты в течение оставшихся (5 – ti) лет. Тогда результатом вложения одной суммы 1000Δt в момент времени ti будет сумма
|
|
|
 .
.
Сложив результаты ежедневных вложений, получим итоговую сумму
 .
.
Нетрудно заметить, что это сумма Римана для функции на промежутке [0, 5]. Поскольку промежутки времени Δt могут быть сколь угодно малы (так как деньги поступают на счет непрерывно), то переходя к пределу 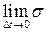 , получим сумму денег на счете через 5 лет хранения при указанных условиях:
, получим сумму денег на счете через 5 лет хранения при указанных условиях:

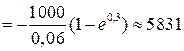 .
.
Таким образом, через 5 лет на счете будет лежать 5831 рубль.
Дата добавления: 2018-10-27; просмотров: 192; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
