Примеры решения типовых задач
Рассмотрим два наиболее простых способа нахождения неопределённых коэффициентов на одном конкретном примере.
Пример 1. Вычислить интеграл 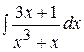 .
.
Решение. I метод – метод неопределённых коэффициентов.
Разложим знаменатель на линейные и квадратичные множители с действительными коэффициентами: 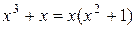 и запишем разложение данной дроби на простейшие с неопределёнными коэффициентами:
и запишем разложение данной дроби на простейшие с неопределёнными коэффициентами: 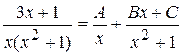 . Приведя к общему знаменателю правую часть, получим равенство числителей:
. Приведя к общему знаменателю правую часть, получим равенство числителей: 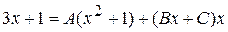 .
.
Приравниваем коэффициенты при одинаковых степенях 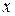 в правой и левой частях этого равенства.
в правой и левой частях этого равенства.
При 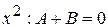 .
.
При 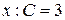 .
.
При 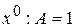 .
.
Тогда 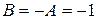 и
и 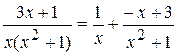 .
.
Далее находим неопределённый интеграл:
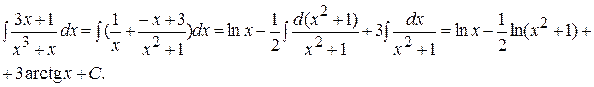
II метод – метод частных значений.
Придадим аргументу 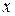 столько различных значений, сколько имеется неопределённых коэффициентов, используя в первую очередь корни знаменателя.
столько различных значений, сколько имеется неопределённых коэффициентов, используя в первую очередь корни знаменателя.
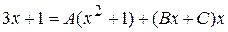 ,
, 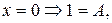

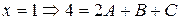 ,
,
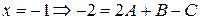 . Тогда получим систему независимых уравнений, из которой имеем:
. Тогда получим систему независимых уравнений, из которой имеем: 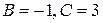 .
.
Пример 2. Вычислить интеграл 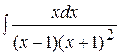 .
.
Решение. Представим дробь в виде суммы простейших дробей с неопределёнными коэффициентами: 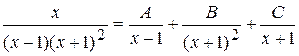 . Приведя дроби в обеих частях к общему знаменателю, получим:
. Приведя дроби в обеих частях к общему знаменателю, получим: 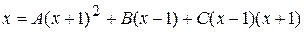 . Найдём неопределённые коэффициенты методом частных значений, придадим аргументу
. Найдём неопределённые коэффициенты методом частных значений, придадим аргументу 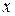 последовательно значения –1, 1, 0. Получим систему:
последовательно значения –1, 1, 0. Получим систему: 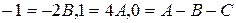 , откуда
, откуда 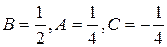 и
и 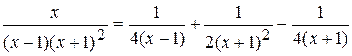 . Таким образом:
. Таким образом: 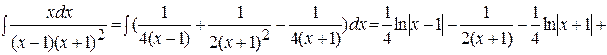
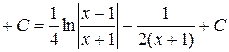 .
.
Пример 3. Вычислить интеграл 
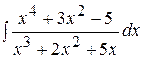 .
.
Решение. Выделим целую часть дроби:
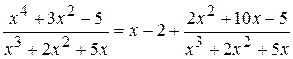 .
.
Разложим знаменатель дроби на множители с действительными коэффициентами:
|
|
|
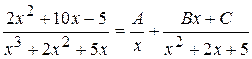 . Умножая это равенство на общий знаменатель, получим:
. Умножая это равенство на общий знаменатель, получим: 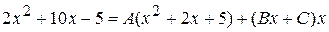 . Приравняем коэффициенты при одинаковых степенях
. Приравняем коэффициенты при одинаковых степенях 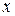 слева и справа.
слева и справа.
При 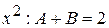 .
.
При 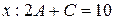 .
.
При 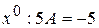 . Тогда
. Тогда 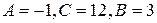 и
и
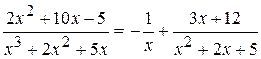 . Итак, вычислим неопределённый интеграл:
. Итак, вычислим неопределённый интеграл: 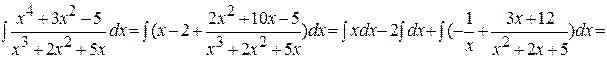
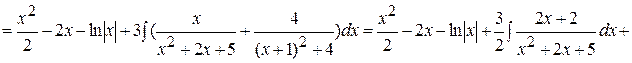
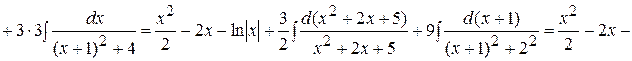
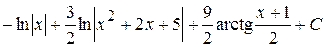 .
.
Задания для самостоятельной работы
7.5. Вычислить интеграл от дроби, содержащий в знаменателе квадратный трехчлен:
а)  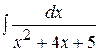  ; ;
| б) 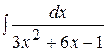 ; ;
|
в) 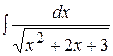 ; ;
| г) 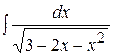 ; ;
|
д) 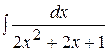 ; ;
| е) 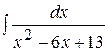 ; ;
|
ж) 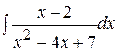 ; ;
| з) 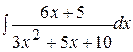 . .
|
7.6. Вычислить интегралы от рациональных функций:
а) 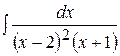 ; ;
| б) 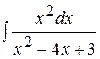 ; ;
|
в) 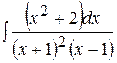 ; ;
| г) 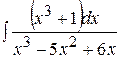 ; ;
|
д) 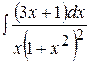 ; ;
| е) 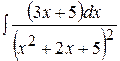 ; ;
|
ж) 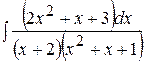
| з) 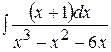 . .
|
Ответы
7.5 a) arctg (x+2)+С; б) 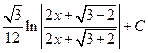 ; в) ln
; в) ln 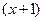 +
+ 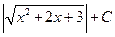 ; г)
; г) 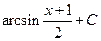 ; д)arctg(2x+1)+С; е)
; д)arctg(2x+1)+С; е) 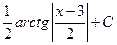 ; ж)
; ж) 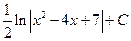 ; з)
; з) 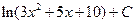 ). 7.6. а)
). 7.6. а) 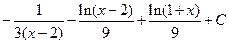 ; б)
; б) 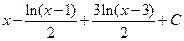 ; в)
; в) 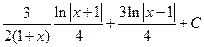 ; г)
; г) 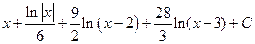 ; д)
; д) 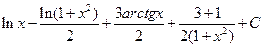 ; е)
; е) 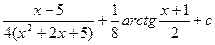 ; ж)3ln(x+2)–
; ж)3ln(x+2)– 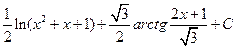 ; з)
; з) 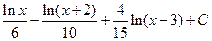
7.3. Интегрирование некоторых тригонометрических и
иррациональных функций
Краткие теоретические сведения
В этом параграфе для интегралов от некоторых классов тригонометрических и иррациональных выражений будут даны рационализирующие подстановки, то есть замены переменной, приводящие исходный интеграл к интегралу от рациональной дроби. Здесь через  будем обозначать рациональные функции.
будем обозначать рациональные функции.
Интегрирование тригонометрических функций
I. Интегралы вида 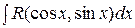 приводятся к интегралам от рациональной функции новой переменной
приводятся к интегралам от рациональной функции новой переменной 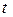 с помощью универсальной тригонометрической подстановки
с помощью универсальной тригонометрической подстановки 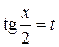 .В этом случае
.В этом случае 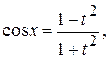
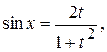
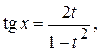
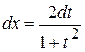 .
.
|
|
|
Подставляя в подынтегральное выражение вместо 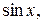
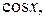
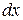 их выражения через
их выражения через 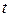 ,
, 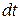 , получим интеграл от рациональной дроби:
, получим интеграл от рациональной дроби:
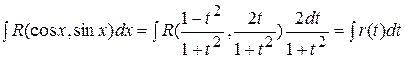 .
.
В случае, когда имеет место тождество
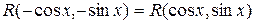 для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку
для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку 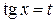 . При этом
. При этом 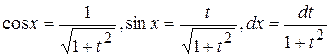 .
.
Если 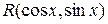 – нечетная функция относительно
– нечетная функция относительно 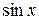 , т.е.
, т.е. 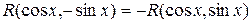 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 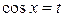 .
.
Если 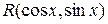 – нечетная функция относительно
– нечетная функция относительно 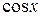 , т.е.
, т.е. 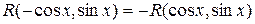 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 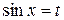 .
.
II. Для отыскания интегралов вида
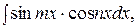
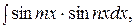
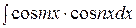 используют следующие формулы:
используют следующие формулы:
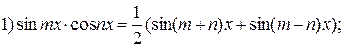
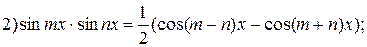
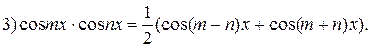
При нахождении интегралов вида 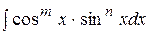
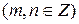 возможны следующие случаи:
возможны следующие случаи:
1) хотя бы одно из чисел 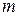 или
или 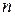 – нечетное, например
– нечетное, например 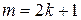 , тогда
, тогда 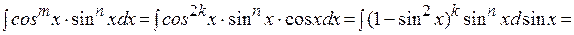
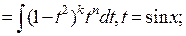
2) оба числа 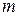 или
или 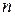 – четные, тогда рекомендуется использовать следующие формулы, позволяющие понизить степень тригонометрических функций:
– четные, тогда рекомендуется использовать следующие формулы, позволяющие понизить степень тригонометрических функций: 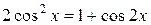 ,
, 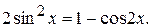
Дата добавления: 2018-10-27; просмотров: 206; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
