Примеры решения типовых задач
Пример 1. 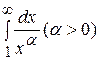 . Установить при каких значениях
. Установить при каких значениях 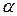 этот интеграл сходится, а при каких расходится.
этот интеграл сходится, а при каких расходится.
Решение. Пусть 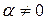 . Тогда
. Тогда 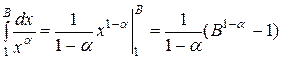 .
.
Итак,  . Следовательно, если
. Следовательно, если 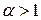 , то
, то 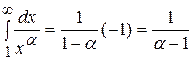 (т.к.
(т.к. 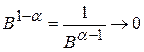 при
при 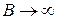 ), т.е. интеграл сходится; если
), т.е. интеграл сходится; если  , то
, то  (т.к.
(т.к.  при
при  ), т.е. интеграл расходится.
), т.е. интеграл расходится.
При 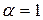
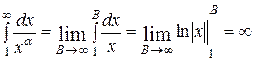 , т.е. интеграл расходится.
, т.е. интеграл расходится.
Пример 2. Доказать, что 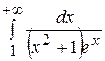 сходится.
сходится.
Решение. Известно, что при 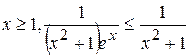 . Тогда
. Тогда 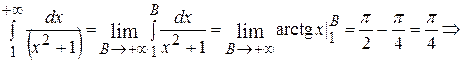
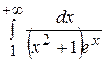 – сходится.
– сходится.
Пример 3. Исследовать на сходимость интеграл 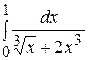 .
.
Решение. Функция терпит разрыв в точке 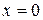 . Очевидно, что при
. Очевидно, что при 
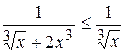 , тогда
, тогда
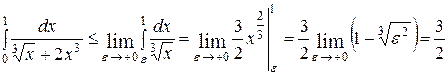 . Итак, интеграл
. Итак, интеграл 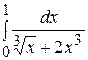 сходится.
сходится.
Пример 4. Исследовать на сходимость интеграл  .
.
Решение. Подынтегральная функция терпит бесконечный разрыв при 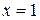 , следовательно, по определению:
, следовательно, по определению:
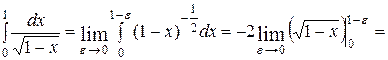
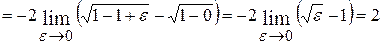 . Интеграл сходится.
. Интеграл сходится.
Пример 5. Найти условия сходимости и расходимости несобственных интегралов 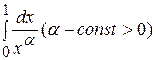 .
.
Решение. Подынтегральная функция терпит бесконечный разрыв при 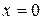 .
.
Пусть 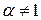 .
.
Тогда 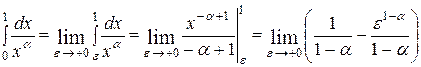 и если
и если 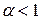 , то
, то  ;если
;если 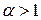 , то
, то 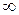 .
.
Пусть 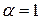 . Тогда
. Тогда
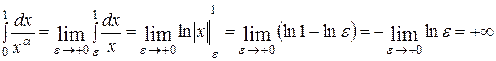 .
.
Итак, данный интеграл сходится при 
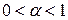 и расходится при
и расходится при  .
.
Задания для самостоятельной работы
7.10. Исследовать на сходимость интегралы:
а) 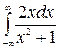 ; ;
| б) 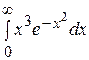 ; ;
|
в) 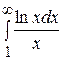 ; ;
| г) 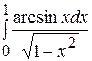 ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  . .
|
Ответы
7.10. а)0; б)  ; в)
; в) 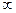 ; г)
; г)  ; д) не существует; е)
; д) не существует; е)  ; ж)2; з)
; ж)2; з)  .
.
Приложения определённого интеграла
Краткие теоретические сведения
Площадь криволинейной трапеции
 Площадь криволинейной трапеции в декартовых координатах
Площадь криволинейной трапеции в декартовых координатах
Нами было установлено, что геометрический смысл определённого интеграла – площадь криволинейной трапеции, ограниченной осью  , прямыми
, прямыми 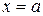 ,
, 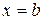 и графиком функции
и графиком функции 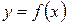 . Таким образом, если функция
. Таким образом, если функция 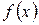 неотрицательна на отрезке
неотрицательна на отрезке 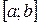 , то площадь
, то площадь 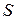 под кривой
под кривой 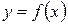 на
на 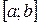 (рис. 4) численно равна определенному интегралу от
(рис. 4) численно равна определенному интегралу от 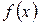 на данном отрезке:
на данном отрезке:
|
|
|
 . (1)
. (1)
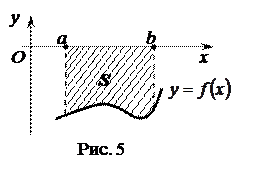 Если функция
Если функция 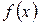 неположительна на отрезке
неположительна на отрезке 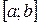 , то площадь
, то площадь 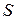 над кривой
над кривой 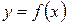 на
на 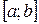 (рис. 5) численно равна определенному интегралу от
(рис. 5) численно равна определенному интегралу от 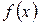 на данном отрезке, взятому со знаком «минус»:
на данном отрезке, взятому со знаком «минус»:
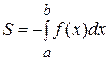 . (2)
. (2)
 Если
Если 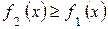 на отрезке
на отрезке 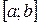 , то
, то 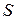 фигуры, заключенной между кривыми
фигуры, заключенной между кривыми 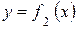 и
и  на этом отрезке (рис.6) вычисляется по формуле
на этом отрезке (рис.6) вычисляется по формуле

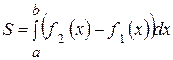 . (3)
. (3)
Если криволинейная трапеция прилегает к оси ординат и ограничена непрерывной кривой 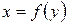 , прямыми
, прямыми  ,
, 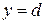 и осью
и осью 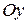 (рис. 7), то ее площадь вычисляется по формуле
(рис. 7), то ее площадь вычисляется по формуле
 . (4)
. (4)
Площадь криволинейной трапеции в случае параметрического
задания граничной кривой
Для вычисления площади криволинейной трапеции при задании верхней ограничивающей кривой параметрическими уравнениями 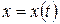 ,
,  , где
, где 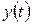 – непрерывна, а
– непрерывна, а  – монотонно возрастает и непрерывно дифференцируема на отрезке
– монотонно возрастает и непрерывно дифференцируема на отрезке 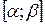 и
и 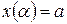 ,
, 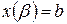 , достаточно в формуле для вычисления площади в прямоугольных декартовых координатах сделать в интеграле замену переменной
, достаточно в формуле для вычисления площади в прямоугольных декартовых координатах сделать в интеграле замену переменной  :
:
|
|
|
 (5)
(5)
При монотонном убывании  , то есть при
, то есть при 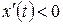 ,
, 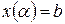 ,
, 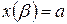 будем иметь
будем иметь
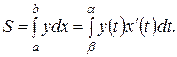 (6)
(6)
Длина дуги кривой
Длина дуги кривой в декартовых координатах
 Пусть
Пусть 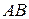 – несамопересекающаяся незамкнутая дуга кривой. Такие дуги называются также простыми дугами. За длину простой дуги принимают предел периметров вписанных ломаных при стремлении наибольшей
– несамопересекающаяся незамкнутая дуга кривой. Такие дуги называются также простыми дугами. За длину простой дуги принимают предел периметров вписанных ломаных при стремлении наибольшей
из длин звеньев ломаной к нулю, если этот предел существует и конечен. В случае замкнутой кривой, а также самопересекающейся кривой, когда она может быть разбита на конечное число простых дуг, за длину кривой принимают сумму длин простых дуг, ее составляющих (рис. 8).
Пусть дуга 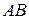 задана уравнением
задана уравнением 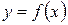 ,
, 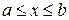 , где функция
, где функция 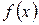 – непрерывна и имеет непрерывную производную на отрезке
– непрерывна и имеет непрерывную производную на отрезке 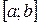 . Тогда ее длина
. Тогда ее длина 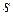 вычисляется по формуле:
вычисляется по формуле:
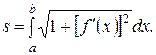 (7.)
(7.)
Дата добавления: 2018-10-27; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
