Длина дуги кривой, заданной параметрическими уравнениями
Пусть дуга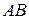 
задана параметрическими уравнениями 
, 
, 
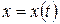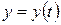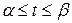, где 
, 
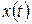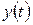– непрерывно дифференцируемые функции на отрезке 
, 
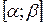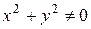и 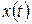– монотонная функция. Тогда длина 
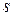дуги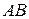 
вычисляется по формуле
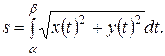(8)
Площадь поверхности вращения
Площадь поверхности вращения в декартовых координатах
Пусть поверхность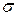 
образована вращением вокруг оси 
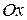дуги 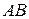, заданной уравнением 
, 
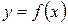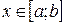, где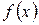 
– неотрицательная непрерывно дифференцируемая на отрезке 
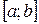функция.
За площадь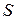 
поверхности вращения 
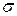принимают предел площадей поверхностей, образованных вращением вокруг оси 
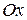вписанных в дугу 
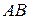ломаных, при неограниченном увеличении числа звеньев ломаной и стремлении к нулю наибольшей из длин ее звеньев.
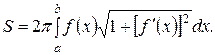(9)
Площадь поверхности вращения в случае параметрического задания кривой
В случае задания кривой 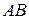параметрическими уравнениями 
, 
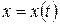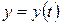, где функции , 
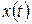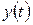– непрерывно дифференцируемые функции на отрезке 
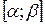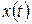, – монотонна и 
, 
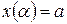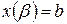, в результате замены переменной 
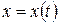в интеграле в равенстве (7.8) получаем формулу
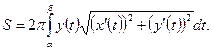(10)
Объём тел вращения
Пусть функция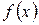 
непрерывна и неотрицательна на 
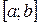. Тогда тело, которое образуется вращением вокруг оси 
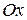криволинейной трапеции, ограниченной сверху графиком функции 
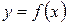(рис. 9), имеет объём
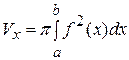. (11)
|
|
|
Если тело вращается вокруг оси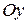 
(рис.10), то его объём:
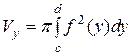. (12)
Примеры решения типовых задач
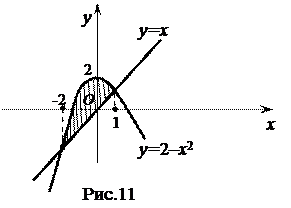Пример 1. Найти площадь фигуры, ограниченной линиями: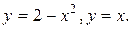 
Решение. Изобразим данную фигуру (рис. 11.).
Площадь заданной фигуры может быть найдена с помощью интеграла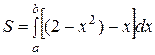 
(формула 3). Найдём границы интегрирования, решив систему уравнений 
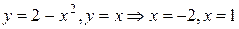, т.е. 
, 
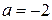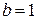. Итак, согласно формуле (7.3), имеем:
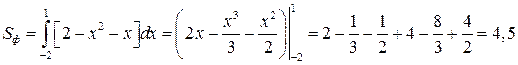(кв.ед.).
Пример 2. Найти площадь фигуры, ограниченной линиям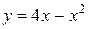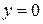и: 
, 
и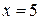 
.
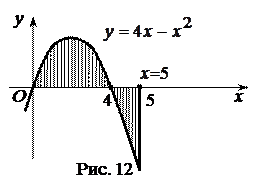Решение. Парабола 
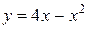пересекает ось абсцисс в точках 
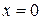и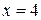 
. Фигура, площадь которой требуется найти показана на рис. 12 штриховкой. Пусть 
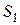и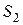 
– площади частей этой фигуры, соответствующих отрезкам 
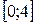и 
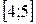, а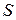 
– искомая площадь; тогда 
.
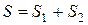Используя формулу (1), получим
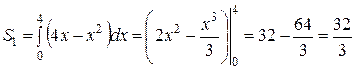(кв. ед.), а по формуле (2) находим 
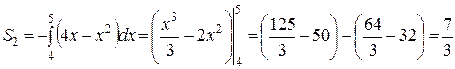(кв. ед.).
Следовательно,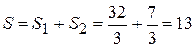 
(кв. ед.).
Пример 3. Найти площадь фигуры, ограниченной одной аркой циклоиды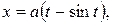 
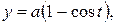
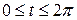и осью 
(рис. 13).
Решение. По формуле (5) имеем
.
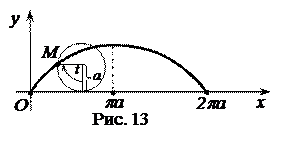
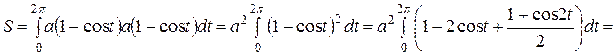
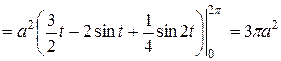Пример 4. Вычислить длину дугипараболы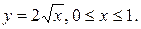 
Решение. Функция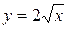 
непрерывна на отрезке 
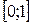, ее производная 
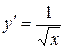непрерывна на полуинтервале 
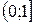и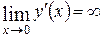 
. Поэтому для длины данной дуги параболы по формуле (7.7.) получаем несобственный интеграл 
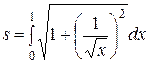. Определение несобственных интегралов было рассмотрено в параграфе 6. Имеем 
.
|
|
|
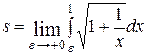Рассмотрим отдельно неопределенный интеграл:
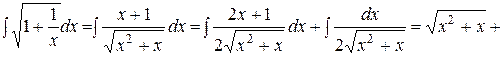
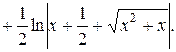Тогда
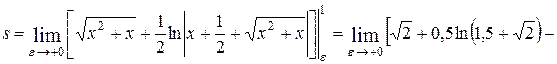
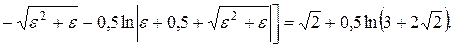
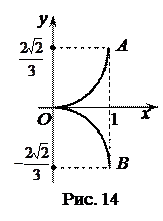Пример 5. Найти длину дуги полукубической параболы 
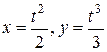, отсеченной прямой 
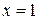(рис. 14).
Решение. Длина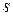 
дуги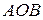 
равна удвоенной длине дуги 
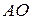. Значение параметра 
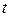, соответствующее точке 
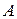пересечения параболы с прямой, найдем из системы уравнений 
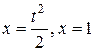. Получим 
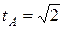. Аналогично 
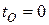. Тогда
.
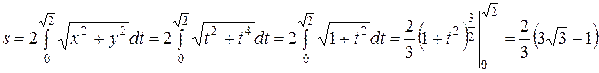Пример 6. Вычислить площадь части поверхности параболоида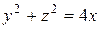 
, отсеченной плоскостью 
.
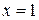Решение. Данная поверхность является поверхностью, образованной вращением вокруг оси 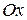дуги параболы 
, 
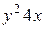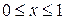. Тогда 
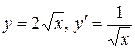и по формуле (7.9.) получаем:
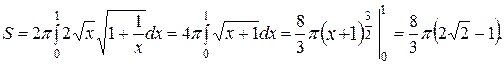
Пример 7. Найти площадь поверхности, полученной вращением циклоиды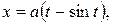 
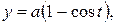
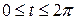вокруг оси 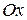(см. рис. 13)
Решение. По формуле (10) имеем
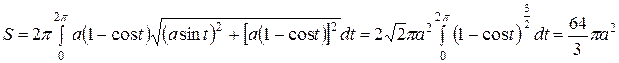Пример 8. Найти объём тела, образованного вращением вокруг оси 
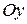фигуры, ограниченной линиями 
.
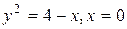Решение. Объём тела найдём, используя формулу (12):
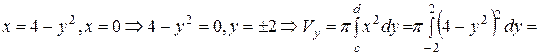
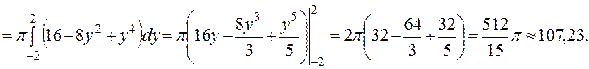
Дата добавления: 2018-10-27; просмотров: 525; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!