Примеры решения типовых задач
Пример 1. Вычислить интеграл 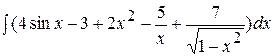 .
.
Решение. Воспользуемся свойствами 3 и 4 и табличными интегралами (5), (2), (3), (9). Получим:
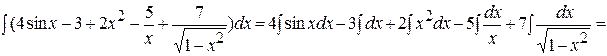
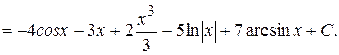
Пример 2. Вычислить интеграл 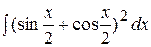 .
.
Решение. Возведём в квадрат подынтегральную функцию, проведём тригонометрические преобразования, применим свойство 4 и табличные интегралы (2),(5)
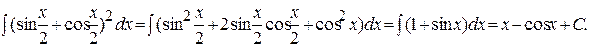
Пример 3. Вычислить интеграл 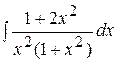 .
.
Решение. Применив тождественные преобразования, свойство 4 и табличные интегралы (2), (10), получим:
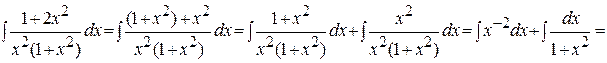
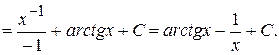
Пример 4. Вычислить интеграл  .
.
Решение. Введём переменную 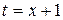 ,
, 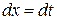 . Тогда
. Тогда 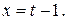 Используем формулу (2.1)
Используем формулу (2.1)
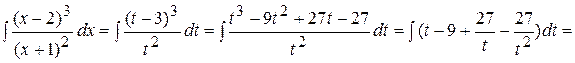
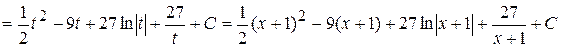 .
.
При замене переменной в неопределённом интеграле иногда более удобно заменять не  как функцию
как функцию 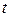 , а наоборот, задавать
, а наоборот, задавать 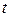 как функцию от
как функцию от  .
.
Пример5. Вычислить интеграл 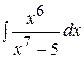 .
.
Решение. Положим 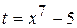 . Тогда
. Тогда 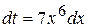 . Используя формулу (2.1) и табличный интеграл (3), получим:
. Используя формулу (2.1) и табличный интеграл (3), получим:
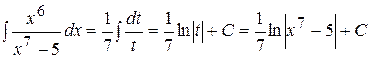 .
.
Пример 6. Вычислить интеграл  .
.
Решение. Применим известное тригонометрическое тождество, далее положим 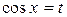 . Тогда
. Тогда 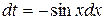 . Используя табличный интеграл (2), имеем:
. Используя табличный интеграл (2), имеем:
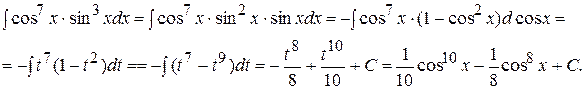 Пример 7. Вычислить интеграл
Пример 7. Вычислить интеграл 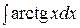 .
.
Решение. Положим  . Тогда
. Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим:
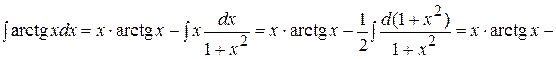
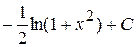 , где
, где 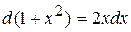 .
.
Пример 8. Вычислить интеграл 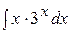 .
.
Решение. Положим 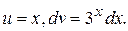 Тогда
Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим:
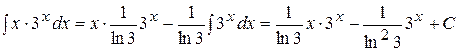 .
.
Пример 9. Вычислить интеграл 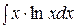 .
.
Решение. Положим 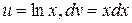 . Тогда
. Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим:
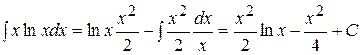 .
.
В некоторых случаях формулу интегрирования по частям приходится применять несколько раз.
|
|
|
Пример 10. Вычислить интеграл 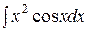 .
.
Решение. Положим  . Тогда
. Тогда 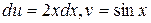 , по формуле интегрирования по частям имеем:
, по формуле интегрирования по частям имеем: 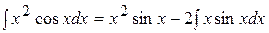 . Далее, пусть
. Далее, пусть 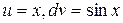 . Тогда
. Тогда 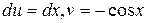 , ещё раз применив формулу интегрирования по частям, имеем:
, ещё раз применив формулу интегрирования по частям, имеем: 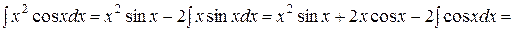
 .
.
Задания для самостоятельной работы
7. 1. Вычислить интегралы с помощью непосредственного интегрирования:
а) 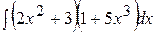 ; ;
| Б) 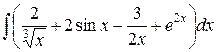 ; ;
|
в) 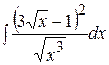 ; ;
| Г) 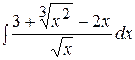 ; ;
|
д) 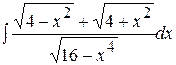 ; ;
| Е) 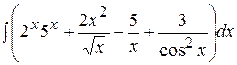 ; ;
|
ж)  ; ;
| З) 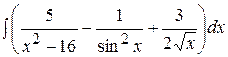 . .
|
7.2. Вычислить интегралы с помощью метода замены переменной:
а) 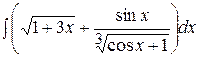 ; ;
| б) 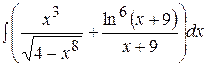 ; ;
|
в)  ; ;
| г) 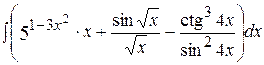 ; ;
|
д) 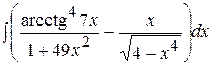 ; ;
| е) 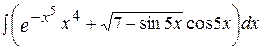 ; ;
|
ж)  ; ;
| з) 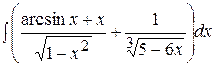 . .
|
7.3. Вычислить интеграл методом интегрирования по частям:
а) 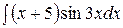 ; ;
| б)  ; ;
|
в) 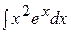 ; ;
| г) 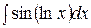 ; ;
|
д) 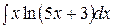 ; ;
| е) 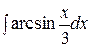 ; ;
|
ж) 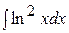 ; ;
| з) 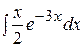 . .
|
7.4. Разные задачи.
а)  ; ;
| б) 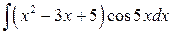 ; ;
|
в) 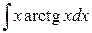 ; ;
| г) 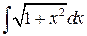 ; ;
|
д) 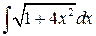 ; ;
| е) 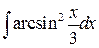 ; ;
|
ж) 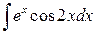 ; ;
| з) 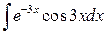 . .
|
Ответы
7.1. а) 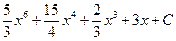 ; б)
; б)  ; в)
; в) 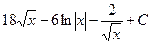 ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж) 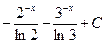 ; з)
; з) 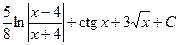 . 7.2. а)
. 7.2. а) 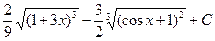 ; б)
; б) 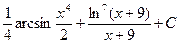 ; в)
; в) 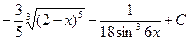 ; г)
; г) 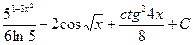 ; д)
; д)  ; е)
; е)  ; ж)
; ж) 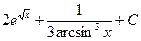 ; з)
; з)  .7.3. а)
.7.3. а)  ; б)
; б) 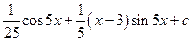 ; в)e
; в)e 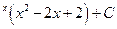 ; г)
; г) 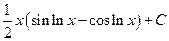 ; д)
; д) 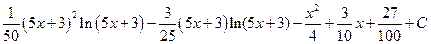 ; е)xarcsin3x+3
; е)xarcsin3x+3 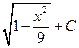 ; ж)
; ж) 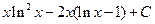 ; з)-
; з)- 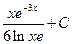 .7.4. a)
.7.4. a) 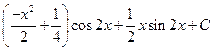 ; б)
; б) 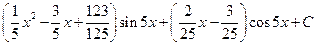 ; в)
; в) 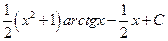 ; г)
; г) 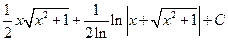 ; д)
; д) 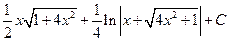 ; ж)
; ж) 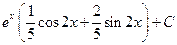 ; з)e
; з)e 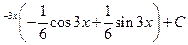 .
.
Интегрирование рациональных функций
Краткие теоретические сведения
Рациональными функциями называются функции вида: 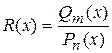 , где
, где 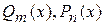 – многочлены степени
– многочлены степени  соответственно.
соответственно.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае называется неправильной. Всякую неправильную рациональную дробь можно, деля числитель на знаменатель, представить в виде суммы многочлена, называемого целой частью дроби, и правильной рациональной дроби.
|
|
|
Например:  .
.
Будем рассматривать правильные рациональные дроби с действительными коэффициентами многочленов в числителе и знаменателе. Среди них назовём простейшими дроби вида: 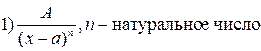 ,
, 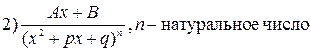 .
.
Теорема (о разложении правильной дроби в сумму простейших дробей). Всякую рациональную правильную дробь со знаменателем представимым в виде произведения можно разложить в виде суммы простейших рациональных дробей вида 1 – 2. В этом разложении каждому корню  кратности
кратности 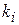 многочлена
многочлена 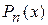 соответствует сумма k дробей вида
соответствует сумма k дробей вида 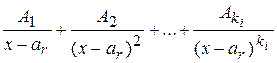 , где
, где 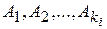 – действительные числа, называемые неопределёнными коэффициентами.
– действительные числа, называемые неопределёнными коэффициентами.
Дата добавления: 2018-10-27; просмотров: 192; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
