Интегрирование некоторых иррациональных функций
Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определённых подстановок приводятся к интегралам от рациональных функций новой переменной.
I. Интеграл вида  , где
, где 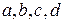 – постоянные,
– постоянные,  приводятся к интегралу от рациональной функции новой переменной
приводятся к интегралу от рациональной функции новой переменной  с помощью подстановки
с помощью подстановки  , где
, где  наименьшее общее кратное (НОК) знаменателей дробей
наименьшее общее кратное (НОК) знаменателей дробей  , т.е.
, т.е.  .
.
II. Интегралы вида


 тригонометрическими подстановками соответственно
тригонометрическими подстановками соответственно 

 сводятся к уже рассмотренным интегралам вида
сводятся к уже рассмотренным интегралам вида  .
.
К рассмотренным интегралам могут быть преобразованы интегралы  , если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной. Существуют и другие методы интегрирования указанного интеграла, мы их здесь не рассматриваем.
, если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной. Существуют и другие методы интегрирования указанного интеграла, мы их здесь не рассматриваем.
Примеры решения типовых задач
Пример 1. Вычислить интеграл 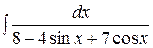 .
.
Решение: Воспользуемся универсальной тригонометрической подстановкой:
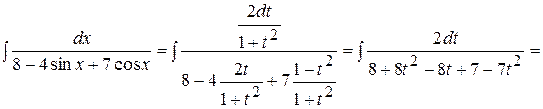

Пример 2. Вычислить интеграл  .
.
Решение. Используем замену переменной  . Тогда
. Тогда  ,
,  . Получаем:
. Получаем:
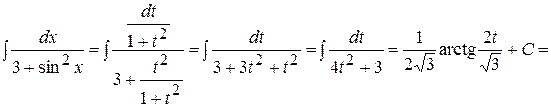
 .
.
Пример 3. Вычислить интеграл 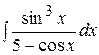 .
.
Решение. Данная функция нечетна относительно  . Используем замену переменной
. Используем замену переменной  . Тогда
. Тогда 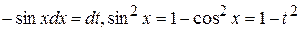 и
и


Пример 4. Вычислить интеграл  .
.
Решение. Применив формулу (1) и табличные интегралы, получим:


Пример 5. Вычислить интеграл 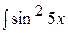 .
.
Решение. Воспользуемся формулой  .
.  .
.
|
|
|
Пример 6. Вычислить интеграл  .
.
Решение. Так как  , то положим
, то положим  . Тогда
. Тогда 
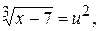

 и
и 



Пример 7. Вычислить интеграл  .
.
Решение. Положим  . Тогда
. Тогда 
 и исходный интеграл преобразуется в интеграл вида
и исходный интеграл преобразуется в интеграл вида  . Интегрируя его, получим:
. Интегрируя его, получим: 
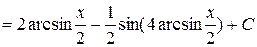 .
.
Задания для самостоятельной работы
7.7. Вычислить интегралы от тригонометрических функций:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 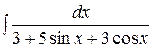 ; ;
|
д)  ; ;
| е)  ; ;
|
ж)  ; ;
| з)  . .
|
7.8. Вычислить интегралы от иррациональных функций:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  : :
|
д) 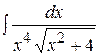 ; ;
| е) 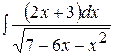 ; ;
|
ж)  ; ;
| з)  . .
|
Ответы
7.7 . а)  ; б)
; б)  ; в)
; в) 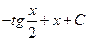 ;
;  г)
г)  ln (6+10 arctg
ln (6+10 arctg 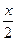 )+ С; д)–
)+ С; д)–  ln
ln  +
+  ; е)
; е)  ; ж) lntg
; ж) lntg  ; з)3x+4sin2x+С. 7.8. а)
; з)3x+4sin2x+С. 7.8. а)  ; б)
; б)  ; г)arcsin
; г)arcsin  +С; д)
+С; д) 
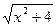 + С; е)–2
+ С; е)–2  –-3arcsin
–-3arcsin  +С; ж)
+С; ж)  –arcsin
–arcsin 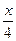 +С; з)
+С; з)  .
.
Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла
Краткие теоретические сведения
Пусть функция  определена на
определена на  . Разобьём
. Разобьём  произвольным образом точками
произвольным образом точками  на
на  частичных отрезков длиной
частичных отрезков длиной  . Выберем в каждой из них точку
. Выберем в каждой из них точку  и найдем значения функции в каждой из этих точек
и найдем значения функции в каждой из этих точек 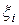 –
–  . Сумма вида
. Сумма вида
 (1)
(1)
называется n-ой интегральной суммой функции  на
на  .
.
 Геометрический смысл интегральной суммы (1) – сумма площадей прямоугольников с основаниями
Геометрический смысл интегральной суммы (1) – сумма площадей прямоугольников с основаниями 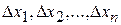 и высотами
и высотами  . Обозначим через
. Обозначим через  длину наибольшего частичного отрезка данного разбиения
длину наибольшего частичного отрезка данного разбиения  (рис.1).
(рис.1).
|
|
|
Определение. Если существует конечный предел  суммы (5.1) при
суммы (5.1) при 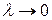 , то этот предел называется определённым интегралом от функции
, то этот предел называется определённым интегралом от функции 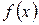 по отрезку
по отрезку  и обозначается:
и обозначается:  .
.
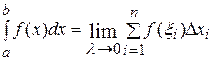 ,
,
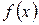 – подынтегральная функция,
– подынтегральная функция,  – подынтегральное выражение,
– подынтегральное выражение,  – отрезок интегрирования,
– отрезок интегрирования,  и
и  – нижний и верхний пределы интегрирования,
– нижний и верхний пределы интегрирования,  – переменная интегрирования.
– переменная интегрирования.
Теорема. Если функция  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  , т.е. предел интегральной суммы (1) существует и не зависит от способа разбиения
, т.е. предел интегральной суммы (1) существует и не зависит от способа разбиения  на частичные отрезки
на частичные отрезки  и выбора на них точек
и выбора на них точек 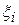 .
.
Если  , то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции
, то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции  , осью
, осью  и прямыми
и прямыми 
 . Эта фигура – криволинейная трапеция. В общем случае, когда функция
. Эта фигура – криволинейная трапеция. В общем случае, когда функция  на
на  принимает значения разных знаков, определённый интеграл выражает разность площадей криволинейных трапеций, расположенных над осью
принимает значения разных знаков, определённый интеграл выражает разность площадей криволинейных трапеций, расположенных над осью  и под ней, т.к.
и под ней, т.к.  расположенной под осью
расположенной под осью  , присваивается знак «–».
, присваивается знак «–».
Далее будем рассматривать функцию 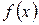 непрерывную на
непрерывную на  . По определению полагают, что определённый интеграл от функции с равными верхним и нижним пределами интегрирования равен нулю
. По определению полагают, что определённый интеграл от функции с равными верхним и нижним пределами интегрирования равен нулю
 . (2)
. (2)
|
|
|
1. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный
 . (3)
. (3)
2. Каковы бы ни были числа  имеет место равенство
имеет место равенство
 . (4)
. (4)
Определённый интеграл по всему отрезку равен сумме интегралов по его частям (аддитивность по области интегрирования).
3. Постоянный множитель можно вынести за знак определённого интеграла, т.е.
 . (5)
. (5)
4. Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
 . (6)
. (6)
Свойства 3,4 называются свойствами линейности.
Далее будем считать, что  .
.
5. Если всюду на 
 , то
, то  .
.
6. Монотонность. Если всюду на 
 , то
, то  .
.
7. Оценка модуля интеграла. Если функция 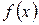 непрерывна на
непрерывна на  , то
, то
 . (7)
. (7)
Следствие.Если всюду на 
 , то
, то 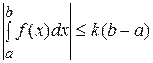 .
.
8. Если  и
и  – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 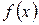 на
на  , то
, то
 . (8)
. (8)
9. Теорема о среднем. Если 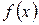 непрерывна на
непрерывна на  , то на этом отрезке существует точка
, то на этом отрезке существует точка  , что
, что
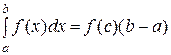 . (9)
. (9)
10. Интеграл с переменным верхним пределом. Если функция  непрерывна и
непрерывна и  , то имеет место равенство
, то имеет место равенство  , т.е. производная определённого интеграла по переменному верхнему пределу
, т.е. производная определённого интеграла по переменному верхнему пределу  равна значению подынтегральной функции при том же
равна значению подынтегральной функции при том же  – первообразная для функции
– первообразная для функции 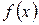 .
.
|
|
|
11. Формула Ньютона-Лейбница. Если  – первообразная функции
– первообразная функции  , непрерывной на
, непрерывной на  , то
, то
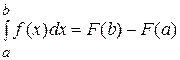 . (10)
. (10)
Формула (10) даёт простой метод вычисления определённого интеграла: определённый интеграл от непрерывной функции равен разности значений любой её первообразной, вычисленных для верхнего и нижнего пределов интегрирования. Таким образом, задача вычисления определённого интеграла сводится к задаче вычисления неопределённого интеграла, которая достаточно изучена. Здесь используются те же методы интегрирования.
Дата добавления: 2018-10-27; просмотров: 288; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
