Кинематический анализ механизма с группами Ассура 2-го класса

Го и 5-го вида

Задан кулисный механизм, показанный на рис. 4.5.

Кривошип 1, вращаясь с заданной постоянной угловой скоростью ω₁ вокруг точки О, перемещает камень 2. Камень заставляет кулису 3 качаться относительно точки А. Точка С кулисы, действуя на ползун 4, поступательно перемещает выходное звено 5 по неподвижным направляющим х-х.

Даны: длины всех звеньев в метрах: l_OA; l_AB; l _АС ; расстояния между точками А, О и направляющей  х-х стойки.

Требуется: построить планы скоростей и ускорений для данного положения механизма, определить величины и направления скоростей и ускорений всех точек, указанных на механизме, а также угловые скорости и угловые ускорения звеньев.

План механизма, выполненный в масштабе μ_S, показан на рис. 4.5.

Механизм состоит из двух групп Ассура 2-го класса 3-го и 5-го видов и механизма 1-го класса.

 

 

Рис. 4.5. Структурный и кинематический анализ кулисного механизма

 

Скорости точек B₁ и В₂ , принадлежащих соответственно кривошипу 1 и камню 2 равны

;

V_B1 = V_B2 = ω₁ l_{O В} .

Скорость точки В₃ кулисы 3

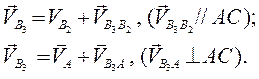
Скорость точки С₃ кулисы определяем по правилу подобия

,

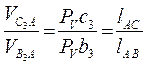откуда   Р _V c ₃ = Р _V b₃∙ l_CA / l_{A В}  .

Скорости точек С₄ и С₃, принадлежащих соответственно звеньям 4 и 5

.

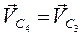Скорость D звена 5

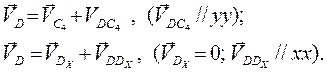
На рис. 4.5. слева внизу изображен план скоростей.

Пользуясь планом скоростей, определяем скорости точек  D и C :

V_D = (Р _V d)μ_V;   V _С = (Р _V с)μ_V.

Угловая скорость кулисы, направленная по вращению часовой стрелки, равна

ω₃ = ω₂ = (Р _V с)μ_V / l_CB .

Относительная скорость 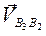 кулисы 3 относительно камня 2 направлена вниз параллельно звену ВС и равна

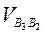= (b₂ b₃)μ_V.

(Индексами в скобках обозначены длины отрезков на плане скоростей в миллиметрах).

Перейдем к определению ускорений точек и звеньев механизма.

Ускорения точек B₁ и В₂ , принадлежащих соответственно кривошипу 1 и камню 2:

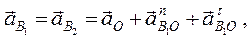
где ,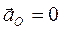

нормальное (центростремительное) ускорение 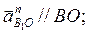 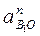 = ω₁² l_OB;

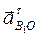
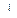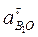тангенциальное (касательное) ускорение B О; = ε₁ l_OB = 0,

так как в рассматриваемом примере угловое ускорение кривошипа ε₁ = 0.

Построение плана ускорений показано на рис. 4.5.

Запишем векторные уравнения для определения ускорения точки В₃  кулисы АС:

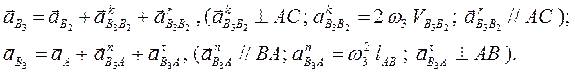
Ускорение точки С кулисы определяем по правилу подобия

,

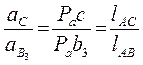откуда   Р_а c = (Р_а a₃) ∙ l _АС / l _АВ .

Ускорение точки D звена 5 найдем из графического решения следующих векторных уравнений:

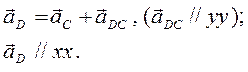
Пользуясь планом ускорений, определяем ускорения  точек

a_D = (Р _a d)μ_a ; a _С = (Р _a с)μ_a ; a_A3 = (Р _a а₃)μ_a .

Угловое ускорение кулисы направлено по вращению часовой стрелки и равно

ε ₃ = ε ₂ = (nb₃)μ_a / l_AB .

Метод графического дифференцирования и интегрирования

Если известна графическая зависимость «S_B – t » перемещения S_B  точки В от времени t , то для определения зависимости скорости этой точки от времени можно воспользоваться методом графического дифференцирования.

Рассмотрим построение диаграммы скорость – время « V_B – t», если задан график перемещение – время  «S_B – t » и масштабные коэффициенты времени μ_t и перемещения μ_S .

Если перемещение S на диаграмме задано дискретно, то при построении кинематических диаграмм используют метод хорд, заменяя заданную кривую графиком в виде ломаной линии.

Дана диаграмма перемещение-время” для движущейся точки (рис..4.6, вверху).

Под диаграммой S = S(t)строим прямоугольную систему координат. Ось времени разбиваем на такие же отрезки, что и на графике перемещения.

Рис. 4.6. Графическое дифференцирование методом хорд

От начала координат влево откладываем отрезок H и обозначаем полюс p.

Из полюса р проводим прямые pb ' // ab; pc ' // bc; pd ' // cd и т.д. Сносим полученные точки b ', c ', d ' и т.д. на соответствующие отрезки времени и получаем ступенчатый график скорости. В середине каждого отрезка помечаем точки b₁, c₁, d₁ и т.д. и соединяем их плавной кривой.

Масштабный коэффициент скорости μ_V = μ_S /(H μ_t ), м/(с мм).

Графическое интегрирование осуществляется как действие, обратное графическому дифференцированию. Рассмотрим применение метода графического интегрирования на конкретном примере.

Дано: графическая зависимость «М – φ» момента силы от угла поворота звена приложения этого момента (рис. 4.7). Угол φ задан в радианах. Даны также масштабные коэффициенты μ_М (Н м/мм) и μ_φ (рад/мм).

Требуется: построить график «А–φ» работы этого момента

.

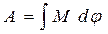Ось абсцисс разбивается на некоторое число шагов 1, 2, 3,... В пределах каждого шага интегрируемую функцию считают постоянной. Осреднение производят по равенству площадей трапеции и заштрихованного прямоугольника для каждого шага. Среднее значение ординаты на каждом шаге проецируют на ось ординат и полученные точки 1′′, 2′′, 3′′,… соединяют прямыми с полюсом Р, расположенным на оси абсцисс слева от начала координат на полюсном расстоянии Н.

Рис. 4.7. Графическое интегрирование

Для построения искомой интегральной кривой строят ломаную кривую, ординаты которой получают следующим образом: на первом шаге 0–1 проводят из начала координат отрезок 01′′′, параллельно прямой P1′′. Из правого конца этого отрезка на втором шаге 1–2 проводят отрезок 1′′′2′′′, параллельно прямой P2′′, и т.д. Масштабный коэффициент построенного графика равен μ_А=Н μ_φ μ_М.

 

5. ДВИЖЕНИЕ МАШИНЫ ПОД  ДЕЙСТВИЕМ ЗАДАННЫХ СИЛ

В настоящей главе  рассмотрена задача определения момента инерции маховых масс машины по заданному коэффициенту неравномерности хода машины.

Будем рассматривать механизмы с жесткими звеньями и с одной степенью подвижности, а силы, действующие на механизм, считаем известными в каждом положении механизма.

Основные понятия и термины

Уравнение движения

Для механизмов с одной степенью подвижности наиболее простое решение получается при использовании уравнения движения машины в виде

ΔТ = Т – Т₀ = ΣА,

т.е. приращение кинетической энергии ΔТ механизма при переходе из начального положения в рассматриваемое равно сумме работ всех внешних сил, действующих на звенья механизма. При этом 

Σ А = А_ДВ + А_С + А _G ,                                    (5.1)

где А_ДВ , А_С и А _G – работа соответственно сил движущих (А_ДВ > 0), сил сопротивления (А_С < 0) и сил тяжести.

Динамическая модель механизма

В общем случае пользоваться уравнением (5.1) сложно, так как механизм может иметь много звеньев с различными массами и скоростями: на звенья действуют различные силы. Для механизмов с одной степенью подвижности удобно использовать одномассовую динамическую модель механизма (рис. 5.1).

 При исследовании этой мо­дели принимают следующие допущения: все звенья считаются абсолютно твердыми, кинематические па­ры недеформируемыми. Зазоры в парах отсутствуют.

На рис. 5.1, а  изображена кинематическая схема кривошипно-ползунного рычажного механизма с жесткими звеньями и одной степенью свободы. Движение всех звеньев такого меха­низма полностью определяется законом движения (φ, ω, ε) начального звена ОА, где φ – угол поворота; ω – угловая скорость, а ε – угловое ускорение начального звена.

Для отыскания этого закона движения с учетом сил F_C и M_C , действующих на механизм, используют одну из двух представленных на рис. 5.1 динами­ческих моделей.

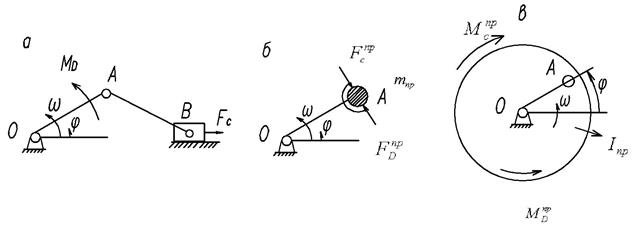
Рис. 5.1. Динамические модели механизма с жесткими звеньями:

а − кинематическая схема механизма; б и в – динамические модели механизма

На рис. 5.1, в представлена динамическая модель, в которой масса всех звеньев заменяется приведенным моментом инерции I _пр  диска, жестко связанного со звеном ОА. Силы, действующие на механизм в этом случае, заменяются приведенными моментами сил М_С^пр и М _D ^пр . При использовании обеих динамических моделей (рис. 5.1,б и 5.1,в) результаты расчета закона движения звена ОА будут одинаковы.

Приведенной массой m_пр называется такая условная масса, сосредоточенная в точке приведения, кинетическая энергия которой равна сумме кинетических энергий приводимых звеньев в данном положении механизма:

  .

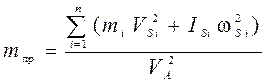При приведении масс к вращающемуся звену (рис. 5.1,в) удобнее пользоваться понятием приведенного момента инерции I_np относительно оси вращения звена приведения:

 ,

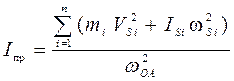где m_i , I_{S i} – масса и осевой момент инерции относительно оси, проходящей через центр масс i -го звена; V_{S i} , ω_i – соответственно скорость масс i -го звена и угловая скорость

i -го звена; V_A – скорость точки приведения; ω_ОА – угловая скорость звена приведения.

Приведенной силой (моментом) называют условную силу (момент), которая, будучи приложена к звену приведения, развивает мощность Р, равную мощности приводимых сил и моментов в рассматриваемом положении механизма.

Величина приведенной силы, направленной по скорости точки приведения, равна

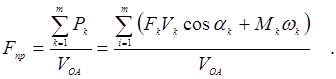
Приведенный момент силы равен

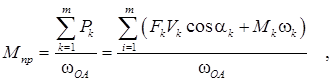
где F_k – величина приводимой силы, приложенной в точке k механизма;

V_к – скорость точки k;  α_k –угол между векторам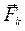и  и 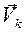. M_k – момент, приложенный к звену k ; ω_k – угловая скорость k- го звена.

Из формул следует, что приведенная масса и приведенная сила зависят от отношения квадратов скоростей приводимых звеньев к квадрату скорости звена

приведения. Таким образом, приведенная сила и приведенная масса являются функцией обобщенной координаты.

Режимы движения машины

На рис. 5.2 показана графическая зависимость скорости ω на­чального звена механизма с одной степенью свободы от времени t.Полное время движения машины можно разделить на три участка, соответствующих следующим режимам движения.

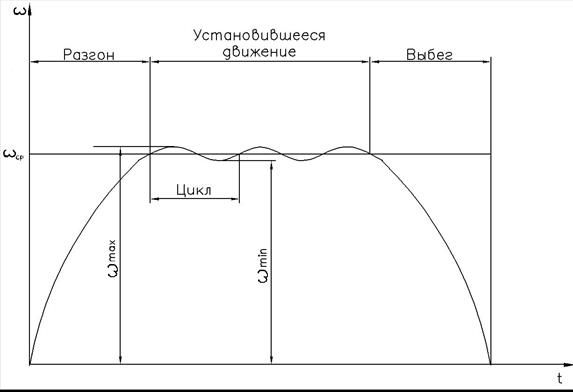
Рис. 5.2. Тахограмма движения начального звена механизма

Разгон, в процессе которого происходит постепенное возрас­тание скорости начального звена от нуля до среднего значения ω_ср. Энергети­ческую характеристику этого периода: А _D > A_C.

При установившемся движении скорость начального звена периодически изменяется около одного и того же среднего значения ω_ср. Минимальный промежуток времени, по истечении которого начальное звено возвращается в первоначальное положение, имея первоначальное значение скорости, называется циклом установившегося движения. Энергетическая характеристика этого режима движения за цикл установившегося движения: А _D = A_C .

Выбег характеризуется постепенным уменьшением скорости начального звена от среднего значения ω_ср до нуля. Энерге­тическая характеристика выбега: А _D < A_C .

Для машин, в которых преобладает установившийся ре­жим движения, одним из критериев работоспособности является коэффициент δ неравномерности установившегося движения

δ = (ω_max − ω_min)/ ω_ср,

где ω_max,  ω_min, ω_ср – соответственномаксимальное, минимальное и среднее значения угловой скорости начального звена за цикл.

---

Дата добавления: 2018-10-27; просмотров: 989; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!