Иначе говоря, математическое ожидание какого-либо события равно абсолютной велнчине этого события, умноженной на вероятность его наступления.
Например, имеются два варианта вложения капитала. Установлено, что при вложении капитала в мероприятие А получение прибыли в сумме 250 тыс. руб. имеет вероятность 0,6, а в мероприятие Б – получение прибыли в сумме 300 тыс. руб. имеет вероятность 0,4. Тогда ожидаемое получение прибыли от вложения капитала (т. е. Математическое ожидание) составит
– по мероприятию А – 150 тыс. руб. (250 х 0,6);
– по мероприятию Б – 120 тыс. руб. (300 х 0,4).
Вероятность наступления события может быть определена объективным или субъективным методом.
Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие. Например, если известно, что при вложении капитала в какое-либо мероприятие прибыль в сумме 250 тыс. руб. была получена в 120 случаях из 200, то вероятность получения такой прибыли составляет 0,6 (120:200).
Субъективный метод определения вероятности основан на использовании субъективных критериев, которые базируются на различных предположениях. К таким предположениям могут относиться: суждение и личный опыт оценивающего, оценка эксперта, мнение финансового консультанта и т. п. Когда вероятность определяется субъективно, то разные люди могут устанавливать разное ее значение для одного и того же события и делать каждый свой выбор.
Важное место при этом занимает экспертная оценка, т. е. Проведение экспертизы, обработка и использование ее результатов при обосновании значения вероятности.
|
|
|
Принятие экспертной оценки представляет собой комплекс логических и математико-статистических методов и процедур, связанных с деятельностью эксперта по переработке необходимой для анализа и принятия решений информации. Экспертная оценка основана на использовании способности специалиста (его знаний, умения, опыта, интуиции и т. п.) находить нужное, наиболее эффективное решение.
Величина риска (степень риска) измеряется двумя критериями:
58.среднее ожидаемое значение;
59.колеблемость (изменчивость) возможного результата. Среднее ожидаемое значение – это то значение величины события, которое связано с неопределенной ситуацией. Среднее ожидаемое значение является средневзвешенным для всех возможных результатов, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения.
Среднее ожидаемое значение измеряет результат, который мы ожидаем в среднем.
Тоесть, если известно, что при вложении капитала в мероприятие А из 120 случаев прибыль 250 тыс. руб. была получена в 48 случаях (вероятность 0,4), прибыль 200 тыс. руб. была получена в 36 случаях (вероятность 0,3) и прибыль 300 тыс. руб. была получена в 36 случаях (вероятность 0,3), то среднее ожидаемое значение составит (250 х 0,4 + 200 х 0,3 + 300 х 0,3) = 250 тыс. руб.
|
|
|
Аналогично было найдено, что при вложении капитала в мероприятие Б средняя прибыль составила (400 х 0,3 + 300 х 0,5 + 150 х 0,2) = 300 тыс. руб.
Сравнивая две суммы ожидаемой прибыли при вложении капитала в мероприятия А и Б, можно сделать вывод, что при вложении в мероприятие А величина получаемой прибыли колеблется от 200 до 300 тыс. руб. и средняя величина составляет 250 тыс. руб.; при вложении капитала в мероприятие Б величина получаемой прибыли колеблется от 150 до 400 тыс. руб. и средняя величина составляет 300 тыс. руб.
Средняя величина представляет собой обобщенную количественную характеристику и не позволяет принять решения в пользу какого-либо варианта вложения капитала.
Для окончательного принятия решения необходимо измерить колеблемость показателей, т. е. Определить меру колеблемости возможного результата.
Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины.
Для этого на практике обычно применяются два близко связанных критерия: дисперсия и среднее квадратическое отклонение.
Дисперсия представляет собой средневзвешенное из квадратов отклонений действительных результатов от средних ожидаемых.
|
|
|

где σ2 – дисперсия;
х – ожидаемое значение для каждого случая наблюдения;
 – среднее ожидаемое значение;
– среднее ожидаемое значение;
 п – число случаев наблюдения (частота).
п – число случаев наблюдения (частота).
Среднее квадратическое отклонение определяется по формуле:

При равенстве частот имеем частный случай:


Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.
Для анализа обычно используют коэффициент вариации. Он представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений.
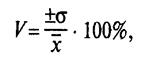
где V – коэффициент вариации, %;
60.– среднее квадратическое отклонение;
 – среднее ожидаемое значение.
– среднее ожидаемое значение.

Коэффициент вариации – относительная величина. Поэтому на размер этого коэффициента не оказывают влияние абсолютные значения изучаемого показателя. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации может изменяться от 0 до 100 %. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации:
|
|
|
до 10 % – слабая колеблемость;
10—25 % – умеренная колеблемость;
свыше 25 % – высокая колеблемость.
Расчет дисперсии при вложении капитала в мероприятия А и Б приведен в табл. 12.2.
Таблица 12.2
Дата добавления: 2018-10-26; просмотров: 579; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
