Величина наращенной суммы в зависимости от вида процентной ставки

Р = 10 000 ам. Дол., величина процентной ставки – 10 %

Величина наращенной суммы	n = 1	n = 3	n = 6
S = P(1+ in)	11 000	13 000	16 000
S = P(1+ I) n	11 000	13 310	17 716
S = Peⁱⁿ	11 052	13 499	18 222
S = P/(1 – dn)	11 111	14 286	25 000
S = P/(1 – d)n	11 111	13 717	18 816

Результаты вычислений, вероятно, будут неожиданными для большинства читателей. Наибольший рост капитала мы имели бы в случае начисления процентной по простой учетной ставке. (Следует заметить, что на практике она не применяется на длительных, больше года, периодах начисления).

Однако для того, чтобы выбрать в каждом конкретном случае наиболее выгодную процентную ставку, не обязательно считать получаемые суммы.

Эквивалентность процентных ставок различного типа

Часто при расчетах, проводимых по различным финансовым операциям, возникает необходимость в определении эквивалентных процентных ставок.

Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дают одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требует инструмент для коррективного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок используют уравнение эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Вспомним обозначения, использованные ранее:

I – простая годовая ставка ссудного процента;

d – простая годовая учетная ставка;

i_c – сложная годовая ставка ссудного процента;

d_c – сложная годовая учетная ставка;

j – номинальная ставка ссудного процента;

f – номинальная учетная ставка.

Повторим формулы для определения наращенной суммы при различных способах начисления процентов, полученные в предыдущих параграфах этой главы:

S = P(1+ ni);

S = P/(1– nd);

S = P(1+ I_c)ⁿ;

S_mn = P(1+ j / m)^mn;

S = P/(1 – d_c)ⁿ;

S = P/(1 – f / m)^mn.

Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.

Рассмотрим несколько случаев.

Приравнивая соотношения S = P(1+ ni) и S = P/ (1 – nd), получим:

откуда:

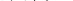Из формул S = P(1+ ni) и S = P (1+ I_c)ⁿ имеем:

1+ ni = (1+ I_c)ⁿ;

I = [(1+ I_c)ⁿ – 1] / n;

I_c = ⁿ√1+ ni – 1.

Приравнивание формул S = P(1+ ni) и S_mn = P (1+ j / m)^mn дает

I + ni = (1+ j / m)^mn;

Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы S = P (1+ I_c)n и S_mn = P (1+ j / m)^mn:

(1+ I_c)n = (1+ j / m)^mn;

I_c = (1+ j / m)^m – 1;

Полученная по формуле i_c = (1+ j / m)^m – 1 годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной процентной ставки больше значения номинальной, а совпадают они при m = 1.

Далее из формул S = P (1+ I_c)n и S = P / (1 – dc)ⁿ имеем:

Аналогичным образом получаем зависимости между любыми другими эквивалентными процентными ставками.

Проанализировав полученные формулы, можно сделать два замечания.

1. Эквивалентность различных процентных ставок никогда не зависит от величины первоначальной суммы р (для данного рассматриваемого случая, когда первоначальная сумма р предполагается одинаковой).

2. Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления за исключением случая эквивалентности между собой сложных процентных ставок разного вида (если период начисления один и тот же).

Используя для вычислительной формулы S = P (1+ i_c)ⁿ и S = P / (1 – dc)_n, можно построить таблицу, отражающую зависимость между эквивалентными сложными учетными ставками и ставками ссудных процентов (табл. 2). Видно, что небольшие учетные ставки имеют эквивалентные ставки ссудного процента, сопоставимые по величине, но с ростом учетных ставок разница увеличивается очень быстро.

Таблица 1.2

Дата добавления: 2018-10-26; просмотров: 314; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!