Простые и сложные проценты. Учет по простым и сложным учетным ставкам
Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет срок менее 1 года), или когда после каждого интервала начисления кредитору выплачиваются проценты. Естественно, простые ставки ссудных процентов могут применяться и в любых других случаях по договоренности участвующих в операции сторон.
Введем следующие обозначения:
I (%) – простая годовая ставка ссудного процента;
I – относительная величина годовой ставки процентов;
Ig – сумма процентных денег, выплачиваемых за год;
I – общая сумма процентных денег за весь период начисления;
P – величина первоначальной денежной суммы;
S – наращенная сумма;
k – коэффициент наращения;
n – продолжительность периода начисления в годах;
d – продолжительность периода начисления в днях;
K – продолжительность года в днях.
Величина К является временной базой для расчета процентов.
В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный (коммерческий) процент.
Дата выдачи и дата погашения ссуды всегда считаются за один день, при этом возможны два варианта:
1. Используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответствующего дню окончания займа, вычитают номер первого дня.
2. Берется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30-ти дням; этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.
Точный процент получают, когда за временную базу берут фактическое число дней в году (365 и 366) и точное число дней ссуды.
 |  |  |  | ||||||
 | |||||||||
Приведенным выше определениям соответствуют следующие формулы:
Применяя последовательно выше рассмотренные формулы, получим основную формулу для определения наращенной суммы долга:
S = P (I + ni).
На практике часто возникает обратная задача: узнать величину суммы P, которая в будущем должна составить заданную величину S. В этом случае P называется современной (текущей, настоящей, приведенной) величиной суммы S.
Определение современной величины P наращенной суммы S называется дисконтированием, а определение величины наращенной суммы S – компаундингом.
В применении к ставке ссудного процента может также встретиться название математическое дисконтирование, несовместимое, кстати говоря, с учетными ставками, которые будут рассматриваться в следующем разделе.
Из формулы S = P (I + ni) получаем формулу, соответствующую операции дисконтирования:
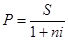
 |  |  | |||||
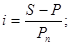 | |||||||
Преобразуя формулу S = P (I + ni) (т. е. Заменяя входящие в нее выражения на эквивалентные и выражая одни величины через другие), получаем еще несколько формул для определения неизвестных величин в различных случаях:
Иногда на различных интервалах начисления применяются разные процентные ставки. Если на последовательных интервалах начисления n1, n2, …, nN используются ставки процентов i1, i2, …, i n , то по формулам в конце первого интервала составит:
 |
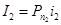 |
в конце второго интервала:
и т. д.
При N интервалах начисления наращенная сумма составит:
 .
.
Для множителя наращения, следовательно, имеем:
 .
.
При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (т. е. Из наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке, а также коммерческим или банковским учетом.
Дисконт – это доход, полученный по учетной ставке, т. е. Разница между размером кредита и непосредственно выдаваемой суммой.
Пусть теперь
d (%) – простая годовая учетная ставка;
d – относительная величина учетной ставки;
Dг – сумма процентных денег, выплачиваемая за год;
D – общая сумма процентных денег;
S – сумма, которая должна быть возвращена;
P – сумма, получаемая заемщиком.
 |
Тогда, согласно определениям, имеем следующие формулы:
D г = d S;
D = n D г = n d S;
P = S – D = S(1 – nd) = S[1 – (д/K)d].
Преобразуя последнее выражение, получаем формулу для определения наращенной суммы:
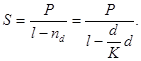 |
Из этой формулы легко видеть, что в отличие от случая простых ставок ссудного процента, простые учетные ставки не могут принимать любые значения. Именно для того, чтобы выражение имело смысл, необходимо, чтобы знаменатель дроби в правой части был строго больше нуля, т. е. (1 – nd) > 0, или d < 1/n. Правда, со значениями d, близкими к предельным, вряд ли можно встретиться в жизни.
На практике учетные ставки применяются, главным образом, при учете (т. е. Покупке) векселей и других денежных обязательств. Вопрос получения дохода по векселям будет подробно рассмотрен далее.
 |  |
Из приведенных формул можно вывести еще две формулы для определения периода начисления и учетной ставки при прочих заданных условиях:
Если после очередного интервала начисления доход (т. е. Начисленные за данный интервал проценты) не выплачивается, а присоединяется к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.
Пусть
Ic – относительная величина годовой ставки сложных ссудных процентов;
k н.c – коэффициент наращения в случаях сложных процентов;
j – номинальная ставка сложных ссудных процентов (ее определение будет дано в дальнейшем).
Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой S = P (I + ni) составит:
S1=P (1 + I с).
Еще через год это выражение применяется уже к сумме S1:
S2 = S1 (1 + I с) = P (1 + I с)²
и так далее. Очевидно, что по прошествии n лет наращенная сумма составит:
S = P (1 + I с)ⁿ.
Множитель наращения k н.с., соответственно, будет равен:
kн.с. = (1 + I с)ⁿ.
При начислении простых процентов он составил бы по формулам:

Сравнивая два последних выражения для коэффициентов наращения, можно видеть, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов.
Если все интервалы начисления одинаковы (как и бывает обычно на практике) и ставка сложных процентов одна и та же, формула принимает вид:
SN = P(1 + ni)N.
Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j – годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.
При m равных интервалах начисления и номинальной процентной ставки j эта величина считается равной j/m.
Если срок ссуды составляет n лет, то, аналогично формуле S = P (1 + iс)ⁿ, получаем выражение для определения наращенной суммы:
S mn = P(1 + j / m)mn,
где mn – общее число интервалов начисления за весь срок ссуды.
Если общее число интервалов начисления не является целым числом (mn − целое число интервалов начисления, l – часть интервала начисления), то выражение принимает вид:
S = P(1 + j / m)mn (1 + lj / m).
Для целого числа периодов начисления используется формула сложных процентов S = P (1 + iс)ⁿ, а для оставшейся части – формула простых процентов S = P (1 + ni).
В Республике Беларусь в настоящее время наиболее распространенным является начисление процентов по полугодиям, поквартальное и ежемесячное (иногда интервалом начисления может являться и день). Такие проценты, начисляемые с определенной периодичностью, называются дискретными.
В мировой практике часто применяется также непрерывное начисление сложных процентов (т. е. Продолжительность интервала начисления стремится к нулю, а m – к бесконечности).
 |
В этом случае для вычисления наращенной суммы служит следующее выражение:
Для расчетов можно использовать известную в математике формулу:
 |
где е = 2,71828…
 |
Из этой формулы следует:
 |
Тогда для наращенной суммы получаем
 |
Здесь
Значения наращенной суммы S можно вычислять с помощью финансового калькулятора или находя значение e jn и других требуемых величин в специальных таблицах.
Очевидно, что непрерывный способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях (т. е. При одинаковых n, j, P).
Аналогично случаю простых процентов полученные формулы можно преобразовывать, выражая одни величины через другие, в зависимости от того, что известно, а что требуется найти.
 |
Так, из формулы S = P (1 + iс)ⁿ получаем
Напомним, что, как и в случае простых процентов, определение современной величины суммы S называется дисконтированием.
Коэффициент дисконтирования a является величиной, обратной коэффициенту наращения, т. е. Кн.с.* а = 1.
 |
Формула
а также соответствующие формулы для случая простых ставок ссудного процента и для учетных ставок дают легко понять, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок получения и чем выше норма доходности.
 |
Также из формулы S = P (1 + iс)ⁿ имеем:

Из формулы S mn = P(1 + j / m)mn:
Применяя операцию логарифмирования к обеим частям формулы S = P (1 + iс)ⁿ, получаем:

Подобным же образом из формулы S mn = P(1+j / m)mn получаем формулу:
 |
Если нет специального калькулятора, значения логарифмов также находят по таблицам.
Рассмотрим теперь антисипативный способ начисления сложных процентов.
Пусть
dс (%) – сложная годовая учетная ставка;
dc – относительная величина сложной учетной ставки;
k н.у. – коэффициент наращения для случая учетной ставки;
f – номинальная годовая учетная ставка.
Тогда по прошествии первого года наращенная сумма S 1 в соответствии с формулой составит: 
Еще через год эта формула будет применяться уже к сумме S1:
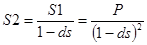
и т. д., аналогично случаю сложных ставок ссудных процентов.
 |
По прошествии n лет наращенная сумма составит
Отсюда для множителя наращения имеем
 |
 |  |
Сравнивая формулы S = P(1+ ic)ⁿ и
легко видеть, что при равенстве ссудного процента и учетной ставки наращение первоначальной суммы во втором случае (антисипативный метод) идет быстрее.
Поэтому в литературе часто можно встретить утверждение, что декурсивный метод начисления более выгоден для заемщика, а антисипативный – для кредитора. Это можно считать справедливым для небольших процентных ставок, когда расхождение не столь значительно. Но с ростом процентной ставки разница в величине наращенной суммы становится огромной (при этом она сама растет с ростом n), и сравнение двух методов, с точки зрения выгодности, утрачивает смысл.
Для начисления процентов m раз в году формула имеет такой вид:
S = P/(1 – f/m)mn или
S = P/[(1– f/m)mn(1-lf/m)].
При этом mn – целое число интервалов начисления за весь период начисления, l – часть интервала начисления.
При непрерывном начислении процентов S рассчитывается по формуле:
S = P/lim (1–f/m)mn.
M→∞
Из полученных формул путем преобразования получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки:
 |
Мы рассмотрели различные способы начисления процентов. В заключение составим таблицу, дающую возможность наглядного представления результатов, получаемых при этих способах для одной и той же первоначальной суммы, одинаковых по величине процентных ставок и периодов начисления n.
Таблица 1.1
Дата добавления: 2018-10-26; просмотров: 647; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
