Уравнение прямой с угловым коэффициентом.
Уравнение прямой вида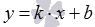 
, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). Уравнения прямой с угловым коэффициентом нам хорошо известны из курса алгебры средней школы. Такой вид уравнения прямой очень удобен для исследования, так как переменная y представляет собой явную функцию аргумента x.
Определение углового коэффициента прямой дается через определение угла наклона прямой к положительному направлению оси Ox.
Определение.
Углом наклона прямой к положительному направлению оси абсцисс в данной прямоугольной декартовой системе координат Oxy называют угол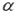 
, отсчитываемый от положительного направления оси Ох до данной прямой против хода часовой стрелки.
Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю.
Определение.
Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть,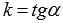 
.
Если прямая параллельна оси ординат, то угловой коэффициент обращается в бесконечность (в этом случае также говорят, что угловой коэффициент не существует). Другими словами, мы не можем написать уравнение прямой с угловым коэффициентом для прямой, параллельной оси Oy или совпадающей с ней.
Заметим, что прямая, определяемая уравнением 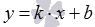, проходит через точку 
на оси ординат.
Таким образом, уравнение прямой с угловым коэффициентом 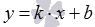определяет на плоскости прямую, проходящую через точку и образующую угол 
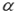с положительным направлением оси абсцисс, причем .
|
|
|
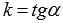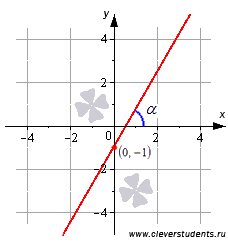
В качестве примера изобразим прямую, определяемую уравнением вида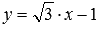 
. Эта прямая проходит через точку 
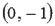и имеет наклон 
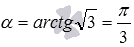радиан (60градусов) к положительному направлению оси Ox. Ее угловой коэффициент равен 
.
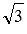Отметим, что уравнение касательной к графику функции в точке очень удобно искать именно в виде уравнения прямой с угловым коэффициентом.
Каноническое уравнение прямой на плоскости.
Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид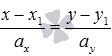 
, где 
и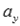 
– некоторые действительные числа, причем 
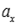и 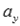одновременно не равны нулю.
Очевидно, что прямая линия, определяемая каноническим уравнением прямой, проходит через точку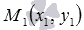 
. В свою очередь числа 
и 
, стоящие в знаменателях дробей, представляют собой координаты направляющего вектора этой прямой. Таким образом, каноническое уравнение прямой 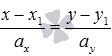в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку 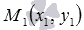и имеющей направляющий вектор 
.
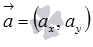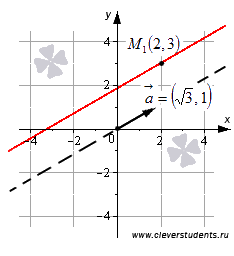
Для примера изобразим на плоскости прямую линию, соответствующую каноническому уравнению прямой вида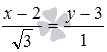 
. Очевидно, что точка 
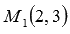принадлежит прямой, а вектор 
является направляющим вектором этой прямой.
|
|
|
Каноническое уравнение прямой вида 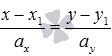используют даже тогда, когда одно из чисел 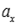или 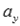равно нулю. В этом случае запись 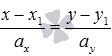считают условной (так как содержится ноль в знаменателе) и ее следует понимать как 
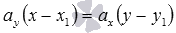. Если 
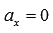, то каноническое уравнение принимает вид 
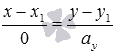и определяет прямую, параллельную оси ординат (или совпадающую с ней). Если 
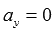, то каноническое уравнение прямой принимает вид 
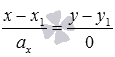и определяет прямую, параллельную оси абсцисс (или совпадающую с ней).
Дата добавления: 2018-10-26; просмотров: 901; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!