Примеры элементарных преобразований
Продемонстрируем все элементарные преобразования на примере матрицы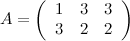 
Умножим первую строку матрицы на два, то есть каждый элемент первой строки умножаем на двойку, в результате получим матрицу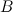 
, эквивалентную заданной матрице 
:
Поменяем первую и вторую строки матрицы 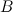местами, получаем эквивалентную ей матрицу 
:
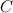От первой строки матрицы 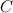отнимем вторую строку, получаем эквивалентную матрицу 
:
В итоге делаем вывод, что матрицы и эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.
Теорема Кронекера-Капелли. СЛАУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Пример
Задание. При каких значениях 
система 
будет совместной?
Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы 
(слева от вертикальной черты находится матрица системы ):
и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от первой строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:
Третью строку складываем с первой:
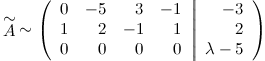
и меняем первую и вторую строки матрицы местами
Матрица приведена к ступенчатому виду. Получаем, что 
, 
. Таким образом, при 
система совместна, а при 
- несовместна.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
|
|
|
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 
+ x2 
+ … + xn 
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений:
A = 
~ 
. 
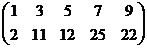RgA = 2.
A* = 
RgA* = 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
А = 
; 
= 2 + 12 = 14 не равно 0; RgA = 2;
A* = 
RgA* = 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
Билет 7. Второй метод вычисления обратной матрицы. Упрощённый метод вычисления определителя.
Метод элементарных преобразований
Для применения этого метода в одну матрицу записывают заданную матрицу A и единичную матрицу E, т.е. составляют матрицу вида (A|E) (эту матрицу называют также расширенной). После этого с помощью элементарных преобразований, выполняемых со строками расширенной матрицы, добиваются того, что матрица слева от черты станет единичной, причём расширенная матрица примет вид (E|A−1). К элементарным преобразованиям в данной ситуации относят такие действия:
|
|
|
1.Смена мест двух строк.
2.Умножение всех элементов строки на некоторое число, не равное нулю.
3.Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Вычисление обратной матрицы
Если с помощью элементарных преобразований строк квадратную матрицу A можно привести к единичной матрице E, то при таких же элементарных преобразованиях над матрицей E получим 
Пример.
Вычисление определителей
При вычислении определителей разрешается применять все 6 видов преобразований. Следует иметь в виду, что:
1) при преобразованиях 1 и 4 определитель меняет знак;
2) при преобразованиях 2 и 5 значение определителя умножается на то число, на которое умножается строка или столбец;
3) при преобразованиях 3 и 6 определитель не изменяется.
Общая схема вычисления определителя такова:
1) Если все элементы первого столбца равны нулю, то определитель равен нулю и вычисление определителя заканчивается.
|
|
|
2) Если в первом столбце есть ненулевой элемент, то перестановкой строк его можно перенести в первую строку. При этом перед определителем меняется знак.
3) Если a11 не равен 0, то умножаем первую строку на (a11 )-1. При этом перед определителем пишем множитель a11.
4) Для каждого i 
1 прибавляем к i-той строке 1 -ю строку, умноженную на (–a i 1 ). Полученная матрица имеет 1-упрощенный вид.
5) Разлагаем определитель по первой строке и сводим задачу к вычислению определителя матрицы меньшего порядка.
6) Повторяя шаги 1-5) несколько раз, мы сводим задачу к вычислению определителей 2 или 3 порядка, которые можно вычислить по известным формулам.
Пример. Вычислить определитель:
Решение:
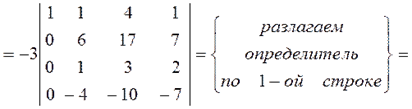
Билет 8. Различные виды уравнений прямой на плоскости.
Дата добавления: 2018-10-26; просмотров: 389; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!