Методы изучения движения жидкости
Существует 2 метода: Лагранжа и Эйлера
1) Метод Лагранжа: Жидкость разделяют на жидкие частицы и составляют уравнения траектории. При этом каждую жидкую частицу принимают за отдельное твердое тело. Для точного описания течения жидкости, жидкие частицы должны быть достаточно малы. Обычно метод не часто используется из-за огромных вычислений и т.п.
2) Метод Эйлера: В методе Эйлера составляют систему уравнений, описывающее поле скорости:
Общие положения(дополнительно):
Жидкая частица – в гидромеханике изучаем сплошную жидкость, которую можно делить на части – жидкие частицы. Если устремить количество сечений к бесконечности, то жидкая частица бесконечно мала => элементарная жидкая частица.
Поле скорости – если в каждой точке заданной области жидкости соответствует вполне определенное значение скорости, говорят, что задано поле скорости. 
Скорость заданной точки – скорость жидкой частицы, проходящая в данный момент через данную точку.
Линия тока и ее уравнение. Трубка тока и жидкая струйка.
Линия тока – линия, в каждой точке которой направление касательной к этой линии и скорость в этой точке совпадает.
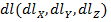
Свойство непротекаемости: На любой твердой поверхности S нормальная к ней проекция скорости = 0(V п =0).
Поверхность тока – совокупность линий тока, проходящих через заданную линию над поверхностью тела. Поверхность тока, образованная замкнутым контуром, называется трубкой тока.
|
|
|
Свойство: Расход жидкости через трубку тока = 0, так как на ней V п =0
Поток, текущий внутри трубки тока, называется жидкой струей. Течение жидкой струи перпендикулярное линиям тока, называется живым сечением трубы.
Течение, в котором живые сечения могут быть аппроксимированы плоскостями, называется плавно-изменяющимся сечениями.
В живом течении с плавно-изменяющимся сечениями, давление подчиняется основному закону гидростатики. 
Линию тока можно рассматривать как жидкую струю с площадью сечения → 0.
Нулевая линия тока – линия тока, проходящая по поверхности тела.(А,В - критические точки).
Свойства линий тока жидких струй:
· Линии тока не пересекаются, т.к. их пересечение означает, что в точке пересечения скорость жидкости имеет 2 направления, что лишено физического смысла.
· Скорость точки, в которой пересекаются линии тока, называются критическими.
· Вектор скорости в критических точках вырождается в точку.
· Линии тока и струи не заканчиваются внутри жидкости и не могут притыкаться к ограниченным их твердым поверхностям.
Уравнение неразрывности в общем виде
Предварительно введем понятие расхода жидкости через поверхность, понимая под ним количество жидкости, протекающее через нее в единицу времени.
|
|
|
Объемным расходом жидкости Q через рассматриваемую поверхность S называется объем жидкости вытекающий через эту поверхность в единицу времени.
Массовым расходом жидкости М через рассматриваемую поверхность S называется массой жидкости вытекающей через эту поверхность за единицу времени.
В дальнейшем будем оперировать понятием объемного расхода. Для получения выражения расхода рассмотрим течение жидкости через неподвижную поверхность S. Выделим в ней элементарную площадку dS. Вектор скорости в центре площадки разложим на нормальную Un и касательную Ut составляющие. За время dt через поверхность dS протекает объем жидкости dQt = ( Undt ) dS , поскольку Ut вклада в расход жидкости через площадку не дает, элементарный расход dQ будет dQ / dt :
dQ = 
n dS 
Рассмотрим теперь течение жидкости через произвольную, неподвижную в пространстве, замкнутую поверхность S, охватывающую объем V. Закон сохранения массы сводится к тому, что массовый расход несжимаемой жидкости ( 
= const) через эту поверхность должен быть равен нулю, т.е. количество вытекающий из V жидкости должно быть равно количеству жидкости втекающией в этот V.
|
|
|
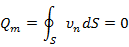
Это выражение представляет собой уравнение неразрывности для однородной несжимаемой жидкости в интегральной форме.
Преобразуем поверхностный интеграл:
Поскольку элемент объема dV положителен, это равенство справедливо лишь в том случае, когда для всех точек внутри объема:
Данное выражение представляет уравнение неразрывности для однородной несжимаемой жидкости в дифференциальной форме.
Дата добавления: 2018-09-20; просмотров: 571; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!