Свойства давлений в отсутствии касательных напряжений
Касательные напряжения – отношение касательной силы к площади ее приложения.
; 
Напряжения, действующие на произвольно ориентированную площадку:
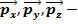напряжения, действующие на три взаимно перпендикулярные площадки, проходящую ч/з данную точку. Их можно представить в виде: (другие по аналогии) 
Подставляя (1) в (3), получим:
Подставим это в (2):
Учитывая, что:
|
Подставляем выражение для вектора нормали в (4) и, сравнивая коэффициенты при одинаковых ортах получаем: 
Это равенство позволяет сформулировать теорему о свойстве касательных напряжений:
Если в жидкости отсутствуют касательные напряжения, то нормальное напряжение в данной точке не зависит от ориентации площадки.
Зависимость имеет место в покоящейся вязкой и при движении и покое в невязкой жидкости.
Дифференциальное уравнение равновесия жидкости
Рассмотрим покоящуюся жидкость. Выберем некоторую точку О и возьмем ее за начало системы координат с осью oh направленной вертикально вниз, т.е. вдоль силы тяжести. Направление горизонтальных осей может быть произвольным.
Длины ребер примем бесконечно малыми и равными. dx, dy и dh. Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на g.
Сила гидростатического давления на любую грань равна произведению гидростатического давления на площадь этой грани.
Согласно принципу статики: Сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна 0.
|
|
– давление в начале координат):
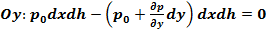
| Дифференциальное уравнение равновесия жидкости |
|
Основной закон гидростатики
Рассмотрев дифференциальное уравнение равновесия жидкости, можно заметить:
| Это значит, что в горизонтальной плоскости все точки имеют одинаковое давление! |
|
Следовательно, p ( x , y ) = C, в таком случае, выражение 
, можно записать не в частных, а в полных дифференциалах.
|
|
|
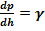или
Зная давление в одной точке жидкости, мы можем узнать давление во всех точках жидкости.
На практике начало координат выбирают в точке с известным давлением. Тогда в любой другой точке:
|
| Выражения в рамках называются законом гидростатики. |
Фактическое давление в данной точке называется абсолютным давлением.
Избыточное давление(p и) – разность между абсолютным давлением (р) и давлением в начале координат (р0).
Или, иначе, избыточное давление можно определить по следующей формуле:
В теории корабля начало координат выбирают на поверхности жидкости. Это давление называют атмосферным (рА)
В таком случае, основной закон гидростатики примет вид:
, где h – заглубление точки
Закон Паскаля
Определить силу от избыточных давлений, действующую на дно.
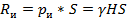Эта формула как раз и описывает закон Паскаля.
Словесно: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.
|
Рассмотрим 2 случая:
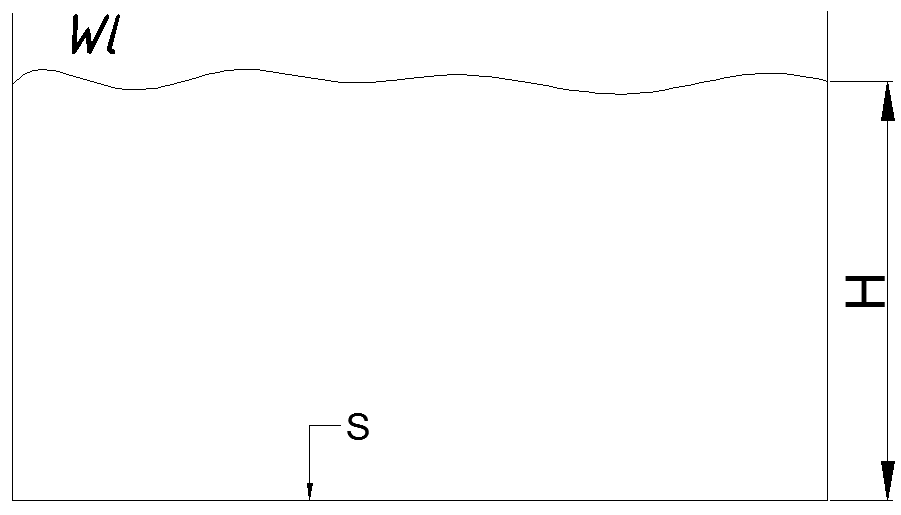
В обоих случаях силы от избыточных давлений, действующие на дно – одинаковы.(Так как и S и H одинаковы)
Согласно закону Паскаля работают такие устройства, как насосы или гидравлические прессы.
Закон Архимеда
Из лекций
Рассматривается тело, которое погружено в жидкость полностью или частично, не касается дна или стенок сосуда, а также других тел.
Результирующая гидроаэростатическая сила направлена вертикально вверх, проходит через центр подводного объема тела и численно равна:
RA - Архимедова сила
– удельный вес жидкости
V – объем подводной части тела
Из Ачкинадзе
Архимедовой силой поддержания или силой плавучести, действующая на погруженное в жидкость тело, равна весу жидкости в объеме тела и направлена вертикально вверх. Эта сила приложена в центре тяжести погруженного объема и направлена вертикально вверх.
Дата добавления: 2018-09-20; просмотров: 683; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!