Поле сферической, равномерно заряженной поверхности
Поверхностную плотность заряда на сфере S0 
будем считать постоянной. Очевидно, что эквипотенциальной поверхностью для сферической поверхности является сфера. Для любой точки поверхности сферы S(охватывающей заряженную сферу S0 и проходящей через точку с радиус-вектором r, в которой вычисляется поле), вектор напряжённости E параллелен вектору нормали к поверхности dS. Таким образом теорема Гаусса для сферической, равномерно заряженной поверхности принимает вид 
После несложных преобразований получаем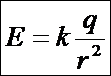 
для 
(вне сферы S0)
Для электростатического поля внутри заряженной сферы 
Поле внутри заряженной частицы равно нулю.
Теорема Гаусса в дифференциальной форме (вакуум).
Для того, чтобы записать теорему Гаусса в диф. форме, нужна математическая формула, описывающая связь интеграла по объёму с интегралом по поверхности, охватывающей этот объём – такую формулу называют теоремой Остроградского.
|
Поток вектора F через
замкнутую поверхность S
охватывающую объём V, равен
дивергенции этого вектора
из объёма V.
Применим теорему Остроградского к теореме Гаусса:
Дивергенция вектора напряжённости электростатического поля в любой точке пространства пропорциональна плотности заряда в этой точке.
Уравнение Пуассона (вакуум).
Электростатическое поле всегда потенциально. 
Следовательно, теорему Гаусса можно записать в виде
|
|
|
Эту формулу называют уравнением Пуассона для электростатического поля.
Таким образом, мы получили 2 способа описания электростатического поля:
| Основная задача электростатики | Дифференциальные уравнения |
| 
|
 
|  
|
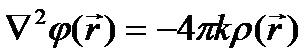
Уравнения, дающие решение основной задачи электростатики, являются решением дифференциальных уравнений электростатического поля – теоремы Гаусса и уравнения Пуассона.
13. Плотность заряда для точечного заряда (δ-функция).
Дельта - функция Дирака.
Качественно дельта-функцию можно определить следующим образом при условии, что
Важнейшим свойством δ–функции является следующее
Отметим некоторые полезные свойства δ-функции
Плотность заряда для точечного заряда (δ-функция).
Для того, чтобы записать теорему Гаусса в дифференциальной форме или уравнение Пуассона для точечного заряда необходимо выражение для плотности заряда точечного заряда. Формально, величину точечного заряда q можно записать через плотность заряда p, используя δ-функцию.
Следовательно, для точечного заряда 
Посмотрим использование этой формулы на примере основной задачи электростатики:
Таким образом, теорема Гаусса в дифференциальной форме для точечного заряда имеет вид:
|
|
|
Преобразуем выражение 
Для этого введем обозначение 
Получаем 
В последней формуле воспользовались определением полного дифференциала функции многих переменных 
Поле Диполя.
Система, состоящая из двух точечных зарядов разных знаков, находящихся на небольшом расстоянии δr, называется диполем, при этом вектор δr – называют плечом диполя, произведение dp=qδr – элементарным дипольным моментом.
|
элементарный потенциал
поля в точке А, считая, что
δr – бесконечно малая
величина
После несложных
преобразований это
выражение принимает вид:
Для неэлементарного диполя, эти 2 формулы, можно рассматривать, как приближённые для поля на больших расстояниях (т.е. при условии, что плечо диполя много меньше длины радиус вектора |r|)
Дата добавления: 2018-08-06; просмотров: 435; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!