Понятие и определение управляемости линейной стационарной системы
Данное свойство характеризует принципиальную возможность (необходимое условие) перевода вектора состояния системы из одного заданного состояния в другое состояние за конечное время.
Такая возможность существует, если на каждую переменную вектора состояния можно целенаправленно воздействовать с помощью сигнала управления в течение конечного промежутка времени.
В общем случае понятие управляемости имеет отношение к процессу, а не к системе.
Однако, если система линейна и стационарна, то понятие управляемость процесса тождественна понятию - управляемости системы.
Более строгое определение управляемости дано Калманом (управляемость по Калману):
Если для произвольно заданных состояний системы, определяемых значениями вектора состояния 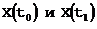 существует вектор U, переводящий систему из одного состояния в другое за время
существует вектор U, переводящий систему из одного состояния в другое за время  ,то система называется вполне управляемой по Калману.
,то система называется вполне управляемой по Калману.
Оценка управляемости системы, описываемой уравнениями состояния метода параллельного программирования
Наиболее просто управляемость оценивается при описании системы уравнениям по методу параллельного программирования (содержат канонический вектор состояния).
Рассмотрим такую модель скалярной системы.
Согласно схеме, на каждую переменную вектора состояния можно воздействовать с помощью сигнала управления, если ни один коэффициент "  " не равен нулю.
" не равен нулю.
При записи уравнений системы в векторно-матричном виде данные коэффициенты являются сомножителями элементов столбца матрицы управления "В". Если хотя бы один коэффициент "  " равен нулю (например, при равенстве постоянных времени
" равен нулю (например, при равенстве постоянных времени  числителя и знаменателя), то переменная
числителя и знаменателя), то переменная  не управляема.
не управляема.
|
|
|
В передаточной функции происходит сокращение нуля и полюса (соответствует понятию вырождения ПФ). Следовательно - вырождение ПФ есть признак потери полной управляемости системы. При этом вектор состояния системы не может быть переведен в заданное состояние.
Если рассматривается модель многомерной системы с каноническим вектором состояния , имеющая  входных воздействий ( второе уравнение состояния при анализе управляемости не требуется):
входных воздействий ( второе уравнение состояния при анализе управляемости не требуется):

матрица системы и матрица управления имеют вид:
A =  B =
B = 
где
n – количество строк - число переменных состояния
m – количество столбцов- число входных воздействий.
Система скалярных уравнений соответствующая матричному уравнению состояния имеет вид:

Откуда следует - сигнал управления не достигает некоторой переменной состояния  , если в соответствующем уравнении будет отсутствовать слагаемое под знаком суммы. Это возможно, только в том случае, когда все элементы соответствующей строки матрицы Вравны нулю. Таким образом, число неуправляемых переменных состояния ( в модели с каноническим вектором состояния) равно числу нулевых строк матрицы В.
, если в соответствующем уравнении будет отсутствовать слагаемое под знаком суммы. Это возможно, только в том случае, когда все элементы соответствующей строки матрицы Вравны нулю. Таким образом, число неуправляемых переменных состояния ( в модели с каноническим вектором состояния) равно числу нулевых строк матрицы В.
|
|
|
Таким образом оценка управляемости (и наблюдаемости) системы при описании ее с помощью канонического вектора состояния является наиболее простой . В этом случае для оценки неуправляемых переменных состояния достаточно определить нулевые строк иматрицы В , а для оценки ненаблюдаемых переменных состояния- нулевые столбцы матрицы С).
26. Принцип двойственности. Оценка управляемости при общей форме записи уравнений состояния
Для решения задачи оценки управляемости в общем случае уравнений состояния используем принцип двойственности (дуальности) линейной системы.
Прежде чем рассмотреть математическое содержание принципа, укажем на следующие соображения, следующие из определения понятий наблюдаемости и управляемости.
1.В частности, рассматривая наблюдаемость и управляемость системы с каноническим вектором состояния, обращаем внимание на определенную симметрию в их оценке. Так, наблюдаемость оценивается по матрице выхода(С), управляемость по матрице входа (В). В первом случае количество ненаблюдаемых переменных равно количеству нулевых столбцов, во втором количество неуправляемых переменных - количеству нулевых строк.
|
|
|
2. При построении замкнутых систем управления (построенных в соответствии с принципом обратной связи) оба свойства (управляемость и наблюдаемость) принципиально важны.
Так, чтобы иметь возможность управлять отдельными переменными состояния необходимо контролировать их изменение, вызванное этим управлением , а для реализации управления необходимы каналы передачи сигала обратной связи к переменным состояния, т.е -необходима управляемость. Таким образом, между данными свойствами по отношению к конечному результату – возможности перевода вектора состояния из какого-то исходного положения в желаемое - существует взаимная связь, выражающаяся в виде их определенной симметрии.
Именно это свойство симметрии и лежит в основе принцип дуальности линейной системы.
Рассмотрим математическое содержание данного свойства
Пусть процессы в системе определяются уравнениями

Этой системе соответствует дуальная система, получаемая из исходной системы в результате применения следующей процедуры:
|
|
|
- обращается время;
-переставляются в общей структуре местами матрица управления (В) и матрица выхода (С ) ;
- производится транспонирование всех матриц ( А,В,С).
Таким образом, уравнения дуальной системы приобретают вид:
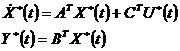
Свойство дуальности выражается в том, что управляемость исходной системы соответствует наблюдаемости двойственной системы и наоборот.
Математически это обеспечивается равенством матрицы управляемости исходной системы матрице наблюдаемости двойственной системы и наоборот. Поскольку выражение для матрицы наблюдаемости было получено в результате математического доказательства , используем это для получения выражения для матрицы управляемости исходной системы
Так, в случае линейной стационарной системы выведено выражение для матрицы наблюдаемости:


Применим его к дуальной системе, заменим в этом выражении матрицы системы в соответствии с процедурой дуальности :

 =N
=N
Полученное выражение определяет матрицу наблюдаемости двойственной системы
и, следовательно, данное выражение равно матрице управляемости исходной системы.
Важными достоинствами свойства дуальности являются следующие :
- результаты преобразований, полученные на основе свойства двойственности , не требуют отдельного математического доказательства, то есть выполнение данного свойства - есть собственно факт такого доказательства;
- принцип двойственности оказывается справедливым и для линейных нестационарных систем, для которых оценка управляемости и наблюдаемости значительно сложнее, чем в стационарной системе;
- поскольку матрицы и управляемости системы входят в выражения для алгоритмов наблюдения и управления систем, то для их вычисления может быть использована одна и та же программа, что существенно экономит объем памяти и число операций вычислителя.
27.Описание движения нестационарной линейной системы
Рассмотрим скалярную линейную нестационарную систему.
Под нестационарной системой будем понимать линейную систему с изменяющимися во времени параметрами. Аналитическое исследование такой системы предполагает выполнение условия, ограничивающего быстроту изменения параметров системы.
В качестве такого ограничения рассматривается следующее условие для импульсно-переходной (весовой) функции системы:
- изменение параметров системы на интервале времени с момента времени возникновения мгновенного импульса и до окончания реакции на него практически не влияет на вид этой реакции, то есть - весовая функция системы определяется только состоянием параметров системы в момент времени возникновения мгновенного импульса
В качестве примера, рассмотрим скалярную нестационарную систему.
Поскольку параметры системы в каждый момент времени различны, то в зависимости от момента времени возникновения мгновенного импульса весовая функция будет иметь также различный вид. Поэтому выражение для весовой функции такой нестационарной системы должно содержать два аргумента :
- текущее время (t),отсчитываемое от момента включения системы (начало отсчета времени) до момента наблюдения реакции;
- «параметрическое» время (  ), отсчитываемое от момента времени включения системы до момента времени возникновения мгновенного импульса. В общем виде выражение для такой весовой функции имеет вид:
), отсчитываемое от момента времени включения системы до момента времени возникновения мгновенного импульса. В общем виде выражение для такой весовой функции имеет вид:

где
 -текущее время, отсчитываемое от момента возникновения мгновенного импульса до момента времени наблюдения реакции.
-текущее время, отсчитываемое от момента возникновения мгновенного импульса до момента времени наблюдения реакции.
При введении параметрического времени весовая функция рассматриваемой нестационарной системы может быть записана в виде:

Иллюстрация приведена на Рис.4.15.
Заметим, что в линейной стационарной системе весовая функция от момента времени возникновения импульса не зависит - ее текущее значение определяется только одним аргументом  ( зависит только от интервала времени, а не от его начала). Если момент отсчета текущего времени совпадает с моментом возникновения импульса, то приходим к известному ранее выражению:
( зависит только от интервала времени, а не от его начала). Если момент отсчета текущего времени совпадает с моментом возникновения импульса, то приходим к известному ранее выражению:

Выражение весовой функции геометрически задает поверхность.
Сечения этой поверхности для различных (фиксированных) значений параметрического времени  приведены на Рис.4.16.
приведены на Рис.4.16.
Функции в этих сечениях могут начинаться только на прямой  , так как раньше, чем появляется воздействие (мгновенный импульс), реакция возникнуть не может(условие физического существования). Такие функции называют нормальными весовыми функциями.
, так как раньше, чем появляется воздействие (мгновенный импульс), реакция возникнуть не может(условие физического существования). Такие функции называют нормальными весовыми функциями.
Если зафиксировать время наблюдения (t) и рассмотреть сечение поверхности плоскостью перпендикулярной оси текущего времени, то значения ординат поверхности в рассматриваемом сечении определяют вклад вносимый нормальными весовыми функциями в функцию данного сечения
Весовые функции в рассматриваемом сечении называют сопряженными весовыми функциями.
Аргументом сопряженной весовой функции является параметрическое время"  "
"
Зависимость выходной переменной от произвольного воздействия для текущего момента времени наблюдения реакции определяется именно сопряженной весовой функцией.

Рассмотрим многомерную линейную нестационарную систему.
Уравнения состояния нестационарной системы в пространстве состояний записываются в виде:


Показано (Заде.Л, Дезоер.Ч. Теория линейных систем. Метод пространства состояний.М,Наука,1970г),что решение этих уравнений записывается в виде:
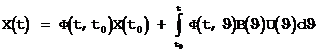
где
 момент времени начала движения.
момент времени начала движения.
Вектор выхода определяется выражением:
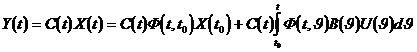
Матрица Коши нестационарной системы удовлетворяет условию фундаментальной матрицы:

Свойства и определение фундаментальной матрицы нестационарной системы
Элементами этой матрицы являются, выше рассмотренные ,сопряженные весовые функции линейной нестационарной системы
Для фундаментальной матрицы нестационарной системы справедливы следующие соотношения:
1. 
2. 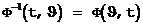
3. 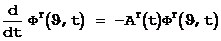

Заметим, что фундаментальная матрица нестационарной системы (в отличие от стационарной) редко может быть выражена с помощью элементарных функций, в связи с чем приходится использовать методы численного интегрирования( например метод Пикара).
Согласно этому методу решение нестационарного линейного матричного уравнения:


где

Данный бесконечный функциональный ряд в общем случае сходится медленно. Кроме того, его вычисление сопряжено с трудоемкими выкладками, так как помимо последовательного интегрирования приходится многократно перемножать матрицы высокого порядка.
Весовая матрица нестационарной линейной системы имеет вид:

 элемент матрицы представляет реакцию в момент t i-ой компоненты вектора выхода на импульс j-ой компоненты вектора входа, приложенный в момент времени
элемент матрицы представляет реакцию в момент t i-ой компоненты вектора выхода на импульс j-ой компоненты вектора входа, приложенный в момент времени 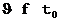 при нулевых начальных условиях в момент
при нулевых начальных условиях в момент  .
.
Матрица переходных функций определяется выражением:

Дата добавления: 2018-08-06; просмотров: 455; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
