Получение общего решения уравнений состояния линейной многомерной стационарной системы.
Математическое решение этой задачи связано с решением уравнений состояния.
В 1969 году Р. Беллманом доказано, что общее решение векторно-матричного уравнения состояния линейной системы управления по форме аналогично решению скалярного дифференциального уравнения первого порядка. Воспользуемся данной аналогией.
Рассмотрим решение этого уравнения.
Линейная стационарная система первого порядка описывается уравнением вида:
Здесь
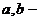коэффициенты, являющиеся алгебраическими величинами.
При ненулевых начальных условиях преобразование по Лапласу данного уравнения имеет вид:
Разрешая его относительно изображения переменной состояния 
,получаем:
Возьмем обратное преобразование Лапласа, воспользовавшись формулой соответствия:
и свойством преобразования Лапласа:
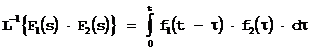
Получаем: 
Первое слагаемое определяет свободное движение системы (движение обусловленное ненулевыми начальными условиями - "начальными возмущениями" ).
Это движение соответствует общему решению дифференциального уравнения (его иногда называют фундаментальным решением). Как известно,характер этого движения определяет понятие устойчивости процесса.
Второе слагаемое соответствует вынужденному движению системы и причиной его является воздействие 
, имеющее произвольный вид.
При нулевых начальных условиях получаем связь переменных "вход-выход", рассмотренную ранее в разделе классической ТАУ:
|
|
|
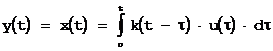
где 
- весовая функция скалярной системы
Фундаментальная матрица системы
Фундаментальная матрица системы и некоторые способы ее определения
Матричный экспоненциал 
называют матрицей Коши и обозначают 
. Это функциональная матрица аргумента 
(времени).
Данная матрица удовлетворяет математическому определению фундаментальной матрицы:
Ее принято называть фундаментальной матрицей системы (матрица Коши является частным случаем более широкого понятия - фундаментальная матрица).
В развернутом виде первое слагаемое решения векторно-матричного уравнения состояния имеет вид:
= 
Рассмотрим одну их составляющих вектора состояния:
Согласно данному выражению некоторая переменная вектора состояния в свободном движении равна сумме, реакций отдельных переменных состояния системы на типовые воздействиями в виде «начальных импульсных возмущений » - начальных условий )
Полная аналогия с характеристиками скалярной системы "вход -выход" соответствует выражению ( с учетом второго уравнения состояния):
При нулевых начальных условиях получаем ( по аналогии с классической теорией управления ) весовую и переходную матрицы многомерной системы:
|
|
|
K 
; 
Как показывает решение уравнений состояния и характеристики динамики в области времени – ядром динамики процесса системы управления является фундаментальная матрица системы.
Рассмотрим некоторые способы определения фундаментальной матрицы для общего случая описания системы в пространстве состояний
Непосредственный способ определения фундаментальной матрицы
Этот способ дает аналитическое описание фундаментальной матрицы и ориентирован на системы невысокого порядка. Использует операцию обращения матрицы.
Преобразование Лапласа решения уравнение свободного движения имеет вид:
где
изображение Лапласа фундаментальной матрицы системы ( резольвента матрицы А).
Поэтому непосредственный способ определения фундаментальной матрицы состоит в получении обратного преобразования Лапласа от обратной матрицы:
Таким образом процедура определения фундаментальной матрицы по данному способу сводится к процедуре обращения матрицы, а именно:
- образование на основе известной матрицы системы ( А )
матрицы вида ;
- транспонирование матрицы ,
-замена каждого элемента транспонированной матрицы алгебраическим дополнением,
|
|
|
-расчет определителя матрицы,
-деление алгебраического дополнения на определитель матрицы;
- взятие обратного преобразования Лапласа от каждого элемента обратной матрицы.
Именно в связи с неэкономичностью ( в смысле вычислительных затрат) операции обращения матрицы, алгоритм используется для систем невысокого порядка и предназначен для изучения динамических свойств по аналитическим выражениям.
Заметим, что программная реализация операции обращения матрицы требует почти в три раза больше операций и два раза больше памяти, чем интегрирование линейной системы уравнений. Операции обращения по возможности следует исключать из вычислений.
Способ разложения в ряд матричного экспоненциала.
Описание фундаментальной матрицы в области времени представляет матричную функцию (матричный экспоненциал), разложение которой в ряд имеет вид:
Существенно, что расчет может проводиться для любого заданного момента времени (предшествующие значения можно не определять). Поскольку ряд быстро сходится, то для расчета достаточно нескольких первых членов. Алгоритм широко применяется на практике для систем высокого порядка.
Получение фундаментальной матрицы по метод Фаддеева
|
|
|
(Фаддеев Д.К, Фаддеева В.Н. Вычислительные методы линейной алгебры 1960г.)
Метод следует из теоремы Леверье. Согласно методу, изображение Лапласа фундаментальной матрицы стационарной системы тождественно выражению:
где
матрицы, размера( 
)вычисляемые по рекурентным выражениям.
коэффициенты (скалярные величины).
Процедура определения матриц 
:
Коэффициенты 
определяются через сумму диагональных элементов (следов) матриц по формулам:
Последовательность вычислений:
-расчет коэффициента 
, матрицы 
, коэффициента 
, матрицы 
и так далее до полного определения всех матриц;
-суммирование матриц числителя;
- деление всех элементов суммарной матрицы числителя на полином знаменателя выражения;
- получение обратного преобразования Лапласа от каждого элемента последней матрицы.
В качестве контроля при расчете матриц 
используется уравнение:
Точность численных расчетов можно определить по ненулевым элементам данной матрицы. Как видно алгоритм исключает операцию обращения матрицы, что и является его достоинством. Удобен для реализации на ЭВМ. Чувствителен к ошибкам округления. Существует вычислительная программа на Фортране (1970 г.)
Дата добавления: 2018-08-06; просмотров: 417; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!