Векторно-матричная структура многомерной следящей системы. Матричные передаточные функции. Анализ устойчивости многомерной системы.
Рассмотрим структурное представление уравнений состояния:
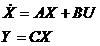
Выполним преобразование Лапласа при ненулевых начальных условиях:
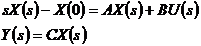
Перейдем от аргумента преобразования Лапласа к оператору дифференцирования и введем графический символ интеграла от вектора:
Отобразим алгебраическую связь между векторами в виде структурной схемы (Рис.4.10):
В этой схеме знак векторной связи положительный. Заметим, что в отличие от скалярной схемы, знак векторной обратной связи не принципиален. Отдельные составляющие этой связи могут иметь различные знаки (коэффициенты матрицы). В общем случае знак векторной связи зависит от знака перед матрицей в уравнении состояния.
Рассмотрим нулевые начальные условия и разрешим преобразованные по Лапласу уравнения относительно изображения вектора состояния:
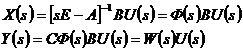
Оператор связи между изображениями вектора управления и вектора выхода по аналогии со скалярной системой называют матричной передаточной функцией.
В отличие от скалярной системы при ее образовании важен порядок перемножения составляющих матриц. Это связано с тем, что произведение матриц операция некоммутативная.
Матричная передаточная функция содержит элементы, каждый из которых представляет скалярную передаточную функцию, связывающую отдельное скалярное воздействие с выходной скалярной координатой. Скалярная структурная схема системы с тремя входами и выходами , соответствующая матричной передаточной функции вида,
|
|
|
изображена на Рис.4.11
Если матрица является диагональной, то в системе отсутствуют перекрестные взаимные связи между основными каналами управления. Такие каналы управления называется автономными..
Матричные передаточные функции многомерной следящей системы
Дополним, полученное выше, выражение матрицей, преобразующей вектор ошибки слежения в сигнал управления:
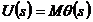
Векторная структура следящей системы имеет вид, показанный на Рис.4.12.
Матричная ПФ разомкнутой многомерной системы представляется в виде:
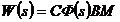
Получим остальные МПФ многомерной следящей системы.
Уравнения, согласно векторно-матричной структурной схеме, имеют вид:
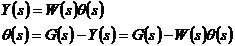
Разрешая уравнение относительно изображений векторов ошибки и входного воздействия, получаем векторное уравнение ошибки :
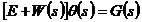
Здесь, выражение
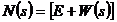является характеристической матрицей замкнутой многомерной системы.
Равенство нулю определителя этой матрицы (условие вырождения матрицы)
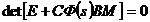
приводит к характеристическому (алгебраическому) уравнению замкнутой многомерной следящей системы.
Исследование этого характеристического уравнения (знаки и топология корней уравнения , анализ соотношений между коэффициентами – применение алгебраических критериев устойчивости ) ) позволяет получить представление о поведении свободного движения многомерной системы и широко используется при исследовании устойчивости линейных многосвязных многомерных систем высокого порядка
|
|
|
Из уравнения для вектора ошибки следует выражение для МПФ ошибки:
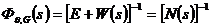
Таким образом, матричная ПФ ошибки многомерной следящей системы есть обратная (обращенная) характеристическая матрица системы.
Если подставить выражение для вектора ошибки в первое уравнение динамики, то получаем выражение для МПФ следящей системы, связывающей вектор ее входа и вектор ее выхода.
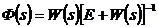
При составлении выражений для МПФ следует иметь в виду, что порядок записи матриц при преобразовании вектора, соответствует умножению слева на матрицу, преобразующую вектор.
Дата добавления: 2018-08-06; просмотров: 486; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!