Процедура метода прямого программирования
В теории аналогового и цифрового моделирования является основой метода прямого программирования. Реализуется в двух формах. Рассмотрим первый вариант этой схемы (первая каноническая форма) для скалярной системы с невырожденной ПФ вида:
Поделив числитель и знаменатель на 
, перепишем полиномы числителя и знаменателя ПФ в обратной последовательности и вынесем коэффициент 
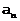за скобки знаменателя:
Введем новую переменную 
,определяемую выражением:
Сохраним левую часть уравнения без изменения, а правую перепишем в виде алгебраического уравнения:
Полученное уравнение дополним его вторым уравнением, связывающим переменную Е и ее производные с выходной переменной системы :
По данным уравнения построим структурную схему и для введения начальных условий и заменим переменную преобразования Лапласа «s» наоператор дифференцирования «р»:
Рассмотрим в качестве переменных состояния выходные координаты интегрирующих звеньев полученной схемы , начиная нумерацию их с выхода. Введем начальные условия по всем переменным, приведя их к выходным переменным интеграторов ( в виде масштабированных единичных функций) (Рис.4.3).
Особенности схемы :
1. Число интеграторов равно порядку полинома знаменателя невырожденной ПФ (порядку дифференциального уравнения) и, соответственно, числу переменных состояния;
2. Переменные состояния в общем случае не являются производными выходной переменной системы
|
|
|
3. Схема содержит внутренние обратные связи по переменным состояния, число которых равно порядку системы. Данные связи формируют знаменатель ПФ и, следовательно, определяют характер свободного движения системы -устойчивость системы. При условии, когда 
, схема моделирует свободное движение системы, в этом случае переменные состояния соответствуют нормальной форме Коши (производные выходной координаты).
4 . Элемент фундаментальной матрицы определяется по данной структурной схеме в виде реакции на конкретное начальное возмущение
По схеме записываем уравнения состояния:
.......
Построенная по этому уравнению матрица коэффициентов системы, является матрицей Фробениуса:
A = 
Второе уравнение состояния, получаемое по схеме в переменных состояния, имеет вид:
Заменяя последнюю переменную в уравнении на последнее уравнение в выше приведенной системе уравнений Коши,
получаем:
Таким образом, согласно последнему уравнению матрица выхода системы имеет одну строку, определяемую коэффициентами этого уравнения.
Общее форма записи уравнений состояния имеет вид:
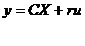
где
u, y - скалярные переменные
|
|
|
r - коэффициент передачи (существует при равенстве порядков полиномов числителя и знаменателя ПФ ).
Важное достоинства такой записи уравнений состояния в такой форме в том, что при организации вычислительной процедуры интегрирования уравнений, не требуется информации о производных воздействия ( в отличие от выше рассмотренной непосредственной формы записи в нормальной форме Коши).
При определении фундаментальной матрицы по схеме в переменных состояния следует приравнять все коэффициенты числителя ПФ нулю ( 
) и с помощью структурных преобразований определить ПФ между начальными возмущениями (поочередно) и переменными состояния. Затем необходимо взять обратное преобразование Лапласа от каждого из полученных выражений:
= 
Рассмотрим типовые звенья и их простейшие соединения в пространстве состояния, получаемые согласно первой форме метода прямого программирования.
Пример 2. Колебательное звено
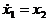
Дата добавления: 2018-08-06; просмотров: 332; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!