Двухканальная система с комбинированным управлением и ее новые возможности.
Многоканальные итерационные системы с комбинированным управлением
В основном применяются при построении высокоточных измерительных систем.
Система конструктивно содержит только один дискриминатор ошибки, имеющий большую линейную зону статической характеристики. Он осуществляет замыкание подсистемы грубого канала (Рис.3.98). Перейдем от структуры двухканальной системы с комбинированным управлением к рассматриваемой системе:
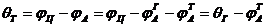
Согласно полученному выражению в таком объединении подсистем, ошибка боле широкополосной подсистемы определяется как разность между ошибкой грубого канала и выходной переменной точного канала при последующем суммировании их выходных углов поворота. Подсистема точного канала замыкается с помощью отдельного датчика по своей собственной координате.
Такая схема объединения подсистем может быть распространена на любое количество каналов. При этом , каждый дополнительный канал уменьшает ошибку системы в целом.
Существенный недостаток такой технической реализации системы связан с реализацией процедуры замыкания точного канала с помощью отдельного датчика относительного угла. Погрешности этого датчика не охватываются обратной связью и входят непосредственно в ошибку системы в целом. Предъявляются особые требования к его точности.
В большинстве применений таких объединений (измерительные комплексы) моменты инерций каналов существенно отличаются ( больше, чем в 10 раз) . Это позволяет считать взаимные связи малыми и, соответственно, рассчитывать подсистемы как независимые.
|
|
|
При использовании такой структуры в прецизионных системах автосопровождения , работающих на подвижном основании, динамическая ошибка от входного воздействия и особенно ошибка от качки основания существенно увеличиваются при наличии запаздывания в дискриминаторе ошибки (например при использовании цифровой обработке изображения проекции цели в приемнике оптической энергии).
Вектор состояния и его координаты. Уравнения состояния (получения матриц уравнений состояния в форме Фробениуса)
В случае трехмерного (геометрического) пространства (n=3), метрика определяет расстояние (отрезок прямой) между двумя точками (состояниями), являющимися концами двух радиус-векторов (Рис.4.1). При движении системы в таком пространстве конец этого вектора, описывает пространственную кривую (траекторию). Ее называют фазовой траекторией , а сам вектор – вектором состояния или фазовым вектором. Если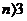 
, то понятия геометрического пространства не существует , сохраняется понятие многомерного пространства.
|
|
|
Основные положения метода пространства состояния
1. Элементу пространства состояния соответствует значение вектора состояния в конкретный момент времени. Координаты такого вектора принято называть фазовыми координатами или переменными состояния. В дальнейшем используем термин –переменные состояния. На рис.1 такими переменными являются координаты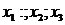 
2. Переменные состояния это независимые координаты системы ( не могут быть выражены через линейную комбинацию других переменных состояния).
Если система описывается дифференциальными уравнениями, то это количество равно порядку этого уравнения.
Количество координат вектора состояния является минимально-необходимым для того, чтобы можно было описать поведение системы при известных начальных условиях и воздействиях.
Важно, что при формировании модели системы переменные состояния совершенно необязательно должны быть физически реальными переменными системы. Такая формализация позволяет широко использовать при исследовании модели векторно-матричный аппарат, что делает описание более компактным. Это особенно существенно при исследовании динамики сложных (многомерных и многосвязных ) систем.
3. Пространство состояний системы, взаимодействующей с окружающей средой, дополняется множествами входных и выходных переменных, что позволяет рассмотреть модель системы в виде математического образа, который в теории управления получил название " черного ящика" (Рис.4.2).
|
|
|
В данном математическом отображении системы принимаются следующие обозначения:
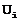- совокупность входных переменных (входные каналы),генерируемая системами внешними по отношению к исследуемой;
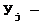совокупность выходных переменных (выходные каналы),представляющих реакции системы на воздействия (управляющие и возмущающие);
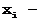внутренние переменные (переменные состояния, фазовые координаты,) относятся к содержимому "черного ящика" и скрыты от наблюдателя (именно поэтому он и называется "черным").
Уравнения состояния линейной стационарной системы
Поставим в соответствие переменным принятой модели в виде "черного" ящика следующие обозначения:
Вектор входа
U=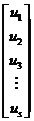 
s- количество входов
Вектор выхода
Y= 
j- количество выходов
Вектор состояния (фазовый вектор)
Х=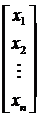 
n- количество переменных состояния
Можно показать ,что если система линейна и стационарна, то ее исходные уравнения, полученные по физическим моделям элементов, всегда можно преобразовать к двум векторно-матричным уравнениям, называемым уравнениями состояния:
|
|
|
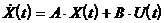
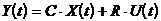
где
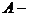матрица системы (коэффициентов системы);
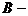матрица управления (коэффициентов управления);
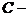матрица выхода
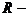матрица усиления.
Переход от передаточной функции к уравнениям состояния в нормальной форме Коши
Для примера рассмотрим непосредственный переход от ПФ скалярной системы у уравнениям состояния в нормальной форме Коши.Пусть данная передаточная функция невырождена ( то есть –полностью и однозначно отображает исходное дифференциальное уравнение системы).
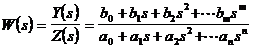
Перейдем к уравнению, в котором левая часть переписана в обратном порядке:
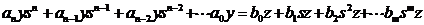
Представим правую часть уравнения в виде скалярной входной переменной ,
представляющая линейную комбинацию производных входного воздействия.
u =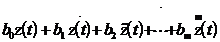 
Используя обратное преобразование Лапласа перейдем к дифференциальному уравнению системы :
,
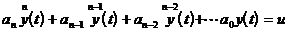Выберем переменные состояния (фазовые координаты).
В качестве этих переменных в системе управления удобно выбрать производные выходной переменной. Как известно в математике , такой способ выбора переменных состояния приводит к системе уравнений в нормальной форме Коши (процедура Коши).
Согласно данной процедуре первая переменная состояния принимается равной выходной переменной системы , а последняя переменная состояния равна (n-1)-ой производной выходной переменной.
Согласно данной процедуре получаем:
; 
; 
; ... 
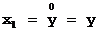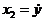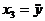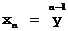
После введения переменных состояния диф. уравнение записывается в виде:
,
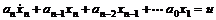Запишем приведенные выше уравнения в виде системы уравнений , в левой части которых находятся первые производные переменных состояния :
......
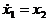
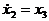
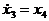
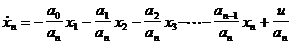
Заметим, что сигнал управления в скалярной системе непосредственно воздействует на высшую производную системы.
Левая часть системы уравнений представляет содержит производные переменных состояния. Правая часть представляет функции от собственно переменных состояния и входных воздействий. Данная функция является их линейной комбинацией.
Перейдем от системы уравнений в форме Коши , к векторно-матричной форме.
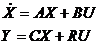
Для этого исследуем такой переход по частям
Рассмотрим первое слагаемое первого уравнения состояния
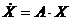
Математически векторы X и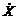 
вектор состояния и его производная) , отображаются в виде матриц-столбца
Для получения матрицы А уравнения переписываются в виде, который является результатом произведения матрицы- столбца на некоторую матрицу (это матрица А):
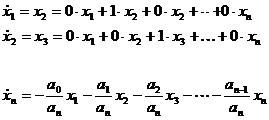
Откуда получаем описание матрицы коэффициентов системы уравнений имеет вид
A =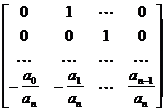 
Такая форма матрицы называется матрицей Фробениуса. Если уравнения системы содержат такую матрицу их называют уравнениями состояния в форме Фробениуса.
Дата добавления: 2018-08-06; просмотров: 726; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!