Анализ устойчивости с помощью алгебраических критериев.
Алгебраические критерии устойчивости состоят в использовании коэффициентов характеристического уравнения. Если для систем 1-го и 2-го порядка (порядок не превышает 2(характеристического уравнения)) все коэффициенты > 0, то система является устойчивой.
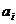 >0;
>0; 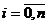 ;
; 
Для  это условие является необходимым, но не достаточным. В этом случае из коэффициентов характеристического уравнения составляем матрицу Гурвица, например для n=5.
это условие является необходимым, но не достаточным. В этом случае из коэффициентов характеристического уравнения составляем матрицу Гурвица, например для n=5.
Правило: по главной диагонали записывают коэффициенты от  до
до 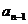 . Затем в строках
. Затем в строках
 записывают коэффициенты в порядке возрастания индексов. Если индекс > n и <0 , то в строке ставят 0. После составления матрицы вычисляют определители Гурвица.
записывают коэффициенты в порядке возрастания индексов. Если индекс > n и <0 , то в строке ставят 0. После составления матрицы вычисляют определители Гурвица.
 ;
;  ;
;  и т.д.
и т.д.  ,
,  .
.
При этом, 
Если  > 0 то
> 0 то  определяется
определяется  .
.
Необходимым и достаточным условием является положительность всех определителей Гурвица. Если хотя бы один из них отрицательный – система не устойчива. Система находиться на границе устойчивости, если n-й определитель равен 0, в этом случае мы можем уменьшив  (
(  ) обеспечив устойчивость.
) обеспечив устойчивость.
Плюс метода: простота.
Минус метода: метод не отвечает как обеспечить устойчивость (как изменить параметры системы, для обеспечения устойчивости); нельзя определить запас устойчивости.
Этот метод можно применять для замкнутых систем.
Частотные критерии устойчивости (Найквиста и Михайлова).
К ним относятся критерий Михайлова и Найквиста, исследование по ЛАЧХ.
Критерий Михайлова
Исследуется характеристический комплекс замкнутой системы. Его можно определить следующим образом:
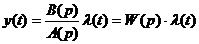 - ДУ
- ДУ
 , - характеристическое уравнение.
, - характеристическое уравнение.
 ;
;
Заменим S на  и получим характеристический комплекс:
и получим характеристический комплекс:
 (1).
(1).
Характеристический комплекс образуется приравниванием знаменателя ПФ замкнутой системы к 0 и заменой р на  . Характеристический комплекс это вектор. Критерий основан на исследовании аргумента характеристического комплекса.
. Характеристический комплекс это вектор. Критерий основан на исследовании аргумента характеристического комплекса.
При изменении 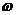 от
от  до
до  угол поворота этого вектора приобретает приращение. Угол приращения определяется порядком и устойчивостью системы. Если при изменении
угол поворота этого вектора приобретает приращение. Угол приращения определяется порядком и устойчивостью системы. Если при изменении 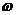 от
от  до
до 
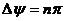 то система является устойчивой. Если
то система является устойчивой. Если  <
< 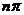 то система неустойчива. Практически: разделим характеристический комплекс на действительную и мнимую части, действительная содержит четные номера.
то система неустойчива. Практически: разделим характеристический комплекс на действительную и мнимую части, действительная содержит четные номера.
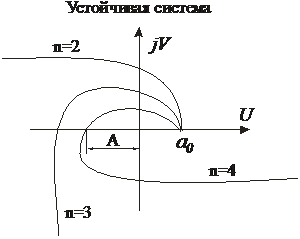
Пусть n=6: 
Мнимая: 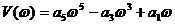
 Очевидно, что характеристический комплекс при определении его 1/n с изменяющеюся частотой. А в общем конец вектора прочерчивает кривую называемую годографом:
Очевидно, что характеристический комплекс при определении его 1/n с изменяющеюся частотой. А в общем конец вектора прочерчивает кривую называемую годографом:
 - содержит четные степени. При изменении
- содержит четные степени. При изменении  система будет устойчива, если
система будет устойчива, если  и не устойчива, если
и не устойчива, если  .
.
 Критерий: если годограф характеристического комплекса при изменении
Критерий: если годограф характеристического комплекса при изменении  от 0 до
от 0 до  последовательно проходит n квадрантов, система является устойчивой; если последовательность нарушается, то система не устойчива.
последовательно проходит n квадрантов, система является устойчивой; если последовательность нарушается, то система не устойчива.
Если годограф проходит через ноль координатной плоскости система находится на границе устойчивости.
 Находим значения частот при которых Im XK = 0 ; и последовательно подставим эти частоты в Re XK. Если эти корни перемежаются для Im Re: действительная часть последовательно меняет свой знак, то система устойчива; если не перемежаются, то система неустойчива.
Находим значения частот при которых Im XK = 0 ; и последовательно подставим эти частоты в Re XK. Если эти корни перемежаются для Im Re: действительная часть последовательно меняет свой знак, то система устойчива; если не перемежаются, то система неустойчива.
 при росте
при росте  .
.
Поскольку в замкнутой системе все передаточные функции имеют один и тот же знаменатель, то для определения устойчивости можно взять любую переходную функцию.
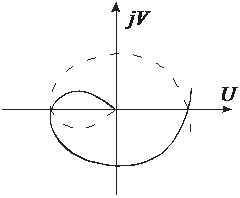
Когда  (
(  ), то при каком-то
), то при каком-то  годограф может пройти через ноль координатной плоскости из-за сдвига вправо.
годограф может пройти через ноль координатной плоскости из-за сдвига вправо.
Поэтому А (смотри Рис.) определяет запас устойчивости по ???.
Критерий Найквиста
Основан на исследовании ПФ разомкнутой системы.

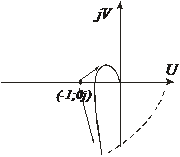 Если годограф частотной ПФ разомкнутой системы, устойчивой в разомкнутом состоянии не охватывает точку с координатами (-1;0j) , то система является устойчивой (при изменении
Если годограф частотной ПФ разомкнутой системы, устойчивой в разомкнутом состоянии не охватывает точку с координатами (-1;0j) , то система является устойчивой (при изменении  от 0 до
от 0 до  ) в замкнутой системе; если охватывает, система неустойчива в замкнутом состоянии. Если годограф проходит через координаты (-1;0j) , то система на границе устойчивости.
) в замкнутой системе; если охватывает, система неустойчива в замкнутом состоянии. Если годограф проходит через координаты (-1;0j) , то система на границе устойчивости.
Для некоторых систем годограф может уходить в «бесконечность». Тогда чтобы использовать правило, из точки на Re оси радиус до пересечения с годографом.
Это делают для того, чтобы: проведя векторы из точки к годографу, и если при изменении частоты полное приращение угла поворота равно 0, то годограф не охватывает точку.
 Если кривая проходит через (-1;0j) ; то на какой-то частоте,
Если кривая проходит через (-1;0j) ; то на какой-то частоте,  =1 и сдвиг по фазе =
=1 и сдвиг по фазе = 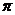 . Если мы теперь замкнём ??? (еще на
. Если мы теперь замкнём ??? (еще на 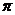 сдвиг), то мы получим условие генерации.
сдвиг), то мы получим условие генерации.
Плюсы способа:
С помощью годографа можно определить запас устойчивости по амплитуде и фазе.


 запас фазы:
запас фазы: 
 - угол, на который надо увеличить запаздывание в системе, чтобы она находилась на границе устойчивости.
- угол, на который надо увеличить запаздывание в системе, чтобы она находилась на границе устойчивости.
Запас устойчивости по амплитуде:  , где
, где 
-позволяет определить пути обеспечения устойчивости.
Дата добавления: 2018-08-06; просмотров: 303; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
