Передаточная функция следящей системы. Переходная и весовая функции.
Переходной функцией называют реакцию системы на ступенчатую единичную функцию:
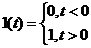
Переходная функция используется при исследовании переходных режимов систем. Переходная характеристика – графическое изображение передаточной функции.
Устойчивые системы

Неустойчивые системы
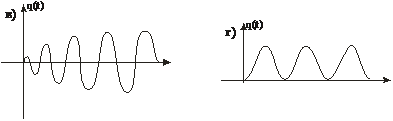
Переходная характеристика может быть найдена аналитически:
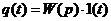 , где W(p) – операторный коэффициент передачи.
, где W(p) – операторный коэффициент передачи.
Перейдя в область изображений по Лапласу, мы получим следующие выражения:
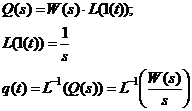
Весовая функция (импульсная характеристика) – реакция системы на воздействие в виде δ-функции:


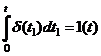 - фильтрующее свойство.
- фильтрующее свойство. 
Весовая функция обозначается как h(t):
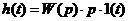
Переходя в область изображений, мы получим следующие выражения:

Весовая и передаточная функции связаны преобразование Лапласа.
Весовая функция используется для определения выходной величины с помощью интеграла Дюамеля. Интеграл Дюамеля записывается следующим образом:
 (*)
(*)
Т.к. существует условие физической реализуемости: функция появляется не раньше воздействия. Соответственно:
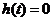 , при t<0.
, при t<0.
Тогда можно записать следующее:
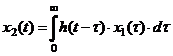
Для определения установившегося значения можно полагать, что воздействие началось в момент 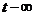 :
:

Существую частные методы исследования системы с использованием частной передаточной функции и частотно-логарифмической характеристики.
|
|
|
Частотная функция определяет реакцию системы на гармоническое входное воздействие.
Частная передаточная функция – это отклонение комплексных амплитуд входных и выходных величин.
W(jω) можно получить формально из W(s), заменой s на jω.
Тогда W(jω)можно записать в виде:


Часто обозначают: 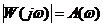
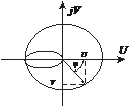
Графическое изображение W(jω) на комплексной плоскости называется амплитудно-фазовой характеристикой:
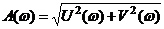 – АЧХ.
– АЧХ.
АЧХ – зависимость амплитуды выходного сигнала от частоты, при неизменной амплитуде входного сигнала.
Выражение для ФЧХ записывается:

ФЧХ – определяет зависимость фазового запаздывания выходного сигнала по отношению к входному от частоты. Она симметрично относительно начала координат.
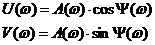
Годограф – кривая, прочерчиваемая концом вектора, при изменении частоты ω на промежутке ( 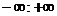 ).
).
Частотная передаточная функция. АФЧХ.
Частотная передаточная функция (комплексный коэффициент передачи) определяет реакцию системы на гармоническое входное воздействие и используется для анализа следящих систем. Ее можно найти, используя ДУ (3.1), если полагать, что  – гармоническое воздействие в комплексной форме определяется выражением
– гармоническое воздействие в комплексной форме определяется выражением
|
|
|
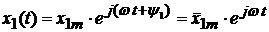 , (3.5)
, (3.5)
где  - комплексная амплитуда.
- комплексная амплитуда.
Будем искать частное решение неоднородного ДУ (1) в виде:
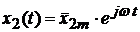 , (3.6) где
, (3.6) где  . Подставляя (3.5), (3.6) в (3.1) и учитывая, что
. Подставляя (3.5), (3.6) в (3.1) и учитывая, что 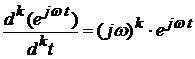 , получим:
, получим:
 ,
,
где 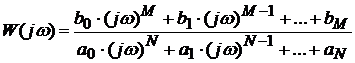 ─ частотная передаточная функция (комплексный коэффициент передачи).
─ частотная передаточная функция (комплексный коэффициент передачи).
Частная передаточная функция – это отношение комплексных амплитуд входных и выходных гармонических воздействий при нулевых начальных условиях.
W(jω) можно получить формально из W(s), заменой s на jω.
W(jω)можно представить а показательной и алгебраической форме:


 - модуль частотной передаточной функции.
- модуль частотной передаточной функции.
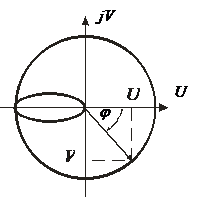 W(jω) на комплексной плоскости изображается в виде вектора. При изменении частоты в интервале (
W(jω) на комплексной плоскости изображается в виде вектора. При изменении частоты в интервале ( 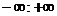 ) конец вектора прочерчивает кривую, называемую амплитудно-фазовой характеристикой (АФХ) (рис. 3.3).
) конец вектора прочерчивает кривую, называемую амплитудно-фазовой характеристикой (АФХ) (рис. 3.3).
Рис. 3.3. Амплитудно-фазовая характеристика
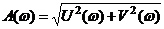 – (АЧХ).
– (АЧХ).
АЧХ – зависимость амплитуды выходного сигнала от частоты при неизменной амплитуде входного сигнала.
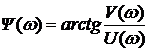 ─ ФЧХ
─ ФЧХ
ФЧХ определяет зависимость фазового сдвига выходного сигнала относительно входного от частоты. Она симметрично относительно начала координат.
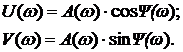
Годограф – кривая, прочерчиваемая концом вектора, при изменении частоты ω в интервале ( 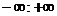 ).
).
|
|
|
ЛЧХ. Примеры построения.
Наиболее удобный для синтеза метод – метод с использованием логарифмических частотных характеристик. Метод состоит в графическом построении АЧХ и ФЧХ в логарифмическом масштабе. Особенно удобен метод, использующий асимптотический ЛАЧХ. Для некоторых систем, достаточно строить лишь ЛАХ. Для таких систем полиномы числителя и знаменателя имеют с отрицательной вещественной частью.
 , где P(jω) = 0; Q(jω) = 0.
, где P(jω) = 0; Q(jω) = 0.
Метод построения асимптотических ЛАХ:

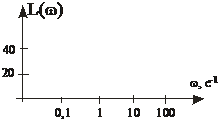
Пример построения асимптотических ЛАХ.


где Т1, Т2, Т3 – постоянные времени соответствующих звеньев; К – коэффициент усиления или добротность (имеет размерность частоты).
А(ω) – модуль для последовательно включенных звеньев. Определяется как произведение модулей; а фаза – как сумма.


обычно полагают, что 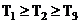 , мы же возьмем Т1 > Т2, > Т3.
, мы же возьмем Т1 > Т2, > Т3.
Обозначим 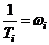 – сопрягающая частота;
– сопрягающая частота; 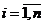

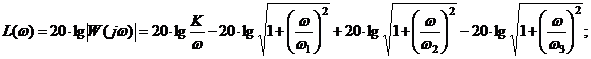
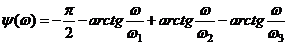 ;
;
При построении асимптоты ЛАХ используется следующее правило:
Если 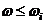 , то
, то 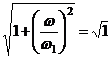 Если
Если  , то
, то 
При этом, в точке сопряжения ошибка порядка несколько дБ.
Асимптотическая ЛАХ для n последовательно включенных звеньев составляет n+1 асимптоту, каждая из которых строится в диапазоне частот:
|
|
|
1ая: 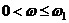
2ая: 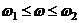
… … … … …
n+1: 
Построим L(ω).
 1ая асимптота (
1ая асимптота ( 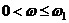 ):
):

при ω = K, L(ω) = 0;
Наклон асимптоты будет равен –20 дБ на декаду.
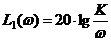
2ая асимптота ( 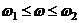 ):
):

Наклон асимптоты будет равен –40 дБ на декаду.

3ья асимптота ( 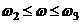 ):
): 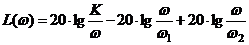
Это уравнение прямой, проходящей через точки L2(ω) и L3(ω).
Где 
Т.о. можно записать: 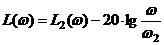
В точке L2 асимптота изменяет свой наклон на +20 дБ, итоговый наклон третьей асимптоты составляет –20 дБ.
4ая асимптота (  ):
):
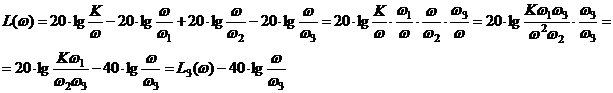
Т.е. при переходе через сопрягающую частоту ω3 асимптота меняет свой наклон на –20 дБ, и в итоге 4ая асимптота наклонена на –40 дБ.
При переходе через очередное значение сопрягающей частоты наклон изменяется на +20 дБ, если множитель типа  находится в числителе модуля передаточной функции, и изменяется на –20 дБ, если этот множитель находиться в знаменателе. Наклон асимптоты кратен 20 дБ на декаду. По ЛАЧХ можно восстановить частотную передаточную функцию. ЛАЧХ широко используется как при анализе, так и при синтезе.
находится в числителе модуля передаточной функции, и изменяется на –20 дБ, если этот множитель находиться в знаменателе. Наклон асимптоты кратен 20 дБ на декаду. По ЛАЧХ можно восстановить частотную передаточную функцию. ЛАЧХ широко используется как при анализе, так и при синтезе.
Дата добавления: 2018-08-06; просмотров: 773; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
